
16.3 Частицы в бесконечно глубокой потенциальной яме
Потенциальной ямой называется часть пространства, ограниченная участками резкого возрастания потенциальной энергии отталкивания, возникающего в результате взаимодействия данной частицы с какими-то внешними полями.
Рассмотрим частицу в одномерной потенциальной яме (рис. 1).
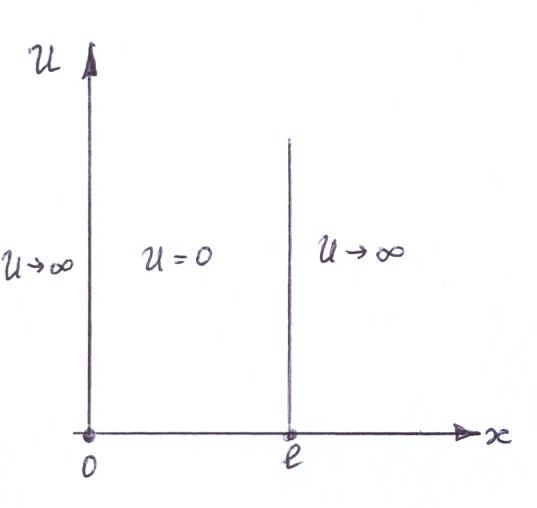
Рис. 1
Потенциальная
энергия
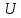 имеет вид:
имеет вид:
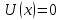 при
при
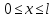 и
и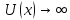 при
при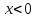 и
и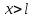 .
.
На стенках потенциальной ямы частица находиться не может, что можно записать в виде условия:
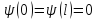 (16.13)
(16.13)
Стационарное
уравнение Шредингера (16.8) для частицы,
находящейся внутри ямы (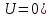 ,
запишем в виде:
,
запишем в виде:
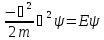
Для
одномерной ямы
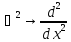 ,
поэтому
,
поэтому
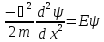
или
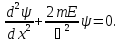 (16.14)
(16.14)
Введя обозначение
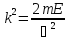 ,
(16.15)
,
(16.15)
придем к уравнению, хорошо известному из теории колебаний:
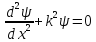 . (16.16)
. (16.16)
Решение такого уравнения имеет вид:
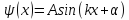 , (16.17)
, (16.17)
где
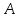 и
и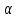 – произвольные постоянные.
– произвольные постоянные.
Из
условия
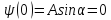 следует, что
следует, что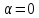 .
.
Из
условия
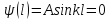 в свою очередь следует, что
в свою очередь следует, что
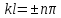 ,
(16.18)
,
(16.18)
где
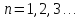 (
(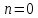 отпадает, так как при этом
отпадает, так как при этом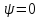 – частица нигде не находится).
– частица нигде не находится).
Подставив
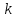 из
(16.18) в (16.15), найдем собственные значения
энергии частицы:
из
(16.18) в (16.15), найдем собственные значения
энергии частицы:
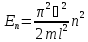 ,
,
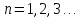 (16.19) Энергия оказалась квантованной и
ее спектр – дискретный (рис. 2).
(16.19) Энергия оказалась квантованной и
ее спектр – дискретный (рис. 2).
Подставив
значение
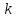 из (16.18) в (16.17), где
из (16.18) в (16.17), где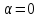 ,
найдем собственные функции:
,
найдем собственные функции:
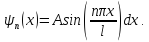
Для определения коэффициента А воспользуемся условием нормировки(16.3). В нашем случае оно примет вид
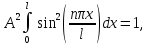
откуда
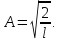
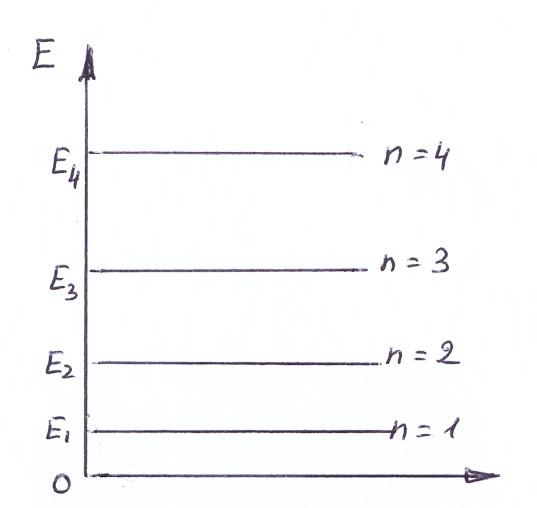
Рис. 2
Таким образом, собственные функции имеют вид:
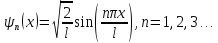 (16.20)
(16.20)
Графики
собственных функций, изображены на рис.
3а. На рис. 3б дана плотность вероятности
обнаружения частицы на различных
расстояниях от стенок ямы, равная
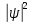 .
.
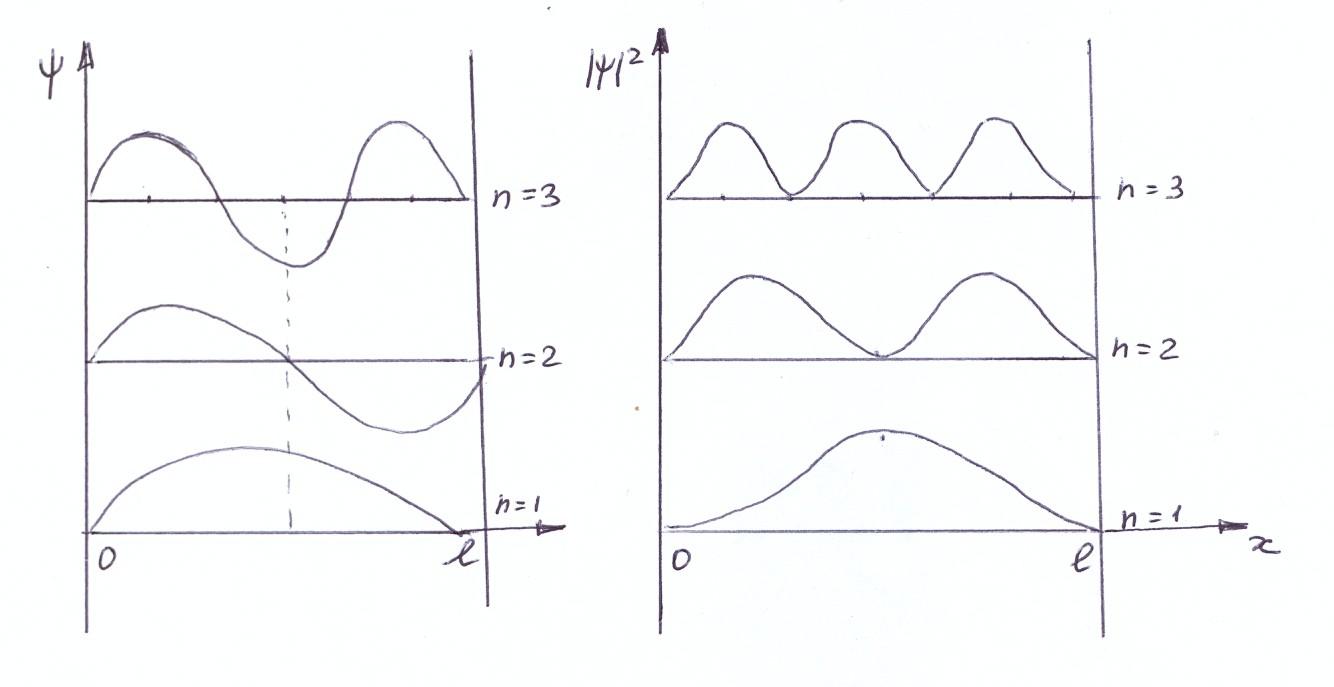
а) б)
Рис. 3
Из
графиков, например, следует, что в
состоянии с
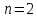 частица не может быть обнаружена в
середине ямы и вместе с тем одинаково
часто бывает как в левой, так и в правой
половине ямы. Такое поведение частицы
резко отличается от поведения классической
частицы, для которой все положения в
яме равновероятны.
частица не может быть обнаружена в
середине ямы и вместе с тем одинаково
часто бывает как в левой, так и в правой
половине ямы. Такое поведение частицы
резко отличается от поведения классической
частицы, для которой все положения в
яме равновероятны.
16.4 Квантовый гармонический осциллятор
Гармоническим
осциллятором называют частицу, совершающую
одномерное движение под действием
квазиупругой силы
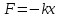 .
.
Потенциальная энергия такой частицы имеет вид:
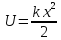 ,
(16.21)
,
(16.21)
Собственная
частота классического гармонического
осциллятора равна
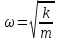 ,
где
,
где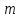 – масса частицы. Выразив
– масса частицы. Выразив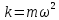 ,
получим
,
получим
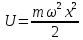 .
(16.22)
.
(16.22)
В
квантовой теории понятие силы теряет
смысл, поэтому квантовый гармонический
осциллятор следует определить как
поведение частицы массы
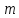 с потенциальной энергией
с потенциальной энергией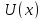 такой же, как у классического осциллятора
(см. формулу (16.22)).
такой же, как у классического осциллятора
(см. формулу (16.22)).
Графиком
функции
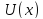 является параболическая яма (рис. 4).
является параболическая яма (рис. 4).
В
одномерном случае
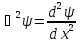 .
Поэтому уравнение Шредингера (16.8) для
осциллятора будет иметь вид:
.
Поэтому уравнение Шредингера (16.8) для
осциллятора будет иметь вид:
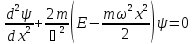 (16.23)
(16.23)
Нахождение
решения этого уравнения, т.е. -функции,
является громоздкой математической
задачей. Для нас главное не в этом.
Оказывается, уравнение (16.23) имеет
конечные, однозначные, непрерывные и
гладкие решения (собственные функции)
при собственных значениях
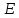 ,
равных
,
равных
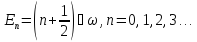 (16.24)
(16.24)
На рис. 4 дана схема энергетических уровней гармонического осциллятора. Для наглядности уровни вписаны в кривую потенциальной энергии.
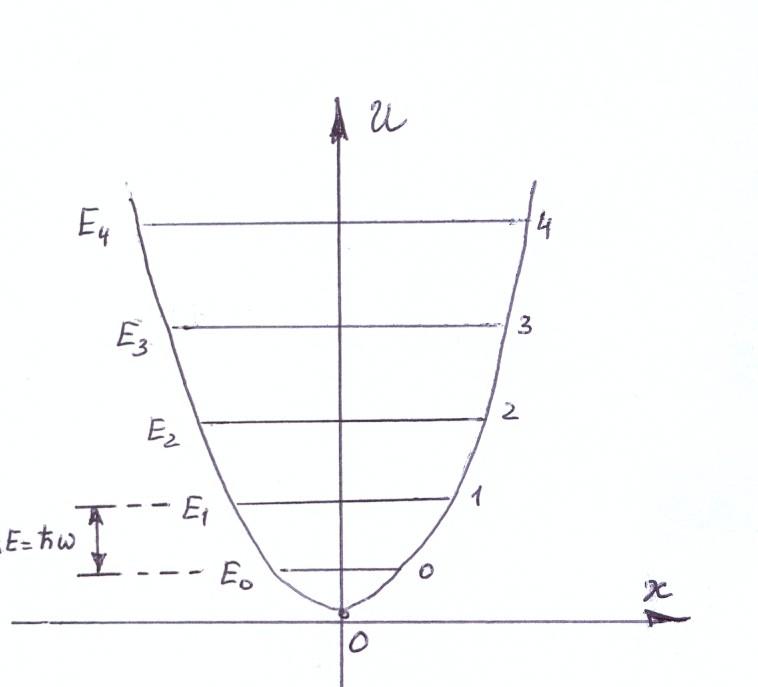
Рис. 4
Видно,
что эти уровни – эквидистантны, т.е.
отстоят друг от друга на одинаковом
расстоянии
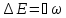 .
Минимальная энергия
.
Минимальная энергия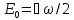 ,
ее называют нулевой энергией. Так как
основной уровень
,
ее называют нулевой энергией. Так как
основной уровень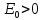 ,
то квантовый осциллятор остановить
нельзя. Например, из-за этого даже при
температуре абсолютного нуля не
прекращаются колебания атомов в
кристаллической решетке.
,
то квантовый осциллятор остановить
нельзя. Например, из-за этого даже при
температуре абсолютного нуля не
прекращаются колебания атомов в
кристаллической решетке.
Квантовая механика позволяет вычислить вероятности различных переходов квантовой системы из одного состояния в другое.
Подобные
вычисления показывают, что для квантового
осциллятора возможны переходы между
соседними уровнями. При таких переходах
квантовое число
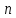 изменяется на единицу:
изменяется на единицу:
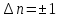 .
(16.25)
.
(16.25)
Условия,
накладываемые на изменения квантовых
чисел при переходах системы из одного
состояния в другое, называются правилами
отбора.
Таким образом, для гармонического
осциллятора существует правило отбора,
выражаемое формулой (16.25). Из этого
условия вытекает, что энергия гармонического
осциллятора может изменяться только
порциями
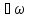 .
.
Понятие о квантовом осцилляторе играет важную роль в теории колебаний атомов в молекулах, а также в теории колебаний атомов в узлах кристаллической решетки твердого тела.
