Модуль 23

Глава 16 Элементы квантовой механики

16.1 Состояние частицы в квантовой механике

Для микрочастиц из-за соотношения неопределенностей классическое определение состояния частиц (координаты и импульс) утрачивает смысл. В соответствии с двойственной природой частиц в квантовой теории состояние частицы задается пси-функцией , которая является комплексной величиной, определяемой во всех точках пространства и в каждый момент времени.

Правильную интерпретацию пси-функции дал М. Борн в 1926 г. Согласно Борну квадрат модуля пси-функции определяет вероятностьтого, что частица будет обнаружена в пределах объема:

(16.1)

Отсюда плотность вероятности, то есть вероятность нахождения частицы в единице объема, равна

. (16.2)

Плотность вероятности является экспериментально наблюдаемой величиной, в то время как сама пси-функция, будучи комплексной, не доступна наблюдению. Пси-функцию выбирают так, чтобы она удовлетворяла условию нормировки:

, (16.3)

где интеграл берется по всему пространству.

Функции, удовлетворяющие этому условию, называются нормированными. Этот интеграл дает вероятность того, что частица находится в одной из точек пространства, то есть вероятность достоверного события равна 1.

Таким образом, физический смысл имеет не сама функция , а квадрат ее модуля.

16.2 Уравнение Шредингера. Квантование энергии

Уравнение движения квантовой нерелятивистской частицы в силовом поле называется уравнением Шредингера, так как впервые было сформулировано Э. Шредингером в 1926 г. Справедливость этого уравнения установлена тем, что все вытекающие из него следствия подтверждены экспериментом. Данное уравнение было открыто на “кончике пера”, оно является новым фундаментальным законом, играет в квантовой механике такую же роль, как уравнение Ньютона в классической физике.

Уравнение Шредингера имеет следующий вид:

, (16.4)

где – масса частицы,– мнимая единица,– потенциальная энергия частицы в силовом поле (мы ограничимся рассмотрением потенциальных силовых полей, для которых функцияне зависит явно от времени),- оператор Лапласа, результат действия которого на некоторую функцию представляет собой

. . (16.5)

В одномерном случае уравнение Шредингера имеет вид:

. (16.6)

Из-за присутствия в уравнении Шредингера мнимой единицы волновые функции, удовлетворяющие этому уравнению, всегда комплексны. Поэтому сами эти функции не наблюдаемы. Измеримы только квантовомеханические вероятности .

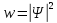Стационарные состояния. Среди решений уравнения Шредингера есть стационарные. Так называются состояния, в которых ни одна из квантовомеханических вероятностей не изменяется со временем, то есть сохраняется. Согласно этому определению в каждом стационарном состоянии средние значения всех физических величин от времени не зависят. В частности, среднее значение координаты

(16.7)

оказывается постоянным во времени.

Если частица движется в стационарном силовом поле, то есть в поле , не зависящем от времени, тогда удается выделить явную зависимость волновой функции от времени. Можно в уравнении (16.4) произвести разделение переменныхи. Для этого будем искать решение в виде:

,

где – координатная часть волновой функции,– временная часть.

После подстановки в (16.4) получим

.

Поделив на , имеем

.

Так как в левой части стоят слагаемые, зависящие только о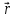т , а правая часть зависит только от, то равенство этих частей возможно лишь в том случае, если обе его части равны одной и той же константе. Очевидно, что константа, равная, имеет размерность энергии, как и величина.

Таким образом, мы получаем два уравнения:

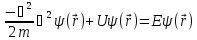(16.8)

– стационарное уравнение Шредингера для функции ,

(16.9)

–уравнение для функции

Решая уравнение (16.9), получим

,

положив , будем иметь

.

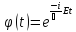Таким образом, полная волновая функция в стационарных состояниях имеет вид:

. (16.10)

Здесь – полная энергия частицы, которая сохраняется во времени, то есть в случае стационарного поля остается постоянной.

При таком виде Ψ-функции плотность вероятности остается постоянной. В самом деле,

, (16.11)

то есть действительно плотность вероятности от времени не зависит.

По этой причине состояния, описываемые Ψ-функциями вида (16.10), называются стационарными.

Квантование энергии. Волновая функция, для того чтобы определять собой плотность вероятности обнаружения частицы, должна удовлетворять стандартным условиям. Эти условия состоят в том, что пси-функция должна быть однозначной, конечной, непрерывной и гладкой (то есть без изломов) во всем пространстве, даже в тех точках, где потенциальная энергиятерпит разрыв. Это обычные требования, накладываемые на искомое решение дифференциального уравнения (16.8).

Решения, удовлетворяющие этим условиям, оказываются возможными лишь при некоторых значениях энергии . Их называютсобственными значениями, а функции 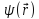, являющиеся решениями уравнения (16.8) при этих значениях энергии, называютсясобственными функциями.

Совокупность собственных значений называется энергетическим спектром.

Если эта совокупность образует дискретную последовательность, спектр называется дискретным, т.е. говорят, что энергия квантуется. Если собственные значения образуют непрерывную последовательность, спектр называют непрерывным или сплошным.

В случае дискретного спектра собственные значения и собственные функции можно пронумеровать:

, (16.12)

.

В этом и состоит естественный и общий принцип квантования.

Теперь перейдем к рассмотрению нескольких простейших задач.