
- •Раздел IV.
- •Основные понятия и зависимости.
- •Кручение стержней круглого и кольцевого поперечных сечений
- •Кручение некруглых стержней
- •Потенциальная энергия деформации при кручении
- •Задача №1
- •Выразим полярный момент сопротивления сечения:
- •Максимальные касательные напряжения в сечениях вала:
- •Задача №2
- •Построение эпюры крутящих моментов (см. Рис.4)
- •4). Максимальные напряжения, действующие в сечениях вала.
Максимальные касательные напряжения в сечениях вала:
![]() МПа.
– что значительно меньше допускаемого.
МПа.
– что значительно меньше допускаемого.
Распределение напряжений по поперечному сечению вала рис.6

рис.6
6).
Определим углы закручивания сечений
(относительно левого шкива, условно
считая его закрепленным) по формуле -
![]() :
:
![]() рад;
рад;
![]() рад;
рад;
![]() рад.
рад.
Эпюра углов закручивания вместе с эпюрой крутящих моментов представлены на рис.7.
7). Определение потенциальной энергии упругой деформации вала по формулам -
U=U1+U2+U,
![]() [н·М]:
[н·М]:
U1= 0.5Mкр11 = 0.5127.3(-0.002) = 0.127 Нм
U2= 0.5Mкр22 = 0.5127.30.002 = 0.127 Нм
U3= 0.5Mкр33 = 0.542.40.004 = 0.085 Нм
U=U1+U2+U3 = 0.127+0.127+0.085 = 0.085 Нм.

рис.7
Задача №2
Условие задачи: Для заданного ступенчатого вала (см. рис.1), жестко защемленного по концам и нагруженного внешними крутящими моментами: раскрыть статическую неопределимость; рассчитать допустимую внешнюю нагрузку из условия прочности; построить эпюры крутящего момента и углов закручивания.
Исходные данные: a = 100 мм; h = b; d = b; b = 35 мм; m1 = m; m2 = 2m; d/D = 0.8; [] = 1 град/м. Материал вала - чугун СЧ 21-40, с пределами прочности: вр = 210МПа – на растяжение; вс = 1000МПа – на сжатие и модулем сдвига G = 50000 МПа. Коэффициент запаса прочности – n = 2.

рис.1
Решение:
1). Определим допускаемые касательные напряжения для материала вала используя известную для хрупких материалов зависимость: []=(0.6...0.7)[]. Допускаемые нормальные напряжения [] = вр/n = 210/2 = 105 МПа. Тогда: []=0.67105 = 70 МПа.
2).
Система является один раз статически
неопределимой (см. рис.2), так как в
заделках А
и В
возникают два реактивных момента mA
и mD,
а для их определения имеется всего одно
уравнение статики:
![]() .
.
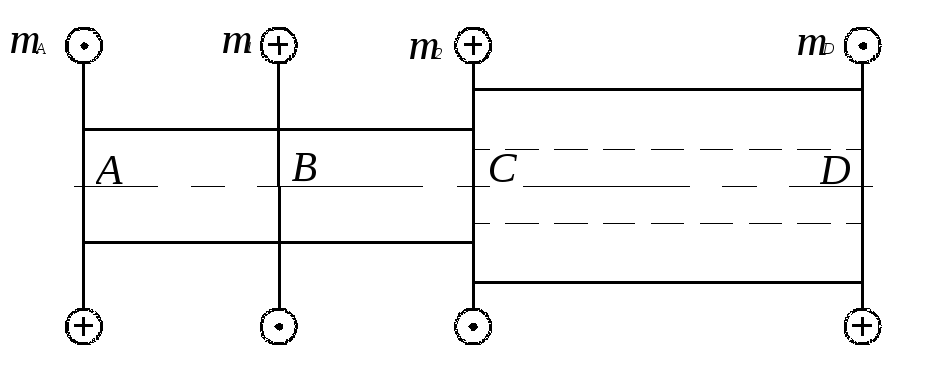
рис.2
Следовательно, сначала необходимо раскрыть статическую неопределимость.
Для
раскрытия статической неопределимости
отбрасываем сначала левую заделку и ее
действие на вал заменяем моментом mA
(см. рис.3). Дополнительное условие для
определения mA
(условие
совместности деформации)
можно сформулировать следующим образом:
поворот левого торцевого сечения
относительно правого равен нулю:
![]() .
.

рис.3
Угол
поворота сечения А
может быть
выражен как алгебраическая сумма
взаимных углов поворота торцевых сечений
на участках AB,
BC, CD:
![]() .
Используя метод сечений выразим крутящие
моменты на участках:
.
Используя метод сечений выразим крутящие
моменты на участках:![]() - крутящий момент на участкеАВ;
- крутящий момент на участкеАВ;
![]() - крутящий момент на участкеВС;
- крутящий момент на участкеВС;
![]() - крутящий момент на участкеСD.
- крутящий момент на участкеСD.
Учитывая, что m1 = m, а m2 = 2m, можно записать:
![]() ,
где I1
и I2
- соответственно моменты инерции
прямоугольного и кольцевого сечений.
,
где I1
и I2
- соответственно моменты инерции
прямоугольного и кольцевого сечений.
Выполняя
элементарные преобразования получим:
![]() .
.
Для
прямоугольного сечения
![]() ,
учитывая, что для
,
учитывая, что для![]() коэффициент
коэффициент![]() получим
получим
![]() .
.
Для
кольцевого сечения ![]() мм4, где
мм4, где
![]() .
.
Подставляя моменты инерции в уравнение совместности деформации получим:
![]()
![]() откуда
откуда
![]() mА=1.748m.
mА=1.748m.
Момент в правой заделке mDнайдем из условия статикиmD= m + 2m – mA mA = 3m - 1.748m mD = 1.252m.
Построение эпюры крутящих моментов (см. Рис.4)
MАВ= ma = 1.748m
MBC= ma+m1 = 1.748m+m = 0.748m
MCD=ma+m1+m2 = 1.748m+m+2m = 1.252m
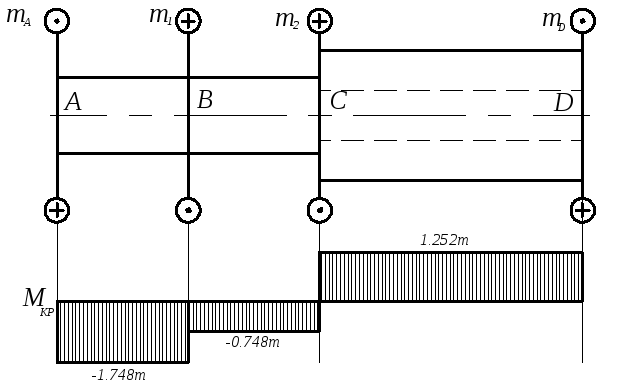
рис.4
3). Определим допускаемое значения внешней нагрузки из условия прочности.
Рассчитаем моменты сопротивления кручению поперечных сечений вала:
прямоугольное сечение -
 ,
учитывая, что для
,
учитывая, что для коэффициент
коэффициент
 получим
получим ;
;кольцевое сечение -
 .
.
Опасным
с точки зрения прочности будет участок
вала с прямоугольным поперечным сечением
у которого наибольший по модулю крутящий
момент т.е. участок АВ,
записывая для него условие прочности
![]() найдем допускаемую величину внешнего
момента
найдем допускаемую величину внешнего
момента![]() .
.
Из
условия прочности для участка СD с
кольцевым поперечным сечением:![]() снова найдем допускаемую величину
внешнего момента
снова найдем допускаемую величину
внешнего момента
![]() .
.
Так как
условия прочности должны выполнятся
для всех участков вала то в качестве
допускаемой внешней нагрузки необходимо
выбрать наименьшее из полученных
значений -
![]() .
.
