Эмпирическая функция распределения
Пусть
известно статистическое распределение
признака
![]() ,
т.е. построен вариационный ряд для
выборки объема
,
т.е. построен вариационный ряд для
выборки объема![]() .
Пусть
.
Пусть![]() –число
вариант, приходящихся на интервал
–число
вариант, приходящихся на интервал![]() .
Относительная частота события
.
Относительная частота события![]() равна
равна![]() .
.
Эмпирической
функцией распределения (функцией
распределения выборки) называется
функция
![]() ,
определяющая для каждого значения
,
определяющая для каждого значения![]() относительную частоту события
относительную частоту события![]() ,
т.е.
,
т.е.![]() .
Из теоремы Бернулли следует, что
относительная частота события
.
Из теоремы Бернулли следует, что
относительная частота события![]() ,
т.е.
,
т.е.![]() ,
стремится по вероятности к вероятности
этого события:
,
стремится по вероятности к вероятности
этого события:![]() для любого
для любого![]() .
Это означает, что функции
.
Это означает, что функции![]() и
и![]() мало отличаются друг от друга при больших
значениях
мало отличаются друг от друга при больших
значениях![]() .
.
Функция
![]() обладает всеми свойствами функции
обладает всеми свойствами функции![]() .:
.:
1)
![]() ,
2)
,
2)![]() –
неубывающая функция, 3)
–
неубывающая функция, 3)![]() при
при![]() ,
,![]() при
при![]() .
Эмпирическая функция распределения
приближенно представляет собой
теоретическую функцию распределения.
.
Эмпирическая функция распределения
приближенно представляет собой
теоретическую функцию распределения.
В примере 1
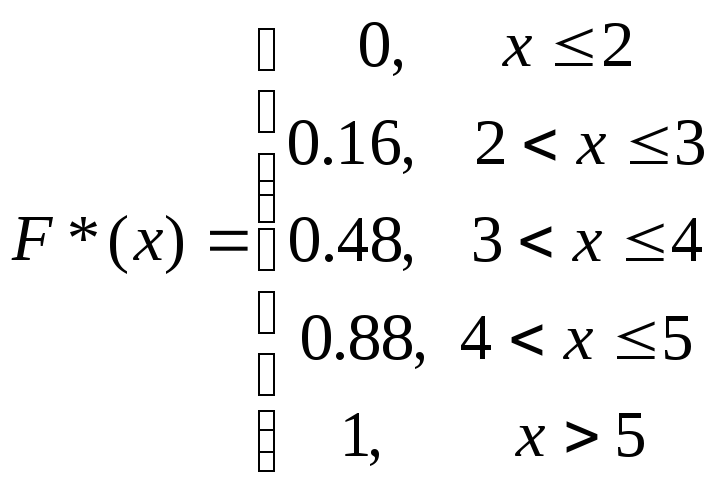 .
.
Статистические оценки параметров распределения
Наиболее существенными параметрами распределения являются математическое ожидание и дисперсия распределения. Статистические оценки параметров распределения называются статистиками.
Статистической оценкой математического ожидания является среднее арифметическое или среднее выборочное
![]() .,
(1)
.,
(1)
где
![]() ,
,![]() ,
,![]() .
(2)
.
(2)
Свойства среднего арифметического
1)
![]()
Действительно,
![]() .
.
2)
![]() .
.
![]() .
.
3) Сумма отклонений всех вариант от их среднего арифметического равна нулю:
![]()
4) Сумма квадратов отклонений вариант от их среднего арифметического меньше суммы квадратов их отклонений от любого другого числа
![]()
Доказательство
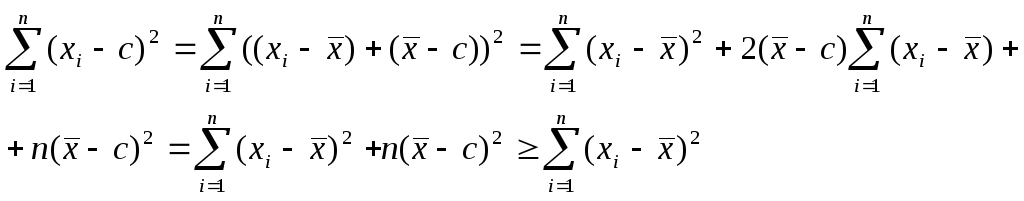
При
выводе этого соотношения было учтено
равенство
![]() =0
и неравенство
=0
и неравенство![]() .
.
Медиана
или срединное значение
![]() –
значение признака, для которого
накопленная относительная частота
равна 0.5. При наличии сгруппированных
данных для отыскания медианы нужно
определить интервал, для нижней границы
которого значение накопленной
относительной частоты меньше 0.5, а для
верхней границы больше 0.5. Середина
этого интервала принимается за медиану.
–
значение признака, для которого
накопленная относительная частота
равна 0.5. При наличии сгруппированных
данных для отыскания медианы нужно
определить интервал, для нижней границы
которого значение накопленной
относительной частоты меньше 0.5, а для
верхней границы больше 0.5. Середина
этого интервала принимается за медиану.
Мода
![]() –
значение признака, соответствующее
максимуму теоретической кривой. За моду
принимают середину модального интервала
– интервала с наибольшей частотой.
Мода– абсцисса наивысшей точки полигона.
Модальный интервал соответствует
наивысшей ступени гистограммы.
–
значение признака, соответствующее
максимуму теоретической кривой. За моду
принимают середину модального интервала
– интервала с наибольшей частотой.
Мода– абсцисса наивысшей точки полигона.
Модальный интервал соответствует
наивысшей ступени гистограммы.
Пример
1.
![]() –средняя оценка на экзамене.
–средняя оценка на экзамене.
![]() ,
,![]()
Пример
2.
![]() . Модальный интервал[115;120].
. Модальный интервал[115;120].
![]()
![]() .
.
Статистическая дисперсия
В качестве меры разброса вариант относительно среднего значения вводят статистическую дисперсию
![]() .
(3)
.
(3)
Вообще
говоря, статистическую дисперсию нужно
вводить как сумму квадратов отклонений
вариант от математического ожидания
![]() случайной
величины, т.е.
случайной
величины, т.е.
![]() (4)
(4)
Но
поскольку
![]() неизвестно, то в качестве статистической
дисперсии используют определение (3).
Однако при этом происходит занижение
оценки дисперсии, т.е. статистическая
дисперсия является смещенной оценкой
дисперсии генеральной совокупности.
Для исправления этой ошибки нужно в
формуле (3) заменить
неизвестно, то в качестве статистической
дисперсии используют определение (3).
Однако при этом происходит занижение
оценки дисперсии, т.е. статистическая
дисперсия является смещенной оценкой
дисперсии генеральной совокупности.
Для исправления этой ошибки нужно в
формуле (3) заменить![]() на
на![]() .
Поэтому для оценки дисперсии генеральной
совокупности используютисправленную
статистическую дисперсию
.
Поэтому для оценки дисперсии генеральной
совокупности используютисправленную
статистическую дисперсию
![]() ,
(5)
,
(5)
которая
является несмещенной оценкой
дисперсии генеральной совокупности.
Если
![]() велико, то формулы (3) и (5) дают практически
один и тот же результат. В случае
велико, то формулы (3) и (5) дают практически
один и тот же результат. В случае![]() для вычисления статистической дисперсии
используют формулу (5).
для вычисления статистической дисперсии
используют формулу (5).
Статистическое среднеквадратичное отклонение (СКВО)
![]() (6)
(6)
Коэффициентом вариации признака называется
![]() .
(7)
.
(7)
Свойства статистической дисперсии и статистического СКВО.
1)
![]() для постоянной величины
для постоянной величины![]() .
.
2)
![]() .
.
Доказательство.
![]() .
.
3)
![]()
Доказательство
![]()
4)
![]() (8)
(8)
Доказательство.
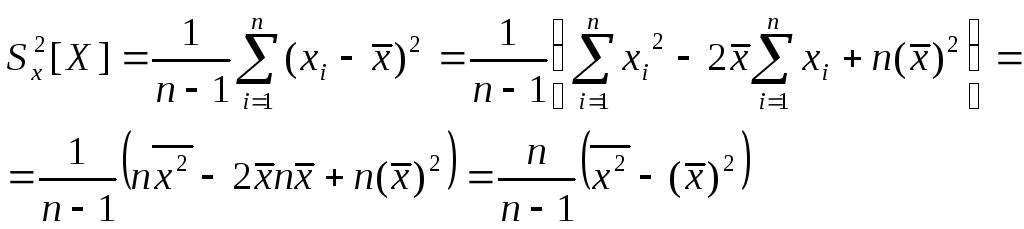
Формулу (8) используют для практического вычисления дисперсии.
Пример2.
![]()
![]() ,
,
![]() .
.
![]() Выборочная
асимметрия
Выборочная
асимметрия ![]() и
выборочный
эксцесс
и
выборочный
эксцесс
![]() определяются
соотношениями
определяются
соотношениями
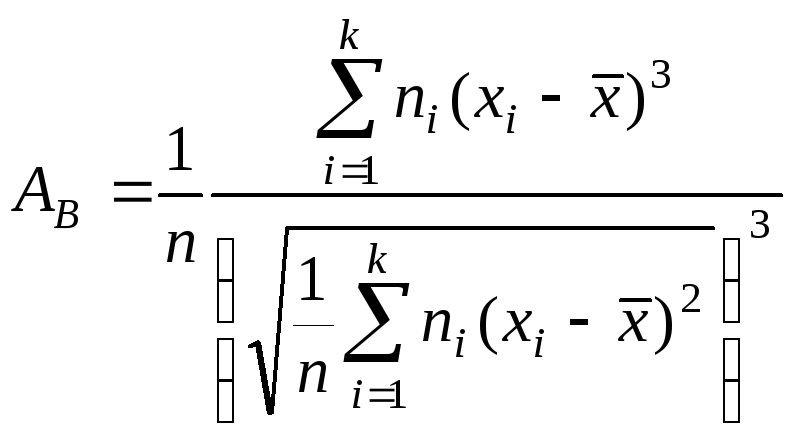 ,
,