
- •Лекция 2 Несмещенные, эффективные и состоятельные оценки параметров распределения
- •Интервальные оценки параметров распределения
- •Интервальные оценки математического ожидания
- •Задача о надежности определения математического ожидания при заданной точности
- •2. Задача о точности оценки математического ожидания при заданной надежности
- •3. Планирование числа испытаний.
- •Интервальная оценка дисперсии
- •Выравнивание статистических рядов
- •Критерий согласия Пирсона
- •Критерий согласия Колмогорова или критерий
- •Критерий Романовского
2. Задача о точности оценки математического ожидания при заданной надежности
Пусть
имеется выборка выборка объема
![]() .
Величина
.
Величина![]() – среднее арифметическое. Нужно найти
такой промежуток
– среднее арифметическое. Нужно найти
такой промежуток![]() ,
относительно которого с заданной
вероятностью
,
относительно которого с заданной
вероятностью![]() можно утверждать, что
можно утверждать, что![]() .
Задача решается так же, как и в предыдущем
случае. При больших значениях
.
Задача решается так же, как и в предыдущем
случае. При больших значениях![]() нужно использовать нормальное
распределение, а при малых значениях
нужно использовать нормальное
распределение, а при малых значениях![]() – распределение Стьюдента.
– распределение Стьюдента.
Пример
3.
На токарном станке изготовлена большая
партия валиков. Измерены отклонения
диаметров 16 случайно отобранных из этой
партии валиков от середины поля допуска.
Среднее значение измеренных отклонений
равно 2 мк, статистическая дисперсия
![]() ,
,![]() .
Найти промежуток
.
Найти промежуток![]() ,
относительно которого можно утверждать
с вероятностью
,
относительно которого можно утверждать
с вероятностью![]() ,
что среднее значение отклонения
диаметров валиков всей партии заключено
в этом промежутке.
,
что среднее значение отклонения
диаметров валиков всей партии заключено
в этом промежутке.
Решение.
![]() .
Нужно найти
.
Нужно найти![]() .
Применим распределение Стьюдента.
.
Применим распределение Стьюдента.![]() ,
,![]() Из таблицы значений
Из таблицы значений![]() =0.9
найдем
=0.9
найдем![]() .
Учитывая, что
.
Учитывая, что![]() ,
получим
,
получим![]() .
Отсюда
.
Отсюда![]() .
Следовательно, с надежностью 0.9 можно
утверждать, что среднее значение
отклонения диаметров валиков всей
партии от середины поля допуска заключено
между 1 мк и 3 мк.
.
Следовательно, с надежностью 0.9 можно
утверждать, что среднее значение
отклонения диаметров валиков всей
партии от середины поля допуска заключено
между 1 мк и 3 мк.
С
помощью нормального распределения
получим
![]() .
Отсюда с помощью таблиц функции Лапласа
найдем
.
Отсюда с помощью таблиц функции Лапласа
найдем![]() и следовательно
и следовательно![]() .
.
Надежность 0.9 указывает, что если произведено достаточно большое число выборок, то 90% из них определяет такие доверительные интервалы, в которых параметр действительно заключен и лишь в 10% случаев он может выйти за границы доверительного интервала.
3. Планирование числа испытаний.
Сколько
наблюдений над случайной величиной
нужно произвести для того, чтобы с
заданной вероятностью
![]() можно было утверждать, что отклонение
можно было утверждать, что отклонение![]() не превзойдет заданного числа
не превзойдет заданного числа![]() при заданной дисперсии.
при заданной дисперсии.
В
этом случае заданы
![]() и
и![]() .
По таблице из равенства
.
По таблице из равенства![]() находим значение аргумента
находим значение аргумента![]() и затем решаем неравенство
и затем решаем неравенство![]() относительно
относительно![]() :
:![]() .
.
Пример 4. СКВО измерения глубины моря равно 30 м. Сколько надо сделать промеров, чтобы определить глубину моря с ошибкой не более 20м, если надежность этого заключения должна быть не меньше 0.9?
Решение.
![]() .
.![]() .
Из таблицы находим
.
Из таблицы находим![]() .
Отсюда
.
Отсюда![]() и
и![]()
Интервальная оценка дисперсии
Иногда
приходится оценивать неизвестную
дисперсию случайной величины по
статистической дисперсии выборки
![]() .
.
Пусть
С.В. распределена нормально. Зададим
промежуток
![]() и найдем вероятность того, что СКВО
попадет в интервал
и найдем вероятность того, что СКВО
попадет в интервал![]() ,
т.е.
,
т.е.![]() .
Введем в рассмотрение случайную величину
.
Введем в рассмотрение случайную величину![]() .
Известно, что
.
Известно, что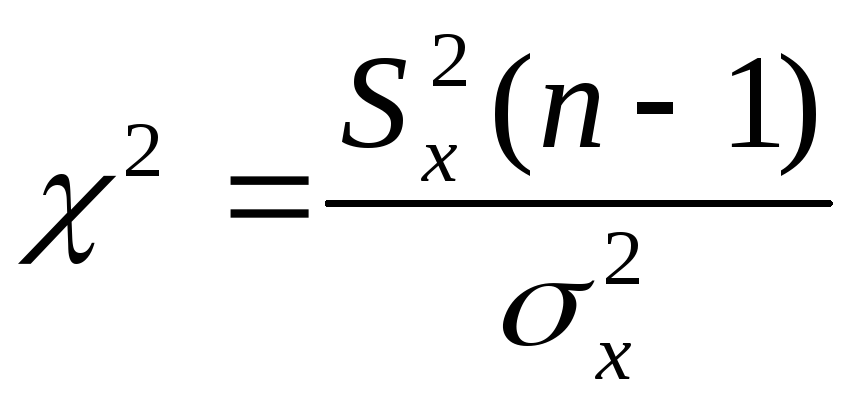 распределена по закону
распределена по закону![]() с
с![]() степенями свободы. Плотность распределения
величины
степенями свободы. Плотность распределения
величины![]()
равна
![]() .
.
Преобразуем неравенство
![]() (14)
(14)
так,
чтобы оно приняло вид
![]() .
Из (14) получим
.
Из (14) получим
![]() ,
отсюда
,
отсюда
![]() .
.
Введем
обозначение
![]() .
Тогда неравенство можно переписать в
виде
.
Тогда неравенство можно переписать в
виде![]() ,
что равносильно неравенству
,
что равносильно неравенству![]() .
Следовательно,
.
Следовательно,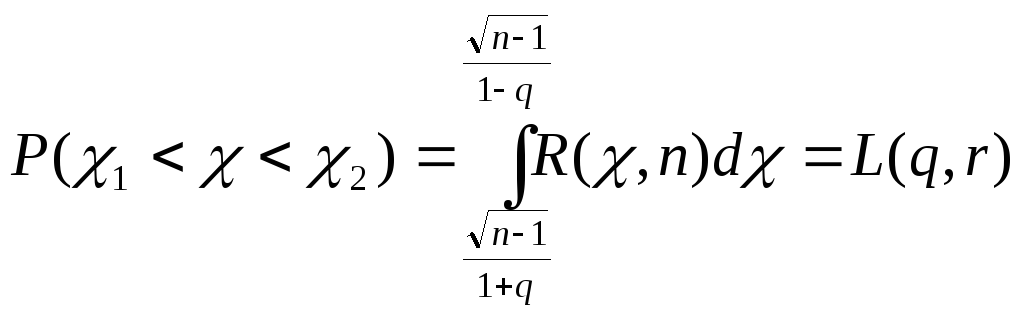 ,
где
,
где![]() .
.
Функция
![]() )табулирована.
По заданной доверительной вероятности
и числу степеней свободы из таблиц можно
найти
)табулирована.
По заданной доверительной вероятности
и числу степеней свободы из таблиц можно
найти
![]() ,
а затем найти доверительный интервал
,
а затем найти доверительный интервал![]() для неизвестного СКВО
для неизвестного СКВО![]() .
Можно решить и обратную задачу: по
заданному доверительному интервалу
найти доверительную вероятность.
.
Можно решить и обратную задачу: по
заданному доверительному интервалу
найти доверительную вероятность.
Пример
5. Произведено
10 наблюдений над случайной величиной
![]() ,
распределенной нормально. Статистическое
СКВО
,
распределенной нормально. Статистическое
СКВО![]() .
С какой вероятностью можно утверждать,
что заключено между 5 и 7?
.
С какой вероятностью можно утверждать,
что заключено между 5 и 7?
Решение.
Здесь
![]() ,
,![]() ,
,![]() .
.![]()
В
теории ошибок точность измерений
характеризуют с помощью среднего
квадратичного отклонения
![]() случайных ошибок измерения.
случайных ошибок измерения.
