ФИЗИКА

Модуль 1.3

Глава 3 Механическая энергия и работа. Закон сохранения энергии

1 Работа и мощность

Пусть частица под действием силы совершает перемещение по некоторой траектории 1-2 (рис. 1).

Рис. 1

Элементарной работой силы на перемещенииназывается скалярное произведение.

Итак,

(3.1)

где - угол между векторамии,- элементарный путь,- проекция векторана вектор.

Суммируя (интегрируя) выражение (3.1) на участке от точки 1 до точки 2, находим работу силы на данном пути:

(3.2)

В выражении (3.2) под (или) следует понимать перемещение точки приложения силы.

Рассмотрим несколько примеров на вычисление работы

1. Работа упругой силы

Работа упругой силы , где- радиус-вектор частицыотносительно точки(рис. 2).

Элементарная работа

Рис. 2

Скалярное произведение

и.

. (3.3)

2. Работа гравитационной (или кулоновской) силы

Пусть в точке (рис.3) находится неподвижный силовой центр – материальная точка, действующая на частицус силой, которая как для гравитационного, так и для кулоновского взаимодействий может быть представлена в виде:

,

где для гравитационной силы,для кулоновской силы,- расстояние от точкидо частицы,- орт радиус-вектора.

О

Рис. 3

Элементарная работа этой силы на перемещении

, где,

поэтому .

Работа этой силы на всем пути от точки 1 до точки 2

. (3.4)

3. Работа однородной силы тяжести

Запишем эту силу в виде , где- орт вертикальной оси(рис. 4).

Рис. 4

Элементарная работа силы тяжести на перемещении

.

Скалярное произведение , поэтому

.

Работа данной силы на всем пути от точки 1 до точки 2

.

Полагая ,, получим

. (3.5)

Вывод: рассмотренные силы интересны в том отношении, что их работа, как видно из (3.3) – (3.5), не зависит от формы пути между точками 1 и 2, а зависит только от положения этих точек. Таким свойством обладают не все силы. Например, сила трения этим свойством не обладает: работа этой силы зависит не только от положения начальной и конечной точек, но и от формы пути между ними.

Единицей измерения работы в СИ является джоуль (Дж).

= 1 Дж = 1 Н·м.

Мощность

Работа, совершаемая в единицу времени, называется мощностью. Мощностьопределяется соотношением

. (3.6)

Учитывая, что ,, получим

. (3.7)

Таким образом, мощность равна скалярному произведению силы на скорость точки приложения силы.

Единицей мощности в СИ является ватт (Вт).

.

2 Консервативные силы. Потенциальная энергия

Консервативные силы

Если в каждой точке пространства на помещенную туда частицу действует сила, то частица находится в поле сил. Так, например, частица может находиться в поле сил тяжести, в поле сил сопротивления.

Поле, остающееся постоянным во времени, называют стационарным. В стационарном силовом поле сила, действующая на частицу, зависит только от ее положения.

Силы, работа которых не зависит от пути, по которому двигалась частица, а зависит лишь от начального и конечного положений частицы, называют консервативными(илипотенциальными).

Работа консервативных сил на любом замкнутом пути равна нулю. Примером являются силы гравитационные, кулоновские, упругие, сила тяжести.

К числу неконсервативных сил относятся, например, силы трения и сопротивления. Работа этих сил зависит, вообще говоря, от пути между начальным и конечным положениями частицы (и не равна нулю на любом замкнутом пути).

Поле, в любой точке которого направление силы, действующей на частицу, проходит через неподвижный центр, а модуль силы зависит только от расстояния до этого центра, называетсяцентральным. Направлена сила либо от центра (как на рис. 5), либо к силовому центру.

Центральную силу можно представить в виде:

. (3.8)

Найдем работу, совершаемую над частицей в центральном стационарном силовом поле.

Элементарная работа силы (3.8) на перемещении есть

,,

- проекция вектора на вектор.

Работа этой силы на всем пути от точки 1 до точки 2

. (3.9)

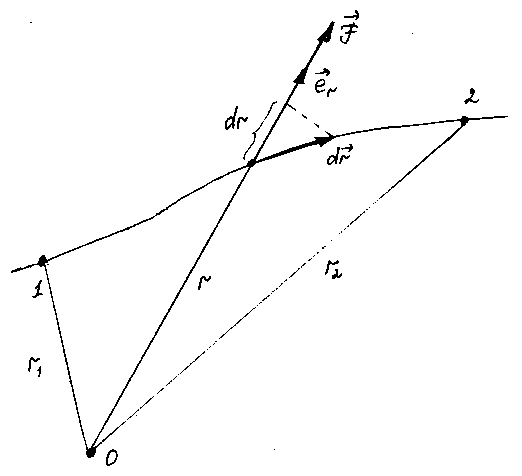
Рис. 5

Это выражение зависит только от вида функции и от значенийи- начального и конечного положения частицы. От формы траектории оно никак не зависит.

Вывод:силы центрального стационарного поля являются консервативными.

Потенциальная энергия частицы в поле

То обстоятельство, что работа консервативных сил в случае стационарного поля зависит только от начального и конечного положения частицы, дает возможность ввести понятие потенциальной энергии. Сопоставим каждой точке поля значение некоторой функции координат .

Работа сил поля при перемещении частицы из точки 1 в точку 2 будет равна разности значений и, которые величинапринимает в точках 1 и 2:

. (3.10)

Величина называется потенциальной энергией частицы в силовом поле.

Таким образом, работа консервативных сил совершается за счет убыли потенциальной энергии частицы в данном поле.

. (3.11)

Равенство (3.10) определяет лишь разность потенциальных энергий в двух точках, саму потенциальную энергию можно определить, если условно принять за нуль значение потенциальной энергии в какой-либо точке пространства.

В предыдущем параграфе мы нашли, что работа силы упругости равна

(см. 3.3). С другой стороны, по формуле (3.10)

Отсюда потенциальная энергия частицы в поле упругой силы

(3.12)

Сопоставление формул (3.4) и (3.10) дает, что потенциальная энергия частицы в гравитационном поле:

, (3.13)

в кулоновском поле:

. (3.14)

Из формул (3.5) и (3.10) следует, что потенциальная энергия частицы в однородном поле сил тяжести

, (3.15)

где отсчитывается от произвольного уровня.

Связь между потенциальной энергией и силой поля

Если известно выражение для потенциальной энергии, можно найти силу, действующую на частицу в каждой точке поля. Пусть частица совершила перемещениепод действием силы, тогда работа этой силы равна

. (3.16)

С другой стороны, согласно формуле (3.11) эта работа равна убыли потенциально энергии:

. (3.17)

Полный дифференциал можно представить в виде:

, (3.18)

где символ частной производной, например, означает, что производная повычисляется при условии, что координатыиостаются постоянными.

Подставляя (3.16) и (3.18) в (3.17), получим

отсюда компоненты силы равны

;;(3.19)

Вектор силы или

(3.20)

Величину, стоящую в скобках, называют градиентом скалярной функции и обозначаютили, где оператор

(3.21)

называется оператором Гамильтонаилиоператором набла.

Таким образом,

, или, (3.22)

т.е. консервативная сила равна градиенту потенциальной энергии частицы в данной точке поля, взятому со знаком минус.