
- •Глава 4 Закон сохранения момента импульса. Механика твердого тела
- •1 Момент силы
- •2 Момент импульса. Закон сохранения момента импульса
- •3 Плоское движение твердого тела
- •4 Вращение твердого тела вокруг неподвижной оси
- •5 Момент инерции. Теорема Штейнера
- •6 Кинетическая энергия вращающегося тела
- •7 Кинетическая энергия тела при плоском движении
6 Кинетическая энергия вращающегося тела
Когда тело вращается вокруг неподвижной
оси с угловой скоростью
![]() ,
элементарная масса
,
элементарная масса![]() ,
отстоящая от оси вращения на расстояние
,
отстоящая от оси вращения на расстояние![]() ,
обладает скоростью
,
обладает скоростью![]() .
Следовательно, ее кинетическая энергия
равна
.
Следовательно, ее кинетическая энергия
равна
![]() .
.
Сумма энергий даст кинетическую энергию всего тела:
![]() ,
,
или
![]() (4.29)
(4.29)
Найдем работу, совершаемую внешними
силами при вращении твердого тела вокруг
неподвижной оси. В соответствии с
уравнением (3.25) работа всех внешних сил,
действующих на твердое тело, равна
приращению кинетической энергии тела.
Таким образом,![]() или, согласно (4.29),
или, согласно (4.29),![]() .
Так как ось
.
Так как ось![]() совпадает
с осью вращения, то
совпадает
с осью вращения, то![]() и
и![]() .
.
Но согласно (4.21),
![]() .
.
Учитывая, что
![]() ,
получаем
,
получаем
![]() (4.30)
(4.30)
Работа внешних сил при повороте тела
на конечный угол
![]() равна
равна
![]() (4.31)
(4.31)
В случае если
![]() ,
то
,
то![]() .
.
7 Кинетическая энергия тела при плоском движении
Представим плоское движение тела как
наложение поступательного движения со
скоростью
![]() некоторой точки
некоторой точки![]() и вращения вокруг оси, проходящей через
эту точку, с угловой скоростью
и вращения вокруг оси, проходящей через
эту точку, с угловой скоростью![]() .
В этом случае скорость
.
В этом случае скорость![]() -той
элементарной массы тела определяется
формулой
-той
элементарной массы тела определяется
формулой
![]() , (4.32)
, (4.32)
где
![]() - радиус-вектор
- радиус-вектор![]() -
той массы, проведенный из точки
-
той массы, проведенный из точки![]() (см. формулу (1.25))
(см. формулу (1.25))
и рис. 11.
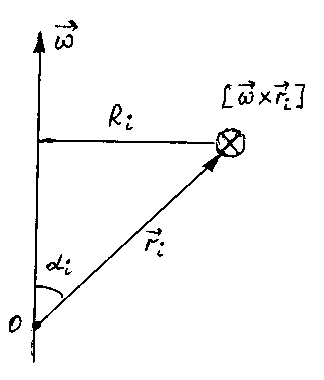
Рис. 11
Кинетическая энергия
![]() -той
элементарной массы равна
-той
элементарной массы равна
![]() .
.
Далее
![]() .
.
Кинетическая энергия равна
![]() .
.
Разобьем полученное выражение на три слагаемых:
![]()
Как следует из рис. 9,
![]() ,
где
,
где![]() - расстояние
- расстояние![]() -той
массы от оси вращения.
-той
массы от оси вращения.
Соответственно третье слагаемое равно
![]() ,
где
,
где![]() -момент
инерции тела относительно оси вращения
-момент
инерции тела относительно оси вращения![]() .
.
Преобразуем второе слагаемое следующим образом:
![]() ,
,
![]() - радиус-вектор центра масс, проведенный
из точки
- радиус-вектор центра масс, проведенный
из точки![]() .
.
Можно записать, что
![]() . (4.33)
. (4.33)
Если в качестве точки
![]() взять центр масс тела
взять центр масс тела![]() ,
то
,
то![]() и формула (4.33) упростится следующим
образом:
и формула (4.33) упростится следующим
образом:
![]() , (4.34)
, (4.34)
где
![]() - скорость центр масс,
- скорость центр масс,![]() - момент инерции тела относительно оси,
проходящей через центр масс.
- момент инерции тела относительно оси,
проходящей через центр масс.
Таким образом, полная кинетическая твердого тела равна сумме кинетической энергии поступательного движения тела со скоростью центра масс и кинетической энергии его вращения относительно оси, проходящей через центр масс.
Задачи
Задача 1Однородный цилиндр массы![]() и радиуса
и радиуса![]() скатывается без скольжения по наклонной
плоскости, составляющей угол
скатывается без скольжения по наклонной
плоскости, составляющей угол![]() с горизонтом (рис.). Найдем уравнения
движения цилиндра.
с горизонтом (рис.). Найдем уравнения
движения цилиндра.
Решение
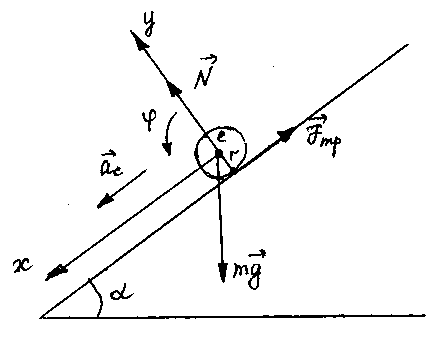
На рис. изображены силы, действующие на тело, и точки их приложения:
![]() - сила тяжести,
- сила тяжести,![]() - сила реакции опоры,
- сила реакции опоры,![]() - сила трения покоя.
- сила трения покоя.
В проекциях на положительные направления
![]() и
и![]() запишем уравнения движения:
запишем уравнения движения:
![]() , (1)
, (1)
![]() , (2)
, (2)
Кроме того, условие отсутствия скольжения определяет связь между ускорениями:
![]() (3)
(3)
Решение трех уравнений дает возможность
найти ускорения
![]() и
и![]() ,
а также силу
,
а также силу![]() .
.
Задача 2 Через блок в виде сплошного
диска, имеющего массу
![]() = 80 г (рис.), перекинута тонкая нерастяжимая
нить, к концам которой подвешены грузы
с массами
= 80 г (рис.), перекинута тонкая нерастяжимая
нить, к концам которой подвешены грузы
с массами![]() = 100 г и
= 100 г и![]() = 200 г. С каким ускорением будут двигаться
грузы, если их предоставить самим себе?
Трением и массой нити пренебречь.
= 200 г. С каким ускорением будут двигаться
грузы, если их предоставить самим себе?
Трением и массой нити пренебречь.
Решение
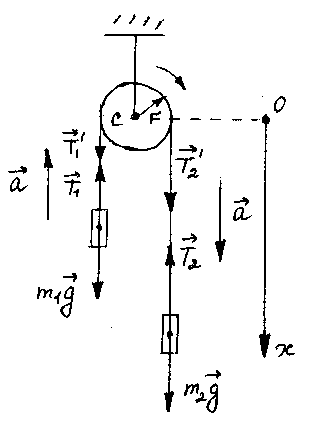
Напишем уравнение движения (второй закон Ньютона) в координатной форме:
![]() :
:![]() (1)
(1)
![]() :
:![]() (2)
(2)
Согласно основному уравнению динамики вращательного движения
![]() , (3)
, (3)
где
![]() - момент инерции блока (сплошного диска)
относительно оси вращения, угловое
ускорение
- момент инерции блока (сплошного диска)
относительно оси вращения, угловое
ускорение![]() .
Согласно третьему закону Ньютона
.
Согласно третьему закону Ньютона![]() ,
,![]() .
Решая систему трех уравнений, получим
.
Решая систему трех уравнений, получим
![]() .
.
Отсюда ускорение равно:
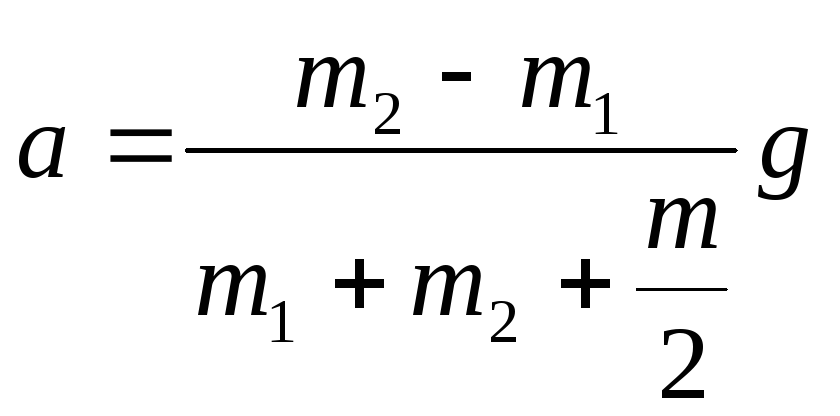 . (4)
. (4)
После подстановки числовых значений, получим
![]() (м/с2)
(м/с2)
Задача 3Маховик в виде сплошного
диска радиусом![]() = 0,2 м и массой
= 0,2 м и массой![]() = 50 кг раскручен до частоты вращения
= 50 кг раскручен до частоты вращения![]() = 480 об/мин и предоставлен самому себе.
Под действием сил трения маховик
остановился через
= 480 об/мин и предоставлен самому себе.
Под действием сил трения маховик
остановился через![]() = 50 с. Найти момент
= 50 с. Найти момент![]() сил трения.
сил трения.
Решение
Работа сил трения равна изменению кинетической энергии диска
![]() ,
,
где
![]() - начальная угловая скорость диска,
- начальная угловая скорость диска,![]() - момент инерции диска,
- момент инерции диска,![]() - угол, на который повернется диск до
остановки при равнозамедленном движении.
- угол, на который повернется диск до
остановки при равнозамедленном движении.
Отсюда
![]() .
.
Произведем вычисления
![]() (Н·м)
(Н·м)
Задача 4 Платформа в виде сплошного
диска радиусом
![]() = 1,5 м и массой
= 1,5 м и массой![]() = 180 кг вращается по инерции около
вертикальной оси с частотой
= 180 кг вращается по инерции около
вертикальной оси с частотой![]() =10
об/мин. В центре платформы стоит человек
массой
=10
об/мин. В центре платформы стоит человек
массой![]() = 60 кг. Какую линейную скорость будет
иметь человек, если он перейдет на край
платформы?
= 60 кг. Какую линейную скорость будет
иметь человек, если он перейдет на край
платформы?
Решение
Платформа вращается по инерции.
Следовательно, момент внешних сил
относительно оси вращения
![]() ,
совпадающей с геометрической осью
платформы равен нулю. При этом момент
импульса
,
совпадающей с геометрической осью
платформы равен нулю. При этом момент
импульса![]() системы платформа – человек остается
постоянным.
системы платформа – человек остается
постоянным.
![]() , (1)
, (1)
где
![]() ,
,![]() - момент инерции платформы,
- момент инерции платформы,![]() - момент инерции человека.
- момент инерции человека.
С учетом этого равенства (1) примет вид:
![]() ,
,
или
![]() , (2)
, (2)
где штрихованные величины относятся к конечному состоянию.
Учитывая, что
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
получим
![]() .
.
Отсюда
![]() .
.
Произведем вычисления
![]() =1
(м/с).
=1
(м/с).
Задача 5С наклонной плоскости
высотой![]() скатываются 1) обруч; 2) сплошной цилиндр;
3) шар. Найти скорости, которые они будут
иметь, скатившись до конца плоскости.
Сравнить эти скорости со скоростью,
которую имело бы тело, соскальзывающее
по плоскости без трения.
скатываются 1) обруч; 2) сплошной цилиндр;
3) шар. Найти скорости, которые они будут
иметь, скатившись до конца плоскости.
Сравнить эти скорости со скоростью,
которую имело бы тело, соскальзывающее
по плоскости без трения.
Решение
Полная кинетическая энергия скатывающегося тела:
![]() .
.
Так как по закону сохранения механической
энергии
![]() или
или![]() ,
то
,
то
![]() ,
,
откуда
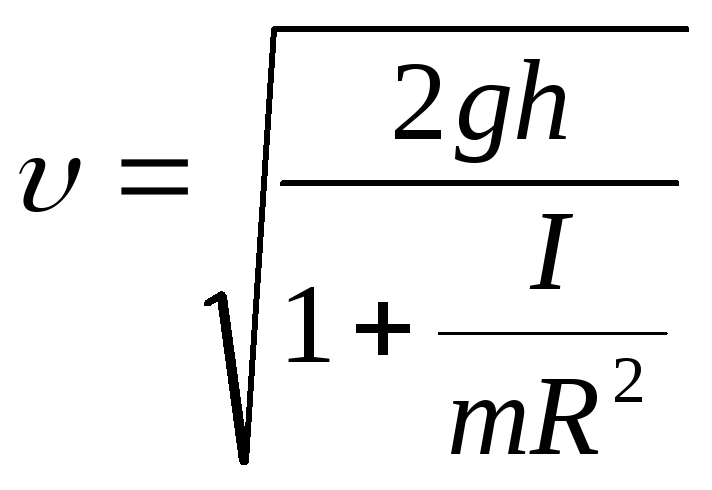
Скорость тела, соскальзывающего без
трения с наклонной плоскости высотой
![]() ,
равна
,
равна
![]()
1) Для обруча
![]() ,
имеем
,
имеем![]() .
.
![]() ,
,![]() .
.
2) Для сплошного цилиндра
![]() ,
откуда
,
откуда![]() .
.
![]() ,
,![]() .
.
3) Для шара
![]() ,
откуда
,
откуда![]() .
.
![]() ,
,![]() .
.
Тесты
1. Единицей измерения модуля момента импульса тела является…
1) …![]() ;
2) …
;
2) …![]() ;
3) …
;
3) …![]() ; 4) …
; 4) …![]() ;
5) …
;
5) …![]() .
.
2. Модуль момента силы в системе СИ измеряют в…
1) …в ньютонах на метр [Н∙м]; 2) …в ньютонах, деленных на метр [Н/м]; 3) …в ньютонах на метр квадратный [H/m2]; 4) …в метрах квадратных [м]; 5) …в ньютонах [Н].
3. Единицей измерения момента инерции тела является…
1) …![]() ;
2) …
;
2) …![]() ;
3) …
;
3) …![]() ;
4) …
;
4) …![]() ;
5) …
;
5) …![]() .
.
4. Дано выражение:
![]() ,
где
,
где![]() -
вектор силы,
-
вектор силы,![]() -
радиус-вектор точки приложения силы.
Это выражение определяет…
-
радиус-вектор точки приложения силы.
Это выражение определяет…
1) …работу силы; 2) …момент силы; 3) …импульс момента силы; 4) …кинетическую энергию точки; 5) …изменение импульса точки.
5. Моментом импульса называется…
1) …![]() ;
2) …
;
2) …![]() ;
3) …
;
3) …![]() ;
4) …
;
4) …![]() ;
5) …
;
5) …![]() .
.
6. В основном законе вращения тела вокруг
неподвижной оси
![]() ;
где
;
где![]() – вектор момента силы,
– вектор момента силы,![]() -
вектор момента импульса,
-
вектор момента импульса,![]() -
время. Как направлены вектора
-
время. Как направлены вектора![]() и
и![]() ?
?
1) …оба перпендикулярно оси вращения и не параллельны друг другу; 2) …взаимно перпендикулярны и каждый перпендикулярен вектору угловой скорости; 3) …вдоль оси вращения в одну сторону; 4) …вдоль оси вращения в противоположные стороны; 5) …оба по касательной к траектории вращающейся точки.
7. Укажите в ответе номер правильного выражения для закона сохранения момента импульса при вращении точки вокруг неподвижной оси…
1) …![]() ,
,![]() -
импульс тела; 2) …
-
импульс тела; 2) …![]() ,
,![]() -момент силы; 3) …
-момент силы; 3) …![]() ,
,![]() -
момент инерции материальной точки,
-
момент инерции материальной точки,![]() - угловая скорость вращения точки;
4)
- угловая скорость вращения точки;
4)![]() ,
,
![]() -
угловое ускорение; 5) …
-
угловое ускорение; 5) …![]() .
.
8. При каком виде равновесия тело обладает минимальной потенциальной энергией?
1) …безразличном; 2) …неустойчивом; 3) …безразличном и неустойчивом; 4) устойчивом; 5) …при любом виде равновесия.
9. Общее условие равновесия тел можно записать в виде следующих уравнений…
1) …![]() ;
2) …
;
2) …![]() ;
3) …
;
3) …![]() и
и![]() ;
4) …
;
4) …![]() ;
5)
;
5)![]() и
и![]() .
.
10. Условие равновесия рычага имеет вид…
1) …![]() ;
2) …
;
2) …![]() ;
3) …
;
3) …![]() ;
4) …
;
4) …![]() .
.
11. Основное уравнение динамики вращательного движения имеет вид…
1) …![]() ;
2) …
;
2) …![]() ;
3) …
;
3) …![]() ;
4) …
;
4) …![]() ;
5) …
;
5) …![]() .
.
12. При равномерном вращении тела сохраняется вектор…
1) …скорости
![]() ;
2) …нормального ускорения
;
2) …нормального ускорения![]() ;
3) …тангенциального ускорения
;
3) …тангенциального ускорения![]() ;
4) …импульса
;
4) …импульса![]() ;
5) …момента импульса
;
5) …момента импульса![]() .
.
13. Момент инерции тела Iотносительно оси, состоящего из частиц
массой![]() ,
равен…
,
равен…
1) …![]() ,
,![]() -
модуль угловой скорости; 2) …
-
модуль угловой скорости; 2) …![]() ,L- момент импульса;
3) …
,L- момент импульса;
3) …![]() ;
4) …
;
4) …![]() ;
5) …
;
5) …![]() .
.
14. Главный момент внешних сил связан с угловой скоростью основным законом динамики для вращательного движения. Укажите номер выражения для момента сил…
1) …![]() ,r – радиус, m
– масса; 2) …
,r – радиус, m
– масса; 2) …![]() ;
3) …
;
3) …![]() ;
4)
;
4)![]() ;
5) …
;
5) …![]() .
.
15. Единицей измерения модуля импульса тела является…
1) …![]() ;
2) …
;
2) …![]() ;
3) …
;
3) …![]() ;
4) …
;
4) …![]() ;
5) …
;
5) …![]() .
.
16. Закон сохранения момента импульса Lможно записать выражением…
1) …![]() ,M –момент внешних
сил; 2) …
,M –момент внешних
сил; 2) …![]() ,m – масса, v
– модуль скорости, h-
высота тела; 3) …
,m – масса, v
– модуль скорости, h-
высота тела; 3) …![]() ,
гдеI – момент
инерции;
,
гдеI – момент
инерции;
![]() -
модуль угловой скорости; 4) …
-
модуль угловой скорости; 4) …![]() ;
5) …
;
5) …![]() .
.
17. Какое из приведенных выражений позволяет записать момент импульса твердого тела?
1) …![]() ;
2) …
;
2) …![]() ;
3) …
;
3) …![]() ;
4) …
;
4) …![]() ;
5) …
;
5) …![]() .
.
18. Модуль момента силы можно вычислить по формуле…
1) …![]() ;
2) …
;
2) …![]() ;
3) …
;
3) …![]() ;
4) …
;
4) …![]() ;
5) …
;
5) …![]() .
.
19. Дано выражение:
![]() ,
где
,
где![]() -
момент импульса материальной точки,
-
момент импульса материальной точки,![]() -
время. Это выражение определяет…
-
время. Это выражение определяет…
1) …ускорение точки; 2) …кинетическую энергию точки; 3) …вектор результирующей сил, действующих на точку; 4) …вектор силы в данной точке; 5) …вектор результирующего момента сил, действующих на точку.
20. Невесомая доска покоится на двух опорах (рис. 6). Правая опора делит длину доски в отношении 1:3. На ее правый конец падает тело массой m2= 1 кг, скорость которого в момент удараv2. Если после удара это тело полностью теряет свою скорость, то тело массойm1= 1 кг начнет двигаться со скоростью...
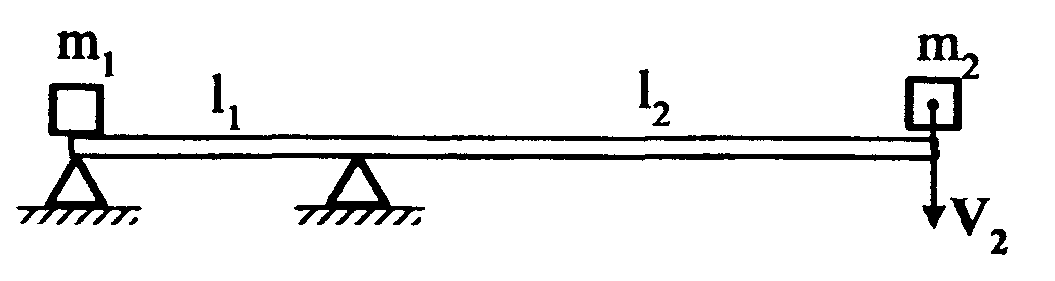 Рис.
6
Рис.
6
1) …v1
= v2; 2)
…v1 =
![]() v2;
3) …v1
=
v2;
3) …v1
=
![]() v2;
4) …v1
= 6 v2;
5) …v1 =
3 v2.
v2;
4) …v1
= 6 v2;
5) …v1 =
3 v2.
