
- •Глава 4 Закон сохранения момента импульса. Механика твердого тела
- •1 Момент силы
- •2 Момент импульса. Закон сохранения момента импульса
- •3 Плоское движение твердого тела
- •4 Вращение твердого тела вокруг неподвижной оси
- •5 Момент инерции. Теорема Штейнера
- •6 Кинетическая энергия вращающегося тела
- •7 Кинетическая энергия тела при плоском движении
ФИЗИКА
Модуль 1.4
Глава 4 Закон сохранения момента импульса. Механика твердого тела
1 Момент силы
Моментом силы относительно точки
![]() называется вектор
называется вектор![]() ,
равный векторному произведению векторов
,
равный векторному произведению векторов![]() и
и![]() :
:
![]() , (4.1)
, (4.1)
где
![]() - радиус-вектор точки приложения силы
- радиус-вектор точки приложения силы![]() ,
проведенный из точки
,
проведенный из точки![]() ,
относительно которой определяется
момент (рис. 1).
,
относительно которой определяется
момент (рис. 1).

Рис. 1
Модуль вектора
![]() равен произведению модуля силы
равен произведению модуля силы![]() на ее плечо
на ее плечо![]() :
:
![]() (4.2)
(4.2)
где
![]() - угол между
- угол между![]() и
и![]() .
.
Плечом силыназывают длину
перпендикуляра, опущенного из точки![]() на прямую, вдоль которой действует сила.
на прямую, вдоль которой действует сила.
Направлен вектор
![]() перпендикулярно к плоскости, в которой
лежат сила
перпендикулярно к плоскости, в которой
лежат сила![]() и точка
и точка![]() ,
причем так, что направление вращения,
обусловленного силой, и направление
вектора
,
причем так, что направление вращения,
обусловленного силой, и направление
вектора![]() образуют правовинтовую систему (поворот
головки винта или буравчика в направлении
силы вызвал бы перемещение винта в
направлении вектора
образуют правовинтовую систему (поворот
головки винта или буравчика в направлении
силы вызвал бы перемещение винта в
направлении вектора![]() ).
Поскольку его направление определяется
условно,
).
Поскольку его направление определяется
условно,![]() является псевдовектором.
является псевдовектором.
Если тело может вращаться вокруг точки
![]() произвольным образом, то под действием
силы тело повернется вокруг оси,
совпадающей с направлением момента
произвольным образом, то под действием
силы тело повернется вокруг оси,
совпадающей с направлением момента![]() .
Момент силы
.
Момент силы![]() называют такжевращающим моментом.
называют такжевращающим моментом.
Проекция вектора
![]() на произвольную ось
на произвольную ось![]() ,
проходящую через точку
,
проходящую через точку![]() ,
называетсямоментом силы относительно
этой оси:
,
называетсямоментом силы относительно
этой оси:
![]() . (4.3)
. (4.3)
Разложим силу
![]() на три составляющие, как показано на
рис. 2, а именно
на три составляющие, как показано на
рис. 2, а именно
![]()
где
![]() - параллельная оси
- параллельная оси![]() ,
,![]() - перпендикулярная оси
- перпендикулярная оси![]() ,
,![]() - направленная по касательной к окружности
радиуса
- направленная по касательной к окружности
радиуса![]() .
.

Рис. 2
Представим момент силы
![]() относительно точки
относительно точки![]() в виде
в виде
![]() .
.
Моменты
![]() и
и![]() перпендикулярны к оси
перпендикулярны к оси![]() ,
поэтому их проекции на эту ось
,
поэтому их проекции на эту ось![]() равны нулю. Следовательно ,
равны нулю. Следовательно ,
![]() (4.4)
(4.4)
Из трех составляющих силы
![]() вращение вокруг оси
вращение вокруг оси![]() может вызвать только сила
может вызвать только сила![]() ,
причем она тем лучше осуществит этот
поворот, чем больше ее плечо
,
причем она тем лучше осуществит этот
поворот, чем больше ее плечо![]() относительно точки
относительно точки![]() .
.
Две равные по модулю противоположно
направленные силы, не действующие вдоль
одной прямой, называются парой сил(рис. 3). Расстояние![]() между прямыми, вдоль которых действуют
силы, называется плечом пары.
между прямыми, вдоль которых действуют
силы, называется плечом пары.

Рис. 3
Суммарный момент сил относительно точки
![]() равен
равен
![]() .
.
Учтя, что
![]() ,
можно написать
,
можно написать
![]() , (4.5)
, (4.5)
где
![]() (рис. 3). Полученное выражение не зависит
от положения точки
(рис. 3). Полученное выражение не зависит
от положения точки![]() .
Следовательно, момент пары сил относительно
любой точки будет одним и тем же. Вектор
.
Следовательно, момент пары сил относительно
любой точки будет одним и тем же. Вектор![]() перпендикулярен к плоскости, в которой
лежат силы, а его модуль равен произведению
любой из сил на плечо:
перпендикулярен к плоскости, в которой
лежат силы, а его модуль равен произведению
любой из сил на плечо:
![]() . (4.6)
. (4.6)
Силы гравитационного и кулоновского
взаимодействия между двумя частицами
образуют пару с плечом
![]() ,
равным нулю. Поэтому их суммарный момент
относительно любой точки равен нулю.
,
равным нулю. Поэтому их суммарный момент
относительно любой точки равен нулю.
Отсюда следует, что сумма моментов всех внутренних сил для любой системы частиц всегда равна нулю:
![]() (4.7)
(4.7)
2 Момент импульса. Закон сохранения момента импульса
Моментом импульса материальной точки
(частицы) относительно точки
![]() называется векторная величина
называется векторная величина
![]() , (4.8)
, (4.8)
где
![]() - радиус- вектор, определяющий положение
частицы относительно точки
- радиус- вектор, определяющий положение
частицы относительно точки![]() ,
,![]() - импульс частицы (рис. 4).
- импульс частицы (рис. 4).
Модуль момента импульса равен
![]() ,
(4.9)
,
(4.9)
где
![]() - плечо импульса
- плечо импульса![]() .
.

Рис. 4
Частица обладает моментом импульса
![]() ,
независимо от формы траектории, по
которой она движется. Рассмотрим два
частных случая.
,
независимо от формы траектории, по
которой она движется. Рассмотрим два
частных случая.
1. Частица движется по прямолинейной траектории (рис. 5).
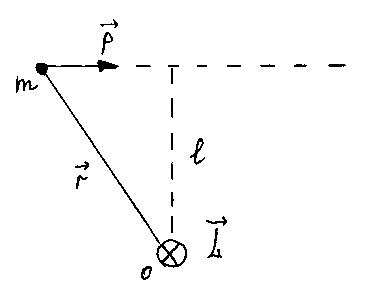
![]()
Рис. 5
2. Частица движется по окружности радиуса
![]() (рис. 6).
(рис. 6).

![]()
Рис. 6
Проекция вектора
![]() на произвольную ось
на произвольную ось![]() ,
проходящую через точку
,
проходящую через точку![]() ,
называетсямоментом импульса частицы
относительно этой оси:
,
называетсямоментом импульса частицы
относительно этой оси:
![]() . (4.10)
. (4.10)
Выясним, от чего зависит изменение момента импульса. Для этого продифференцируем выражение (4.8) по времени:
![]()
Учитывая, что
![]() ,
,![]() ,
а
,
а![]() ,
,![]() ,
мы приходим куравнению моментов:
,
мы приходим куравнению моментов:
![]() , (4.11)
, (4.11)
согласно которому скорость изменения момента импульса со временем равна суммарному моменту сил, действующих на частицу.
Записав уравнение (4.11) в проекции на ось
![]() ,
получим
,
получим
![]() . (4.12)
. (4.12)
Таким образом, производная по времени от момента импульса относительно оси равна моменту сил, действующих на частицу, относительно той же оси.
Рассмотрим систему частиц, на которые
действуют как внутренние, так и внешние
силы. Момент импульса
![]() системы относительно точки
системы относительно точки![]() равен:
равен:
![]() . (4.13)
. (4.13)
Дифференцирование по времени дает, что
![]()
Учитывая (4.11), получим:
![]() .
.
Согласно (4.7)
![]() ,
поэтому получаем окончательно, что
,
поэтому получаем окончательно, что
![]() . (4.14)
. (4.14)
или в проекциях на произвольную ось
![]()
![]()
![]() (4.15)
(4.15)
Если система замкнута (т.е. внешних сил
нет), правая часть равенства (4.15) равна
нулю и, следовательно, вектор
![]() не изменяется со временем. Отсюда
вытекаетзакон сохранения момента
импульса: момент импульса замкнутой
системы материальных точек остается
постоянным. Согласно (4.15) в незамкнутой
системе сохраняется момент импульса
системы относительно оси
не изменяется со временем. Отсюда
вытекаетзакон сохранения момента
импульса: момент импульса замкнутой
системы материальных точек остается
постоянным. Согласно (4.15) в незамкнутой
системе сохраняется момент импульса
системы относительно оси![]() ,
т.е.
,
т.е.![]() ,
при условии, если сумма моментов внешних
сил относительно этой оси равна нулю:
,
при условии, если сумма моментов внешних
сил относительно этой оси равна нулю:![]() .
.
В основе закона сохранения момента импульса лежит изотропия пространства, т.е. одинаковость свойств пространства по всем направлениям. Поворот замкнутой системы частиц без изменения их взаимного положения и относительных скоростей не изменяет механических свойств системы. Движение частиц друг относительно друга после поворота будет таким же, как до поворота.
