3 Сложение взаимно перпендикулярных колебаний
Предположим, что
имеются две взаимно перпендикулярные
векторные величины
и
,
изменяющиеся
со временем с одинаковой частотой
по гармоническому закону
,
(6.6)
Здесь
и
— орты
координатных осей
и
,
и
— амплитуды
колебаний. Величинами
и
могут быть, например, смещения материальной
точки (частицы) из положения равновесия
или напряженности двух взаимно
перпендикулярных электрических полей
(
и
)
и т. п. В случае колеблющейся частицы
величины
,
(6.7)
определяют
координаты частицы на плоскости
.
В случае
электрических полей величины (6.7)
определяют координаты конца результирующего
вектора напряженности поля
.
Частица или конец
вектора
будут двигаться по некоторой траектории,
вид которой зависит от разности фаз
обоих колебаний. Выражения (6.7) представляют
собой заданное в параметрической форме
уравнение этой траектории. Чтобы
получить уравнение траектории в обычном
виде, нужно исключить из уравнений
(6.7) параметр
.
Из первого уравнения следует, что
(6.8)
Соответственно
. (6.9)
Развернем косинус
во втором из уравнений (6.7) по формуле
для косинуса суммы (
),
подставляя при этом вместо
и
их значения (6.8) и (6.9). В результате
получим
.
Это уравнение посредством очевидных преобразований можно привести к виду
(6.10)
Мы получили
уравнение эллипса, оси которого повернуты
относительно координатных осей
и
.
Ориентация эллипса и его полуоси зависят
довольно сложным образом от амплитуд
и
и разности фаз
.
.
Определим форму траектории для нескольких частных случаев.
1. Разность фаз
равна нулю.
В этом случае уравнение (6.10) упрощается
следующим образом:
.
Отсюда получается уравнение прямой:
(6.11)
Результирующее
движение является
гармоническим колебанием вдоль этой
прямой с частотой
и амплитудой, равной
(рис.
5а).
2. Разность фаз
равна ±
.
Уравнение (6.10) имеет вид
Следовательно, результирующее движение представляет собой гармоническое колебание вдоль прямой
(6.12)
(рис. 5.6).
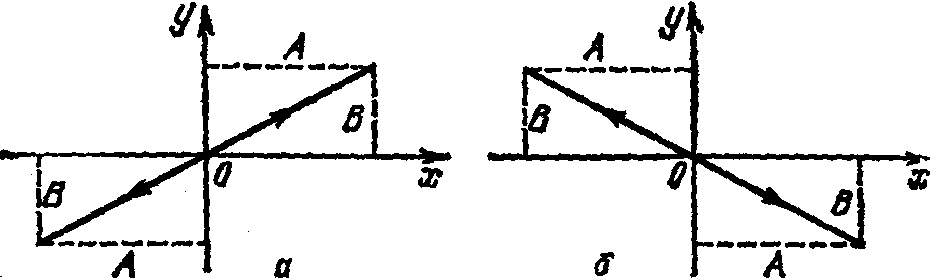
Рис. 5
3.
При
уравнение (6.10) переходит в уравнение
эллипса, приведенного к координатным
осям
(6.13)
Полуоси эллипса
равны соответствующим амплитудам
колебаний. При равенстве амплитуд
и
эллипс вырождается в окружность.
Случаи
и
отличаются направлением движения по
эллипсу или окружности. Если
,
уравнения (6.7) можно написать следующим
образом:
,
. (6.14)
В момент
тело находится в точке 1 (рис. 6). В
последующие моменты времени координата
уменьшается,
а координата
становится
отрицательной. Следовательно, движение
совершается по часовой стрелке.
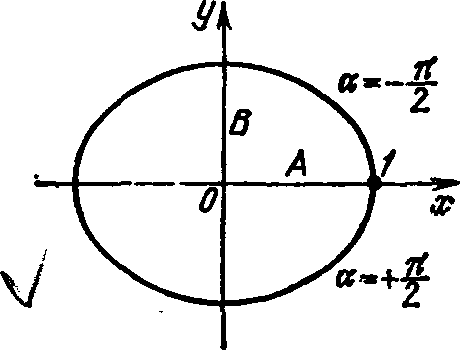
Рис. 6
При
уравнения (6.7) имеют вид
,
.
Отсюда заключаем, что движение происходит против часовой стрелки.
Из сказанного
вытекает, что равномерное движение по
окружности радиуса
с угловой скоростью
может быть представлено как сумма двух
взаимно перпендикулярных колебаний:
,
. (6.15)
(знак плюс в
выражении для
соответствует движению против часовой
стрелки, знак минус — движению по
часовой стрелке).
Если частоты взаимно перпендикулярных колебаний не одинаковы, то траектории результирующего движения имеют вид довольно сложных кривых, называемых фигурами Лиссажу. На рис. 7 и 8 приведены примеры таких фигур.
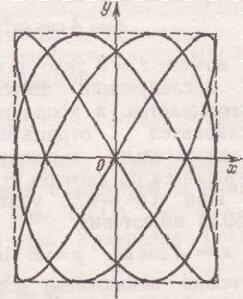
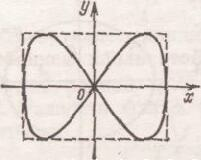
Рис. 7 Фигура Лиссажу для отношения Рис. 8 Фигура Лиссажу для отношения
частот 3:4
и разности фаз
частот1:2 и разности фаз
Задачи
Задача 1 Складываются два колебания одинакового направления, выраженные уравнениями:
,
,
где
= 3 см,
= 2 см,
с,
с,
= 2 с.
Построить векторную диаграмму сложения этих двух колебаний и написать уравнение результирующего колебания.
Решение
Обычно векторную
диаграмму строят для момента времени
= 0. Преобразовав оба уравнения к
каноническому виду
,
получим
,
.
Отсюда видно, что оба гармонических колебания имеют одинаковую циклическую частоту
.
Начальные фазы
первого и
второго колебаний соответственно
равны:
,
.
Подставив числовые значения величин получим
,
На рис. изобразим
векторы
и
.
Для этого отложим отрезки длиной
= 3 см и
=
2 см под углом
= 300
и
= 600
к оси
.
Результирующее
колебание будет происходить с той же
частотой
и амплитудой
,
равной
.
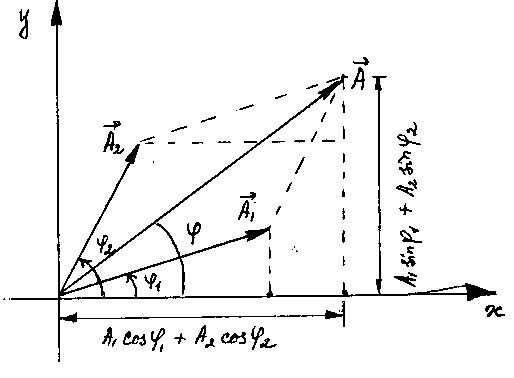
Согласно теореме косинусов
Начальная фаза
определяется так:
.
Подставим числовые значения и получим
(см)
или
= 0,735 рад.
Результирующее колебание имеет вид:
или
см.
Задача 2 Материальная точка участвует в двух взаимно перпендикулярных гармонических колебаниях, уравнения которых:
, (1)
, (2)
где
= 1 см,
рад/с,
= 2 см,
рад/с.
Определить и построить траекторию точки.
Решение
Чтобы определить
траекторию точки, исключим время из
уравнений (1) и (2). Заметив, что
,
применим формулу косинуса половинного
угла:
.
В результате
,
.
Отсюда найдем
,
или
.
Это уравнение
представляет собой уравнение параболы,
ось которой лежит на оси
.
Как показывают уравнения (1) и (2), амплитуда
колебаний точки по оси
равна 1, а по оси
- 2. Следовательно, абсциссы всех точек
траектории заключены в пределах от -1
до +1, а ординаты – от -2 до +2. Таким
образом, траектория
представляет собой часть параболы
(рис.)
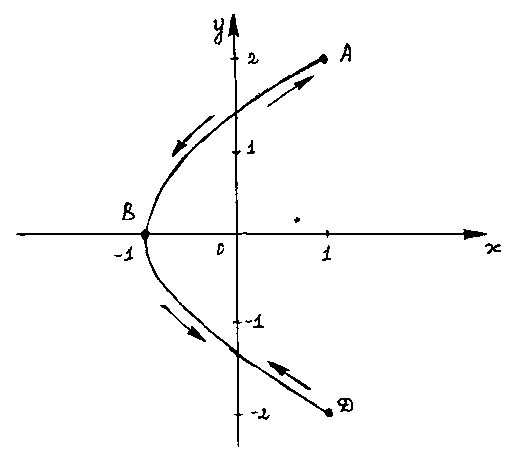
В начальный момент
времени (
)
имеем
= 1,
= 2. Точка находится в положении
.
При
= 1 с, получим
= -1,
= 0, т.е. точка находится в вершине параболы
(
).
При
= 2 с
= 1,
= -2 в положении
.
После этого она будет двигаться в
обратном направлении.
Задача 3
Написать уравнение результирующего
колебания, получающегося в результате
сложения двух взаимно перпендикулярных
колебаний с одинаковой частотой
Гц и одинаковой начальной фазой
.
Амплитуды колебаний равны
=
0,1 м,
= 0,05 м.
Решение
Имеем
,
,
причем
,
.
Поделив уравнения, получим
- уравнение прямой
линии.
Таким образом, результирующее колебание будет происходить по прямой линии. Угол наклон найдем из уравнения
,
т.е.
.
Частота
результирующего колебания
,
амплитуда
см. Следовательно, уравнение результирующего
колебания имеет вид
см.
Тесты
1. Складываются
два гармонических колебания одного
направления с одинаковыми периодами
и равными амплитудами
.
При разности фаз
амплитуда результирующего колебания
равна…
1. – 0; 2. –
;
3. –
;
4. –
;
5. –
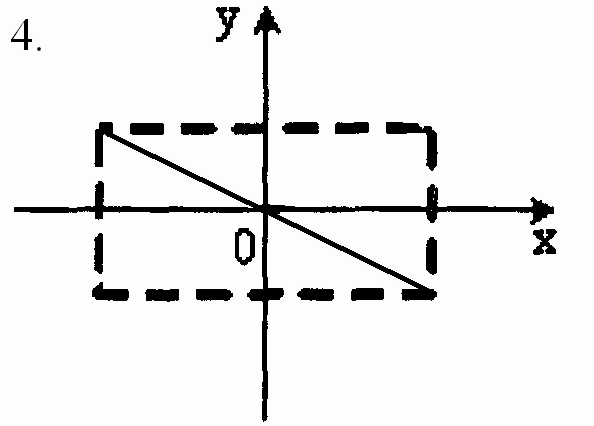
2. Точка M одновременно колеблется по гармоническому закону вдоль осей координат OX и OY с различными амплитудами, но одинаковыми частотами. При разности фаз π/2 траектория точки M имеет вид:
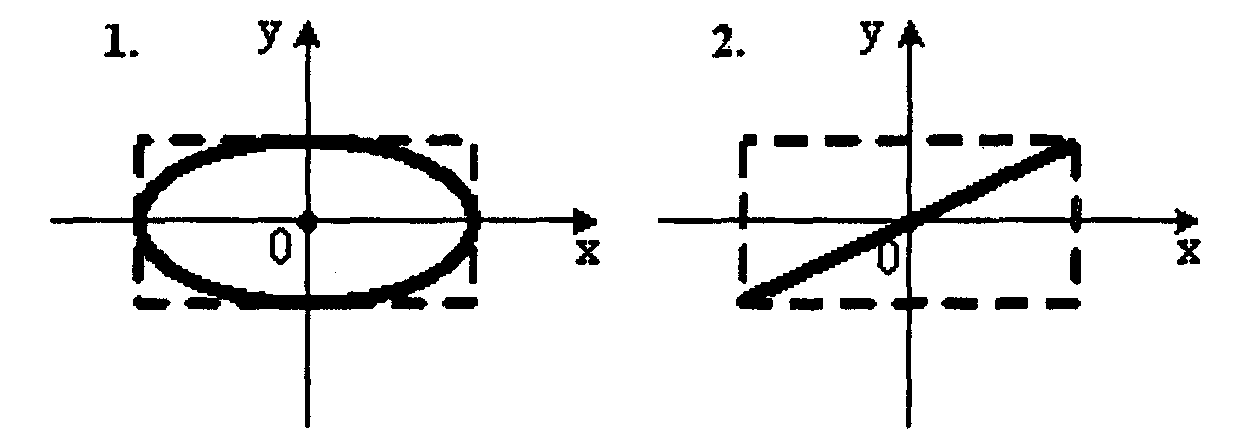
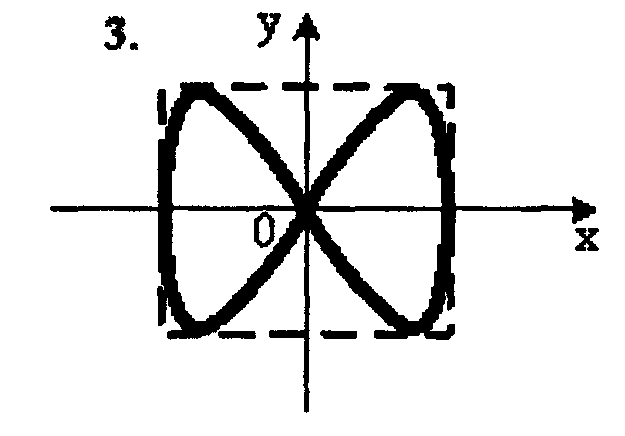
1.– 2; 2. – 3; 3. – 4; 4. – 1.
3. Точка M одновременно колеблется по гармоническому закону вдоль осей координат OX и OY с различными амплитудами, но одинаковыми частотами. При разности фаз 0 траектория точки M имеет вид:
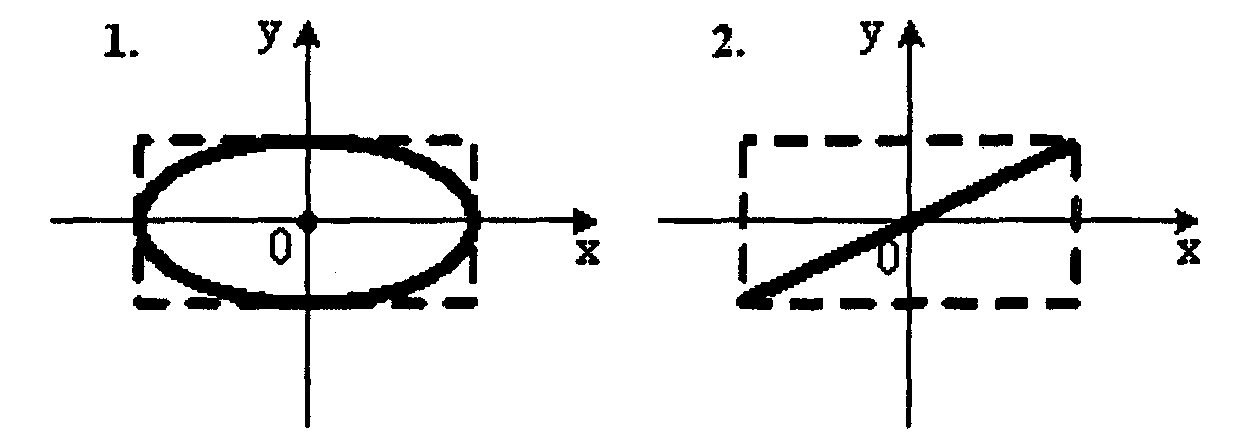
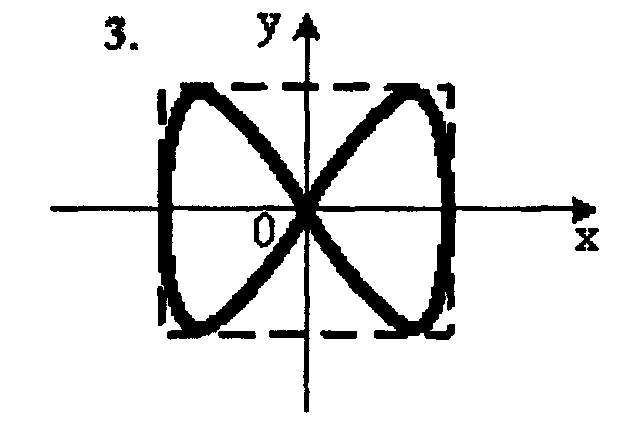
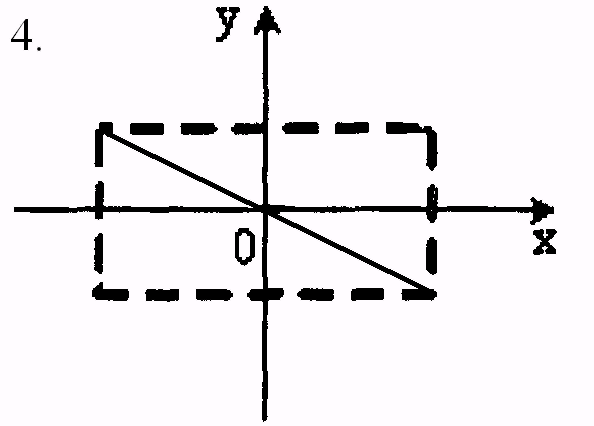
1.– 2; 2. – 3; 3. – 4; 4. – 1.
4. Точка M
одновременно колеблется по гармоническому
закону вдоль осей координат OX
и OY
с различными амплитудами, но одинаковыми
частотами. При разности фаз
траектория точки M
имеет вид:
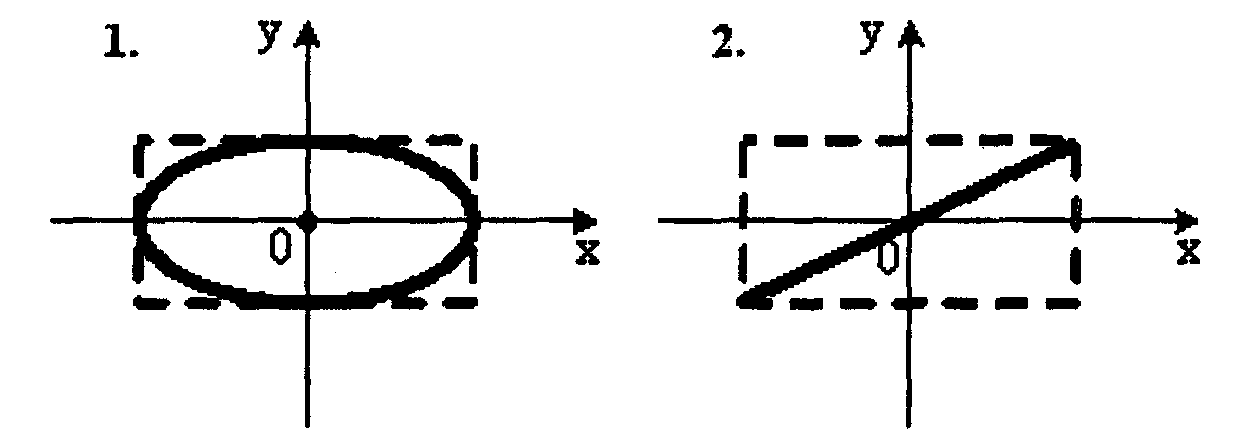
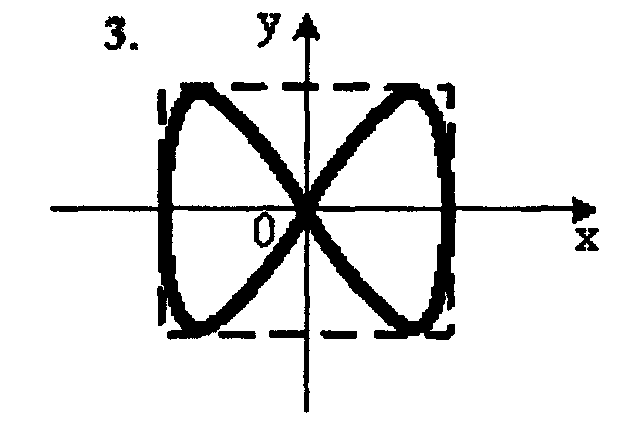
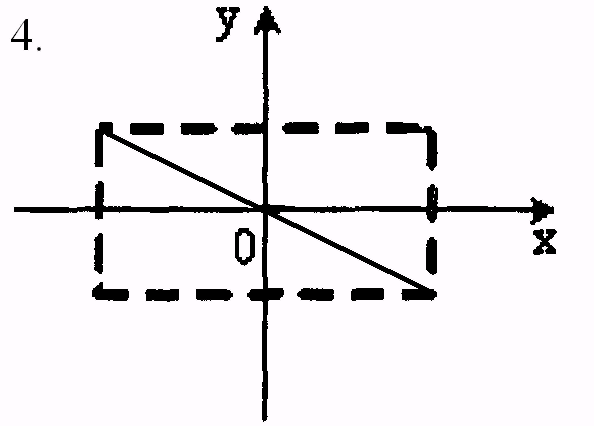
1.– 2; 2. – 3; 3. – 4; 4. – 1.
5. Точка M
одновременно колеблется по гармоническому
закону вдоль осей координат OX
и OY
с различными амплитудами, но с кратными
частотами (
).
При разности фаз π/2 траектория точки
M
имеет вид:
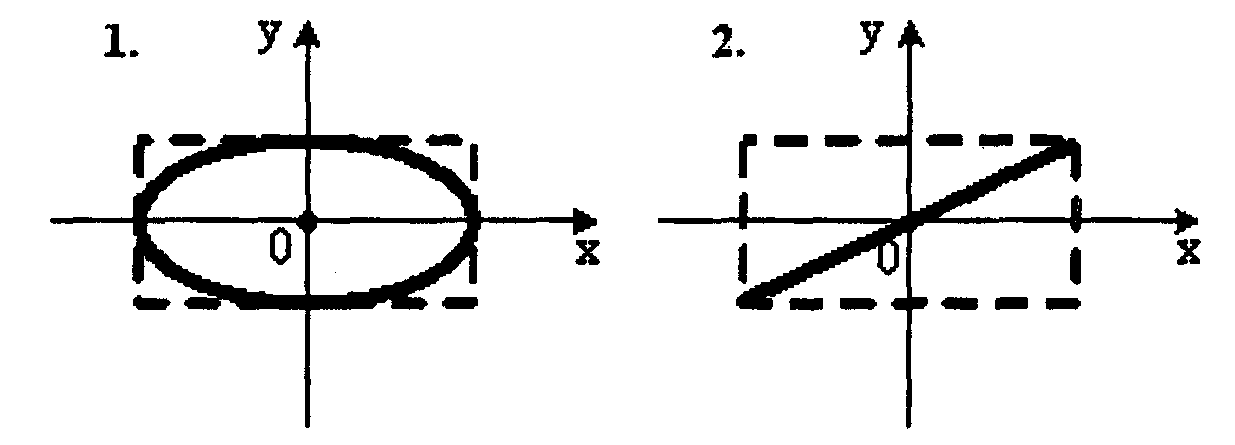
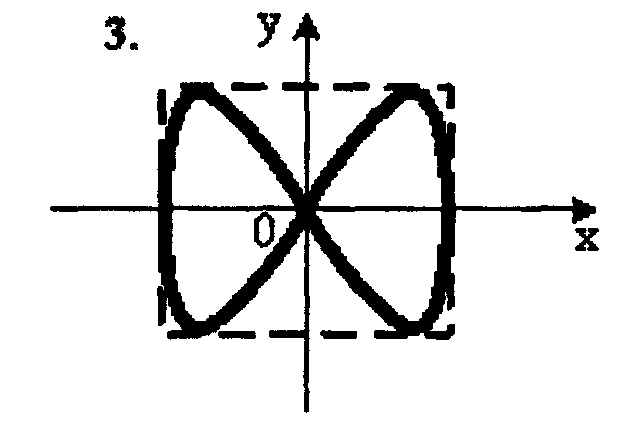
1.– 2; 2. – 3; 3. – 4; 4. – 1.
6. Складываются два гармонических колебания одного направления с одинаковыми периодами. Результирующее колебание имеет максимальную амплитуду при разности фаз, равной…
1. – π/2; 2. – π; 3. – π/4; 4. – 0.
7. Какова разность фаз двух одинаковых колебаний, если при их сложении получаются колебания с той же амплитудой?
1. – π; 2. – π/2; 3. – π/6; 4. – 2π/3; 5. – π/3.
8. Складываются
два гармонических колебания одного
направления с одинаковыми частотами
и равными амплитудами
.
При разности фаз
амплитуда результирующего колебания
равна…
1. – 0; 2. –
;
3. –
;
4. –
.
9. Какова разность
фаз двух одинаковых колебаний, если
при их сложении получаются колебания
с амплитудой в
раза большей?
1. – π; 2. – π/2; 3. – π/6; 4. – 2π/3; 5. – π/3.
10. Складывают колебания одинаковой частоты и направления с разными фазами. При какой разности фаз результирующая амплитуда колебания будет минимальной?
1. – π/4; 2. – π/2; 3. – π/3; 4. – π; 5. – 2π.
11. При сложении взаимно перпендикулярных колебаний одной частоты с разностью фаз равной нулю получаются колебания вида:
1. – эллипс; 2. – прямая линия; 3. – окружность; 4. – парабола; 5. – гипербола.
12. Явление биений возникает:
1. – при большом затухании колебаний; 2. – при сложении одинаково направленных колебаний с кратными частотами; 3. – при сложении одинаково направленных колебаний с близкими частотами; 4. – при резонансе; 5. – при сложении взаимно перпендикулярных колебаний.