3 Барометрическая формула

Известно, что атмосферное давление убывает с высотой. Найдем функцию , описывающую зависимость давления от высоты.

Выделим мысленно в атмосфере вертикальный столб с площадью поперечного сечения , равной единице. Атмосферное давление на высотеобусловлено весом столба воздуха, который простирается от сечения, расположенного на данной высоте, до внешней границы атмосферы. Поэтому давление с высотойубывает. Напомним, чтоозначает приращение давления, которое отличается от убыли знаком. Убыль давленияпри переходе от высотык высотеравна весу воздуха, заключенного в элементе столба высоты:

(3.35)

где - плотность воздуха на высоте.

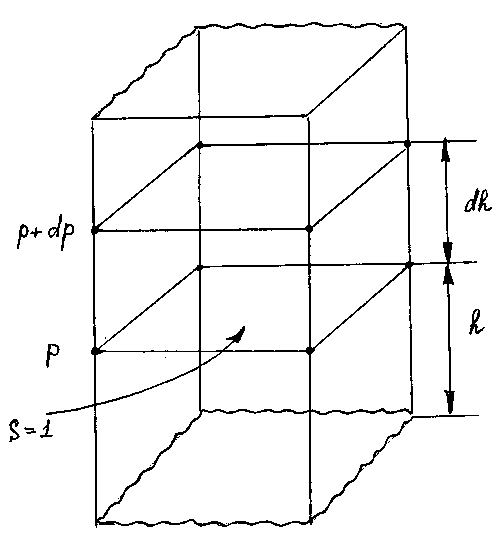
Рис. 8

При условиях, близких к нормальным (т.е. при = 1 атм и= 0⁰ С) воздух довольно хорошо подчиняется уравнению состояния идеального газа.

Из уравнения Клапейрона - Менделеева следует, что плотность идеального газа равна

. (3.36)

Подставим это выражение в формулу (3.35) и получим

. (3.37)

Здесь - молярная масса воздуха.

Разделив переменные, придем к дифференциальному уравнению

(3.38)

Для изотермической атмосферы, т.е. для случая, когда температура с высотой не изменяется, интегрирование (3.38) приводит к соотношению:

или потенцируя, получим

(3.39)

Здесь - атмосферное давление на высоте, принятой за начало отсчета. Таким образом, зависимость давления от высотыописывается формулой (3.39), которая называетсябарометрической формулой.

4 Распределение Больцмана

В формуле (3.39) представим

,

где - масса молекулы,- постоянная Больцмана,, где- концентрация молекул газа. В результате придет к соотношению

.

Таким образом,

(3.40)

Здесь - плотность молекул или их концентрация при,- на высоте.

Выражение представляет собой потенциальную энергию молекулы.

Поэтому формулу (3.40) можно написать следующим образом:

(3.41)

Л. Больцман доказал, что формула (3.41) справедлива в случае потенциального силового поля любой природы для совокупности любых одинаковых частиц, находящихся в состоянии теплового движения. В связи с этим функцию (3.41) называют распределением Больцмана. Распределение (3.40) – частный случай более общего распределения (3.41).

5 Распределение Максвелла – Больцмана

Между распределениями Больцмана и Максвелла имеется большое сходство.

Возьмем элементарный объем , расположенный в точке с координатами. Согласно формуле (3.41) в пределах этого объема находится число молекул

(3.42)

Эта формула обнаруживает еще большее сходство с распределением Максвелла, которое можно представить в виде:

, (3.43)

где (см. фор. 3.17).

Заметим, что кинетическая энергия равна

.

Распределение (3.42) и (3.43) можно объединить в один закон Максвелла- Больцмана, согласно которому число молекул, компоненты скоростей которых лежат в пределах от до,,, а координаты – в пределах отдо,,, равно

(3.44)

Здесь нормированный множитель , потенциальная энергия, кинетическая энергия,, элемент объема.

Задачи

Задача 1 Функция распределения вероятностей Распределение вероятностей некоторой величины описывается формулой~в интервале. Вне этого интервала. Найти: а) наиболее вероятное и среднее значения величины; б) вероятность нахожденияв интервале.

Решение

а) Наиболее вероятное значение соответствует максимуму функции. Из рис. сразу видно, что. Это случай, не требующий выполнения условия

.

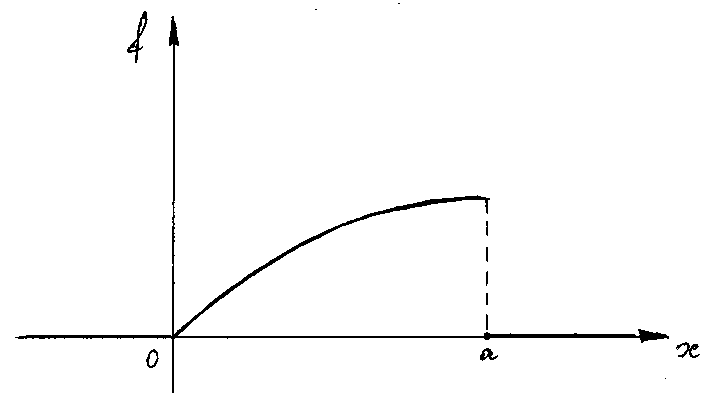
Рис.

Среднее значение по определению есть

,

где - нормировочный множитель. Его находим из условия

,

откуда .

В результате подстановки значения и интегрирования получим

.

б) По определению искомая вероятность

.

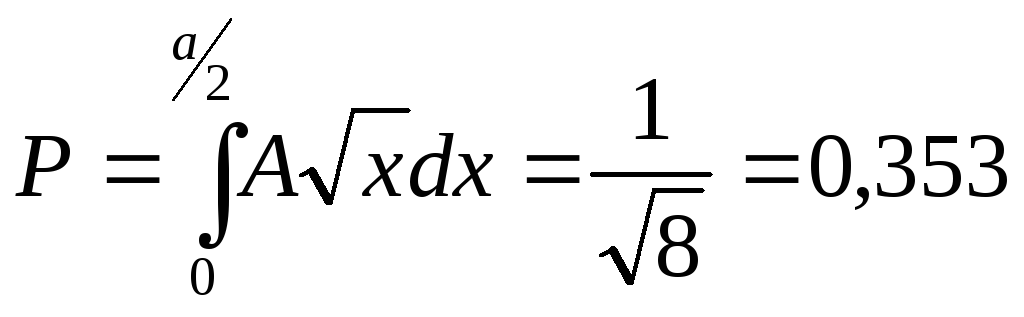Задача 2 Распределение Максвелла Найти с помощью распределения Максвелла среднее значение модуля проекции скорости , если температура газаи масса каждой молекулы.

Решение

По определению искомая величина

(1) Поскольку интегральная функция всюду положительна и симметрична относительно начала координат (), то интеграл (1) можно записать так:

(2)

После подстановки функции и некоторых преобразований получим

, где . Учитывая, что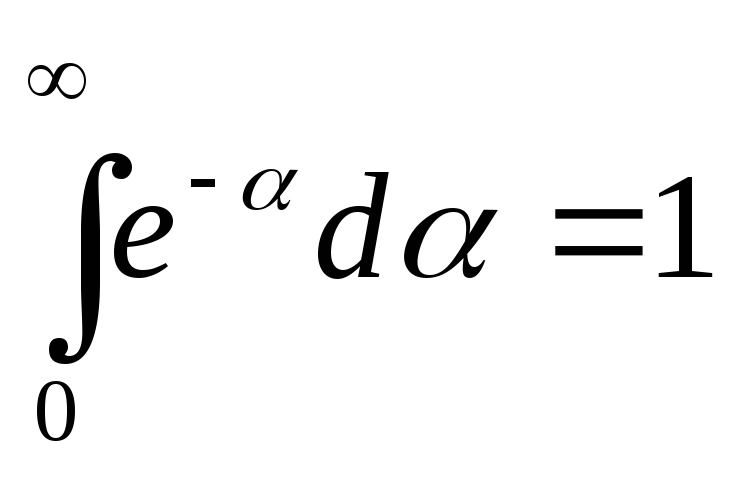, получим

.

Задача 3 Барометрическая формула На какой высоте давление воздуха составляет 75% от давления на уровне моря? Температуру считать постоянной, равной 0⁰ С. Молярная масса воздуха = 29·10^-3 кг/моль.

Решение

Убывание давления газа с высотой определяется барометрической формулой (3.39)

или

Следовательно

, м.

Задача 4 Распределение Больцмана При наблюдении в микроскоп взвешенных частиц гуммигута (сгущенного млечного сока, получаемого из надрезов в коре некоторых видов деревьев, растущих в Южной Азии) французский физик Перрен определил постоянную Больцмана и постоянную Авогадро. Он обнаружил, что среднее число их в тонких слоях 1 и 2, расстояние между которыми по высоте равно, отличается друг от друга враз. Температура среды, диаметр частици их плотностьбольше плотности окружающей жидкости. Найти по этим данным постоянную Больцманаи постоянную Авогадро.

Решение

Согласно распределению Больцмана отношение частиц в слоях 1 и 2 определяется как

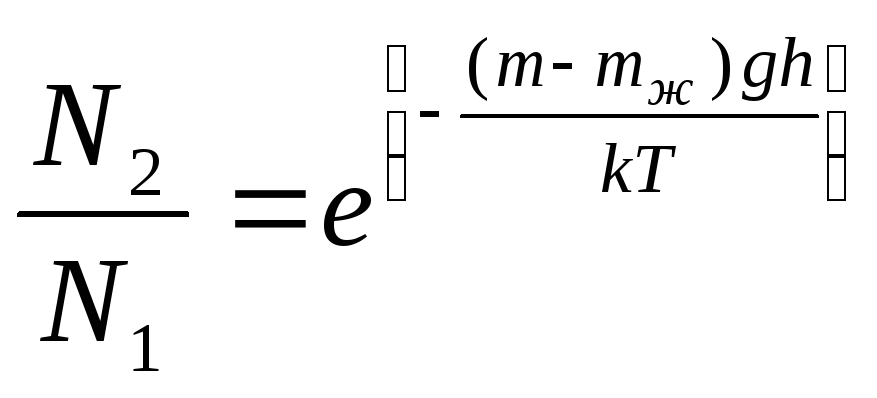, (1)

где учтено, что на частицу массу действует сила тяжестии сила Архимеда). Преобразуем разность масс в круглых скобках выражения (1)

. (2)

После подстановки (2) в (1) соотношение (1) представим в виде

, (3)

отсюда, имея в виду, что , следует

.

, где = 8,31 Дж/моль·К – универсальная газовая постоянная.

Задача 5 Распределение Максвелла в приведенном виде Какая часть молекул газа имеет скорости, превышающие наиболее вероятную скорость?

Решение

Формула (3.30) позволяет определить в любом интервале скоростей

,

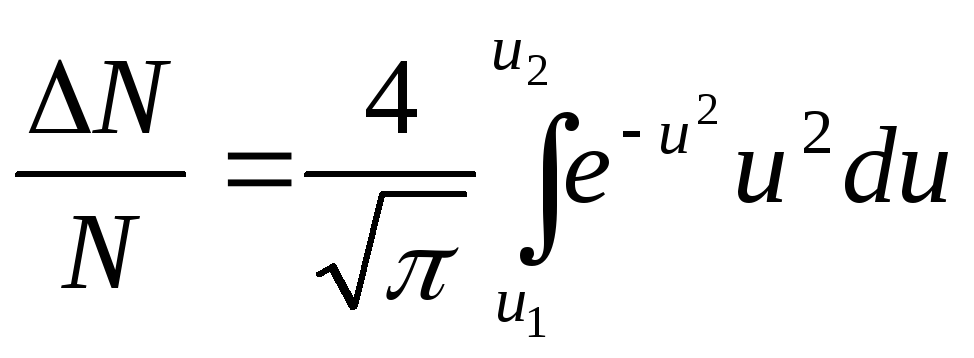где .

В нашем случае ,.

Следовательно, .

Пусть - число молекул, скорость которых меньше наиболее вероятной, т.е. лежат в интервале от 0 доилиизменяется в пределах от 0 до 1, тогда

Задача 6 Какая часть молекул водорода, находящегося при температуре , обладает скоростями, отличающимися от наиболее вероятной скорости не более, чем на 5,0 м/с? Задачу решить для двух значений: 1) 400 К; 2) 900 К.

Решение

Убедимся, что выполняется условие или. Наиболее вероятная скорость

,

м/с

м/с.

Отсюда

;

;

Так как в нашем случае , то.

Поэтому в расчетах можно воспользоваться формулой (3.34):

.

Подстановка числовых значений дает

Тесты

1. На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где – доля молекул, скорости которых заключены в интервале скоростей отv до v+dv в расчете на единицу этого интервала. Выберите верные утверждения.

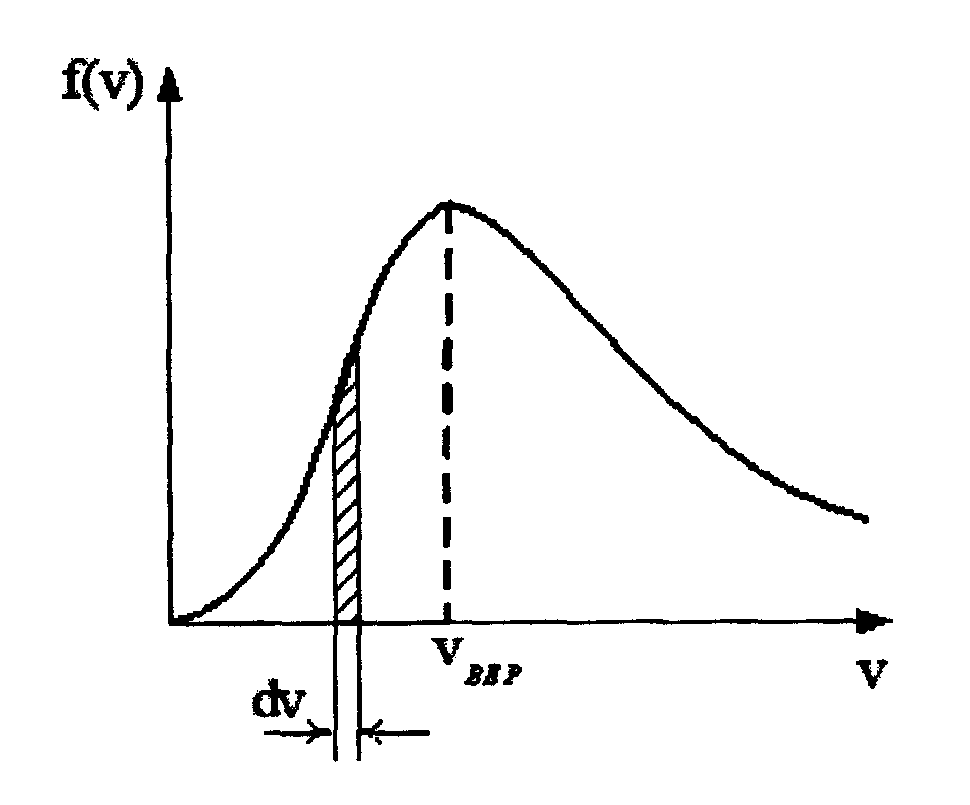
Рис.1

А. Площадь заштрихованной плоскости равна доле молекул со скоростями в интервале от v до v+dv.

В. При понижении температуры максимум кривой смещается влево.

С. При понижении температуры площадь кривой уменьшается.

1. – А, В и С; 2. – А и В; 3. – А и С; 4. – В и С.

2. На рисунке 1 представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где – доля молекул, скорости которых заключены в интервале скоростей отv до v+dv в расчете на единицу этого интервала. Выберите верные утверждения.

А. Положение максимума кривой зависит как от температуры, так и от природы газа.

В. При понижении температуры максимум кривой смещается влево.

С. При понижении температуры площадь под кривой уменьшается.

1. – А и В; 2. – В и С; 3. – А и С; 4. – А, В и С.

3. На рисунке 1 представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где – доля молекул, скорости которых заключены в интервале скоростей отv до v+dv в расчете на единицу этого интервала. Выберите верные утверждения.

А. С ростом температуры максимум кривой смещается вправо.

В. С ростом температуры площадь кривой не изменяется.

С. Вид функции распределения не зависит от природы газа (от массы молекул).

1. – А, В и С; 2. – только С; 3. – В и С; 4. – А и В; 5. – только В.

4. Атмосферное давление с ростом высоты над уровнем земли…

1. – растет линейно; 2. – уменьшается линейно; 3. – уменьшается экспоненциально; 4. – растет экспоненциально; 5.– уменьшается обратно пропорционально квадрату высоты.

5. Каким газам: водороду (Н₂), гелию (Не) или кислороду (О₂) соответствуют зависимости 1, 2, 3? Р – давление газов на высоте h, температуры газов одинаковы.

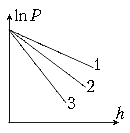
1. – 1 – гелий, 2 – кислород, 3 – водород; 2. – 1 – кислород, 2 – водород, 3 – гелий; 3. – 1 – водород, 2 – гелий, 3 – кислород; 4. – 1 – гелий, 2 – водород, 3 – кислород; 5. – 1 – водород, 2 – кислород, 3 – гелий.

6. Какой из перечисленных скоростей не существует?

1. – наиболее вероятной ; 2. – среднеарифметической; 3. – среднеквадратичной; 4. – полусредней; 5. – средней по абсолютному значению.

7. В трех одинаковых сосудах при равных условиях находятся одинаковое количество водорода, гелия и азота.

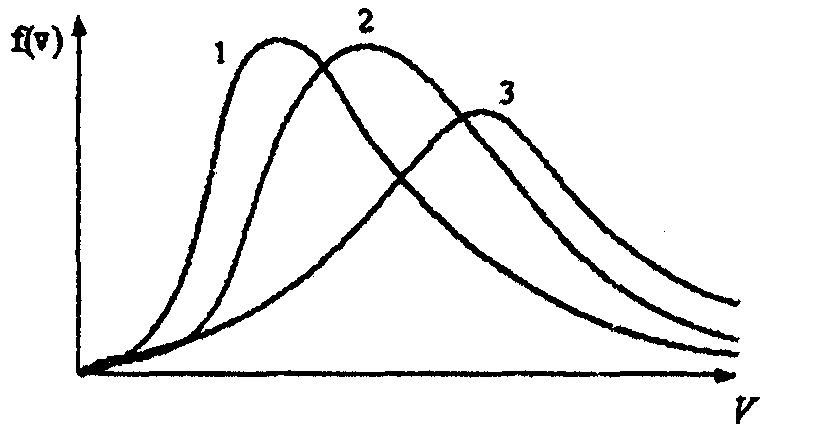
Распределение скоростей молекул гелия будет описывать кривая…

1. – 2; 2. – 1; 3. – 3.

8. Какая формула представляет функцию распределения Максвелла?

1. – ; 2. –; 3. –; 4. –; 5. –.

9. Барометрическую формулу можно представить в виде:

1. – ,– молярная масса,– концентрация молекул на высоте,– универсальная газовая постоянная,– абсолютная температура; 2. –,– постоянная Больцмана; 3. –,– диаметр молекул,– концентрация,– средняя скорость,– число столкновений; 4. –,- масса молекулы; 5. –.

10. Функция распределения Больцмана определяет распределение молекул идеального газа по…

1. – размерам; 2. – скоростям; 3. – молекулярным массам; 4. – энергии; 5. – импульсам.

11. Если два идеальных газа при одинаковой температуре имеют одну и ту же функцию распределения Максвелла, то у этих газов…

1. – одинаковое количество молекул; 2. – одинаковый объем; 3. – одинаковое давление; 4. – одинаковая молярная масса; 5. – одинаковое число молей.

20