Цикл Карно

Созданный французским инженером Сади Карно в 1824 г первый тепловой двигатель состоял из нагревателя с температурой , холодильника си рабочего тела, т.е. устройства, способного получать тепло и совершать работу (рис. 5). Под рабочим телом пока будем понимать идеальный газ в цилиндре с поршнем.

Рис. 5

Карно рассмотрел цикл из двух изотерм и двух адиабат (изэнтроп) (рис. 6).

При изотермическом расширении газ находится в контакте с нагревателем (). Пусть при этом газ получает тепло. На изотерме 3-4 газ отдает теплохолодильнику (). В соответствии с (4.21) КПД двигателя

(4.22)

Данный цикл является обратимым (если его проводить бесконечно медленно). Он может быть проведен в обратном направлении, и при этом газ совершает отрицательную работу, нагреватель получает обратно тепло , холодильник отдает тепло, которое он получил в прямом цикле. Именно так в принципе работает любой бытовой холодильник.

Предельно просто выглядит цикл Карно на диаграмме (температура – энтропия). На этой диаграмме цикл Карно имеет вид прямоугольника (рис. 7).

Рис. 6

Рис. 7

Изотермы изображаются прямыми и, адиабаты (изэнтропы) – прямымии.

Согласно (4.3) , тогда полученное теплои равно площади под отрезком. Отданное холодильнику теплоилии равно площади под отрезком. При этом площадь прямоугольника равна.

Подставив ив формулу (4.21), получим равенство

,

из которого следует, что КПД цикла Карно

. (4.23)

При выводе этой формулы не делалось никаких предположений о свойствах рабочего вещества и устройстве теплового двигателя. Отсюда следует знаменитая теорема Карно: КПД обратимых двигателей, работающих по циклу Карно, зависит только от температурынагревателя и температурыхолодильника, но не зависит ни от устройства двигателя, ни от рода рабочего вещества.

Можно показать, что КПД любого необратимого теплового двигателя, работающего с теми же нагревателем и холодильником, всегда меньше, чем у двигателя, работающего по обратимому циклу Карно:

, (4.24)

где определяется формулой (4.23).

Вывод: КПД, определяемый формулой , является предельным. Никакими способами нельзя получить КПД, превышающий это значение. КПД реальных двигателей бывает намного меньше этого значения.

Задачи

Энтропия

Задача 1В ходе обратимого изотермического процесса, протекающего при= 350 К, тело совершило работу= 8 Дж, а внутренняя энергия тела получила приращение= 7,5 Дж. Найти приращение энтропии тела.

Решение

Из первого начало термодинамики следует, что в ходе процесса тело получило количество теплоты . С учетом того, что,

;

.

Задача 2Найти приращение энтропииодного моля одноатомного идеального газа при обратимом изобарическом нагревании его от 0 до 273⁰С.

Решение

В данном случае , тогда

.

Задача 3Один моль идеального газа с показателем адиабатысовершает процесс по закону~, при этом абсолютная температура возрастает враз. Найти приращение энтропии газа а этом процессе.

Дано: ,,

Решение

. (1)

, учитывая, что, получим, тогда

,

,,

,.

Подставляя ,,в уравнение (1), получим

Задача 4Теплоизолированный сосуд разделен перегородкой на две части так, что объем одной из них враз больше объема другой. В меньшей части находитсямоля одного газа, а в большей частимоля другого газа. Температура газов одинакова. Перегородку удалили, газы перемешались. Найти приращение энтропиимакросистемы, считая газы идеальными.

Дано: ,,,

Решение

Из аддитивности энтропии следует, что , гдеинайдем, используя изотермический процесс расширения каждого газа.

Итак,

.

Имея в виду, что , получим

.

Задача 5Статистический весОдин моль идеального газа, состоящего из одноатомных молекул, находится в сосуде при температуре= 300 К. Как и во сколько раз изменится статистический вес этой макросистемы, если ее нагреть изохорически на= 1,0 К?

Решение

Учитывая, что

, имеем

.

Видно, что решение сводится к нахождению . Учитывая, что,, получим

.

В результате

.

Здесь учтено, что . Из последней формулы находим:

- величина грандиозная даже при таких скромных изменениях температуры.

Задача 6Цикл КарноОдин моль идеального газа из жестких двухатомных молекул совершает цикл Карно. Температура нагревателя= 400 К. Найти КПД цикла, если при адиабатическом сжатии затрачивается работа= 2,0 кДж.

Решение

При адиабатическом сжатии , следовательно,

,,

. Так как, поэтому

. Так как, то

, где=5 (двухатомная жесткая молекула).

Задача 7КПД циклаИдеальный трехатомный газ совершает цикл, состоящий из двух изохор и двух изобар. Определить КПД цикла, если= 1 л,= 2 л,= 1 атм,

= 2 атм.

Решение

КПД цикла равен

(1)

Работа газа , совершенная за цикл, численно равна площади фигуры, ограниченной замкнутой линией 1234 (рис.). Таким образом,

(2)

Количество тепла получено газом только при двух процессах:

а) изохорном на участке 1-2

б) изобарном на участке 2-3.

На участке 3-4 и 4-1 газ отдает тепло холодильнику .

Следовательно

, где,

(3)

Подставляя (3) и (2) в (1), получим

.

Учитывая, что для трехатомного газа = 6, получим= 0,09.

Задача 8Тепловой двигатель работает по циклу, состоящему из изотермического, изобарного и адиабатического процессов. При изобарном процессе рабочее тело – идеальный газ – нагревается от температуры= 200 К до= 500 К. Определить КПД двигателя.

Решение

В условии задачи не указана последовательность процессов, но поскольку изобарный процесс, по условию, - процесс нагревания, следовательно, и расширения, то изобара 1-2 должна лежать выше кривых, изображающих изотермический и адиабатический процессы (рис.).

(1)

- количество теплоты, получаемое рабочим телом при изобарном процессе,

(2)

Количество теплоты, отданное при изотермическом сжатии,

. (3)

Найдем .

Соотношения 1 и 2 лежат на одной изобаре:

. (4)

Состояния 2 и 3 лежат на одной адиабате:

.

Учитывая, что , получим

(5)

Перемножая равенства (4) и (5), имеем

.

Тогда

.

Так как , тои

(6)

Подставим (2) и (6) в (1):

Тесты

1. Чему равно приращение энтропии за цикл при обратимом процессе?

1.– приращению теплоты; 2. – приращению температуры; 3. – приращению энергии; 4. – нулю; 5. – бесконечности.

2. При стремлении абсолютной температуры к нулю энтропия системы стремится:

1. – к нулю; 2. – к бесконечности; 3. – остается постоянной; 4. – стремится к единице; 5. – становится неопределенной.

3. Максимальный термический коэффициент полезного действия теплового двигателя равен:

1. – ; 2. –; 3. –; 4. –; 5. –.T₁ – температура нагревателя; T₂ – температура холодильника.

4. Процесс, изображенный на рисунке в координатах (T,S), гдеS– энтропия, является…

1. – адиабатным расширением; 2. – изохорным охлаждением; 3. – изобарным сжатием; 4. – изотермическим сжатием.

5. Максимальный коэффициент полезного действия теплового двигателя равен:

1. – ; 2. –; 3. –; 4. –; 5. –.Q₁ – теплота, полученная от нагревателя; Q₂ – теплота, отданная холодильнику.

6. Оцените максимальное значение КПД, которое может иметь тепловая машина с температурой нагревателя 727°С и температурой холодильника 27°С.

1. – 70%; 2. – 100%; 3. – 30%; 4. – ≈ 43%; 5. – ≈ 96%.

7. Укажите размерность энтропии.

1. – ; 2. –; 3. –; 4. –; 5. –.

8. Цикл Карно состоит из:

1. – двух изотерм; 2. – двух адиабат; 3. – двух изотерм и двух адиабат; 4. – двух изотерм и двух изобар; 5. – двух адиабат и двух изохор.

9. Как изменяется энтропия при переходе системы из неравновесного в состояние термодинамического равновесия?

1. – ; 2. –; 3. –; 4. –; 5. –.

10. В каком случае к. п. д. цикла Карно повысится больше: 1 – при увеличении на Ттемпературы нагревателя или 2 – при уменьшении на такую же величинуТтемпературы холодильника?

1. – В случае 1; 2. – В случае 2; 3. – В обоих случаях одинаково; 4. – В случае 1 к. п. д. уменьшится; 5. – В случае 2 к. п. д. уменьшится.

11. Тепловая машина работает по циклу Карно. Если температуру нагревателя увеличить, то КПД цикла…

1. – не изменится; 2. – увеличится; 3. – уменьшится.

12. Процесс, изображенный на рисунке в координатах (T,S), гдеS– энтропия, является…

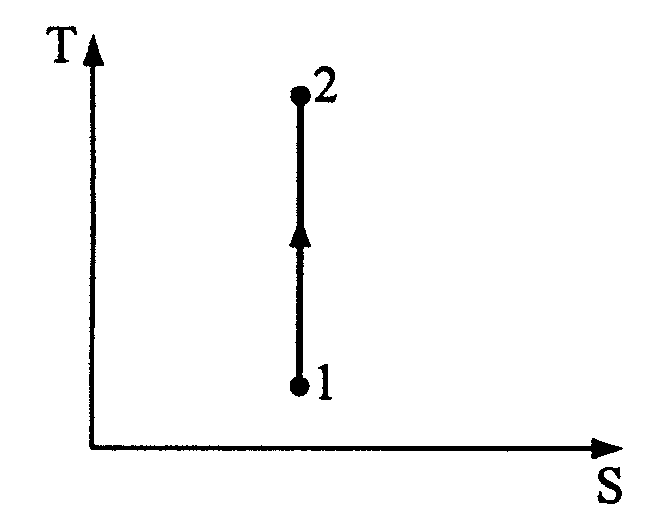
1. – изохорным нагреванием; 2. – адиабатным сжатием; 3. – изотермическим расширением; 4. – изобарным расширением.

13. На рисунке изображен цикл Карно в координатах (T,S), гдеS– энтропия. Изотермическое сжатие происходит на этапе…

1. 3 – 4; 2. 1 – 2; 3. 2 – 3; 4. 4 – 1.

14. На рисунке представлен цикл тепловой машины в координатах T,S, гдеT– термодинамическая температура,S– энтропия. Укажите нагреватели и холодильники с соответствующими температурами.

1. – Нагреватели – T₃, T₄, T₅; Холодильники – T₁, T₂.

2. – Нагреватели – T₂, T₄, T₅; Холодильники – T₁, T₃.

3. – Нагреватели – T₃, T₅; Холодильники – T₁, T₂, T₄.

4. – Нагреватели – T₄, T₅; Холодильники – T₁, T₂, T₃.

16