
- •9 Поле электрического диполя
- •10 Диполь во внешнем электростатическом поле
- •11 Ротор векторной функции и его физический смысл
- •Теорема Стокса
- •12 Уравнения электростатического поля в вакууме в интегральной и дифференциальной формах. Уравнение Пуассона. Уравнение Лапласа
- •1. Теорема Гаусса:
- •2. Теорема о циркуляции вектора :
- •Уравнение Пуассона
- •Уравнение Лапласа
ФИЗИКА
Модуль 2.5
9 Поле электрического диполя
Электрический диполь – это система
из двух одинаковых по модулю разноименных
точечных зарядов
![]() и
и
![]() ,
находящихся на некотором расстоянии
,
находящихся на некотором расстоянии
![]() друг друга, причем расстояние
друг друга, причем расстояние
![]() мало по сравнению с расстоянием
мало по сравнению с расстоянием
![]() до
тех точек, в которых рассматривается
поле системы (
до
тех точек, в которых рассматривается
поле системы (![]() ).
).
Прямая, проходящая через оба заряда,
называется осью диполя. Ориентацию
оси диполя в пространстве можно задать
с помощью вектора
![]() ,
проведенного от заряда
,
проведенного от заряда
![]() к заряду
к заряду
![]() .
.
Поле диполя обладает осевой симметрией, поэтому картина поля в любой плоскости, проходящей через ось диполя, одна и та же.
Найдем сначала потенциал поля диполя, а затем его напряженность. Согласно (1.39) потенциал поля диполя в точке Р (рис. 24) определяется как
![]()
Так как
![]() ,
то как видно из рис. 24
,
то как видно из рис. 24
![]() ,
а
,
а
![]() ,
где
,
где
![]() -
расстояние от точки Р до диполя (он
точечный!). С учетом этого
-
расстояние от точки Р до диполя (он
точечный!). С учетом этого
![]() , (1.52)
, (1.52)
где
![]() .
Этой величине
.
Этой величине
![]() сопоставляется
вектор
сопоставляется
вектор
![]() ,
который называют электрическим моментом
диполя или дипольным моментом.
,
который называют электрическим моментом
диполя или дипольным моментом.

Рис. 24
Из рис. 25 видно, что
![]() есть угол между моментом диполя
есть угол между моментом диполя
![]() и радиус-вектором
и радиус-вектором
![]() ,
поэтому формулу (1.52) можно записать в
виде:
,
поэтому формулу (1.52) можно записать в
виде:
![]() . (1.53)
. (1.53)
Отметим, что, в то время как потенциал
поля точечного заряда убывает как
![]() ,
потенциал поля диполя убывает с
расстоянием как
,
потенциал поля диполя убывает с
расстоянием как
![]() ,
т.е. гораздо быстрее.
,
т.е. гораздо быстрее.
Для нахождения поля диполя воспользуемся формулой (1.46), что
![]() .
.

Рис. 25
Вычислим с помощью этой формулы проекции
вектора
![]() на два взаимно перпендикулярных
направления – вдоль ортов
на два взаимно перпендикулярных
направления – вдоль ортов
![]() и
и
![]() (рис. 25).
(рис. 25).
![]() ,
,
![]() (1.54)
(1.54)
Отсюда модуль вектора
![]()
![]() (1.55)
(1.55)
В частности, при
![]() =0
мы получим выражение для напряженности
поля на оси диполя
=0
мы получим выражение для напряженности
поля на оси диполя
![]() :
:
![]() , (1.56)
, (1.56)
причем при
![]()
![]() .
Это означает, что на оси диполя
.
Это означает, что на оси диполя
![]() направлен вдоль оси. Согласно формуле
(1.54)
направлен вдоль оси. Согласно формуле
(1.54)
![]() при
при
![]() и
и
![]() при
при
![]() .
Отсюда следует, что в обоих случаях
направление вектора
.
Отсюда следует, что в обоих случаях
направление вектора
![]() .
(см. рис. 26).
.
(см. рис. 26).

Рис. 26
При
![]() мы получим выражение для напряженности
поля в точках плоскости, перпендикулярной
к оси диполя и проходящей через его
центр (
мы получим выражение для напряженности
поля в точках плоскости, перпендикулярной
к оси диполя и проходящей через его
центр (![]() ):
):
![]() , (1.57)
, (1.57)
причем при
![]()
![]() ,
а
,
а
![]() .
Это означает, что вектор
.
Это означает, что вектор
![]() антипараллелен вектору
антипараллелен вектору
![]() (см
рис. 26).
(см
рис. 26).
10 Диполь во внешнем электростатическом поле
Если диполь находится в однородном
электрическом поле, на его заряды
действуют равные по модулю, противоположно
направленные силы
![]() и
и
![]() (рис. 27). Эти силы образуют пару, плечо
которой равно
(рис. 27). Эти силы образуют пару, плечо
которой равно
![]() .
Модуль момента пары сил равен
.
Модуль момента пары сил равен
![]() , (1.58)
, (1.58)
где
![]() - модуль электрического момента диполя.
Вращающий момент
- модуль электрического момента диполя.
Вращающий момент
![]() перпендикулярен к векторам
перпендикулярен к векторам
![]() и
и
![]() ,
,
![]() - угол между векторами
- угол между векторами
![]() и
и
![]() .
Поэтому
.
Поэтому
![]() . (1.59)
. (1.59)
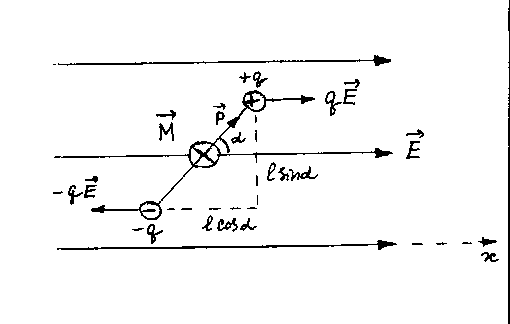
Рис. 27
Таким образом, однородное электрическое
поле оказывает на диполь ориентирующее
действие, стремясь установить его по
полю, т.е. чтобы
![]() .
Также положение диполя является
устойчивым.
.
Также положение диполя является
устойчивым.
Мы знаем, что энергия точечного заряда
![]() во внешнем поле равна
во внешнем поле равна
![]() ,
где
,
где
![]() - потенциал в точке нахождения заряда
- потенциал в точке нахождения заряда
![]() .
Энергия диполя во внешнем поле
.
Энергия диполя во внешнем поле
![]() ,
,
где
![]() и
и
![]() - потенциал внешнего поля в точках
расположения зарядов
- потенциал внешнего поля в точках
расположения зарядов
![]() и
и
![]() .
.
Потенциал однородного поля определяется выражением
![]() ,
,
где
![]() - ось, вдоль которой направлен вектор
- ось, вдоль которой направлен вектор
![]() .
.
Следовательно, энергия диполя равна:
![]() .
.
Здесь
![]() есть разность координат точек, в которых
находятся заряды
есть разность координат точек, в которых
находятся заряды
![]() и
и
![]() .
Из рис. 27 видно, что
.
Из рис. 27 видно, что
![]() .
Таким образом,
.
Таким образом,
![]()
или
![]() (1.60)
(1.60)
Формула (1.60) определяет потенциальную
энергию диполя с моментом
![]() ,
находящегося в поле с напряженностью
,
находящегося в поле с напряженностью
![]() .
.
Эта формула справедлива как для однородного, так и для неоднородного поля.
Из этой формулы следует, что минимальную
энергию (![]() )
диполь имеет в положении
)
диполь имеет в положении
![]() (положение устойчивого равновесия).
(положение устойчивого равновесия).
