46

3.Гидродинамические и восстанавливающие силы.

3.1Гидродинамические демпфирующие силы.

Гидродинамическое демпфирование МПО вызвано:

- наведенным потенциальным демпфированием от волновых воздействий;

- линейным трением о поверхностный слой от ламинарных пограничных потоков и квадратичным поверхностным трением от турбулентных пограничных потоков;

- демпфирование типа волновой дрейф;

- демпфирование от вихревых потоков при наличии шероховатости корпуса.

Соответственно, обобщенная матрица гидродинамического демпфирования представляет сумму указанных компонентов

, (3.1)

где удовлетворяет следующим свойствам:

вещественная, не симметричная и строго положительна и квадратичная форма

.

На практике обычно ограничиваются рассмотрением сил трения в поверхностном слое.

Общий вид матриц демпфирования.

Для надводных кораблей

Для низкоскоростных судов, двигающихся по прямой вдоль оси 0х в отсутствии вертикальной , боковой и килевой качек гидродинамические силыи моменты(можно записать

, причем;(3.2)

тогда

Для подводных аппаратов

В общем случае, демпфирование подводных аппаратов, двигающихся в пространстве [6DOF] с высокой скоростью будет существенно нелинейным. Тем не менее грубая аппроксимация для аппаратов имеющих три плоскости симметрии и при условии пренебрежения членами второго порядка малости допустима

(3.3)

Потенциальное демпфирование

Силы вызывающие вынужденные колебания с частотой набегающих волн могут быть связаны с присоединенными массами, демпфирующими силами и восстанавливающими силами и моментами (потенциальными силами Архимеда и веса). Волновые наведенные демпфирующие силы незначительны для аппаратов на большой глубине, однако для надводных кораблей они могут быть весьма значительны [4]. Расчет этих сил рассматривается в разделах связанных с расчетом качки.

Трение в поверхностном слое

Линейное трение в слое, в соответствии с теорией о ламинарном пограничном слое, важно при рассмотрении низкоскоростного движения МПО. Реальные объекты движутся с достаточно большими скоростями, что вызывает турбулентность в слое и трение рассматривается как нелинейное (обычно квадратичное) [4].

.

В этом случае проекции главного вектора и главного момента гидродинамических сил на оси связанной системы координат определяют следующим образом:

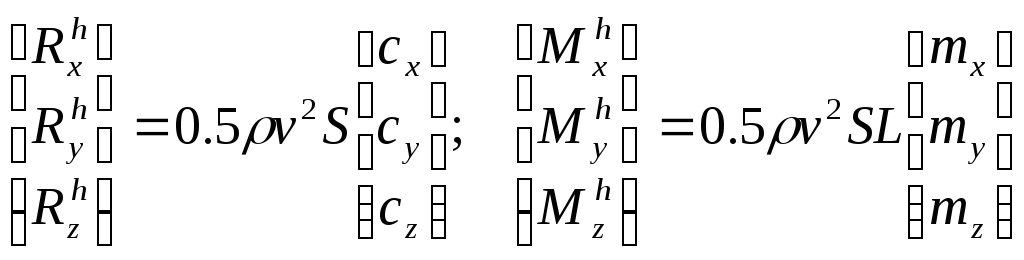. (3.4)

где-скорость потока жидкости, обтекающей корпус МПО,характерные площадь и длина МПО,- безразмерные характеристики или коэффициенты продольной, нормальной или поперечной гидродинамических сил;- безразмерные характеристики гидродинамических моментов крена, рыскания и дифферента.

Зачастую принимают .- объемное водоизмещение ОМТ (ПА).

Величины коэффициентов зависят от условий обтекания, формы корпуса и т.д. Их определяют с помощью упрощенных соотношений (формул Прандтля, например) или путем модельных испытаний в опытовых бассейнах и аэродинамических трубах. Для этого в определенном масштабе строят модели МПО, располагают их в динамометрическом подвесе и проводят с заданной скоростью в воде или обдувают воздухом в аэродинамических трубах. При этом фиксируют силы и моменты, действующие на модель МПО, а затем рассчитывают характеристики гидродинамических сил и моментов по формулам

, (3.5)

где - скоростной напор в бассейне или трубе;характерные площадь и длина модели.

Необходимыми условиями переноса на реальный МПО экспериментальных данных, полученных на модели, является условие геометрического и динамического подобия.

Для динамического подобия требуется равенство чисел Рейнольдса для модели и натурного объекта

.

Коэффициенты гидродинамических сил зависят от ориентации корпуса, условий обтекания, угловой скорости изменения положения МПО относительно потока

Примеры выражений для гидродинамических сил и моментов на корпусе при малых углах атаки и дрейфа

Проекции гидродинамических сил и моментов, действующих на корпусе ОМТ, определяются по следующим формулам:

(3.6)

где ;

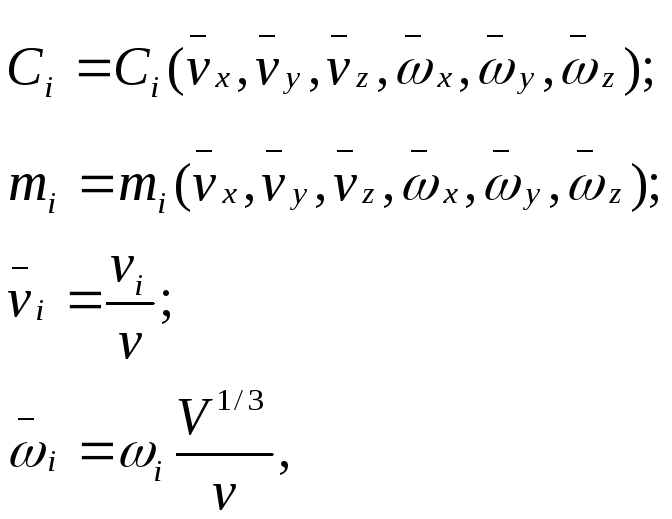
где i = x, y, z;