
- •ЛОГИЧЕСКИЕ
- •Булева алгебра
- •Логические высказывания
- •Обозначение высказываний
- •ПРИ СОЗДАНИИ ЭЛЕКТРОННЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИН БЫЛА ИСПОЛЬЗОВАНА НЕ ВСЯ СИСТЕМА, А ЧЕТЫРЕ ОСНОВНЫЕ
- •Операция НЕ (инверсия)
- •Операция И (логическое умножение, конъюнкция)
- •Операция ИЛИ (логическое сложение, дизъюнкция)
- •Операция "исключающее ИЛИ"
- •ОЧЕРЕДНОСТЬ ВЫПОЛНЕНИЯ ОПЕРАЦИЙ:
- •Свойства операции «исключающее ИЛИ»
- •Базовый набор операций
- •Логические формулы
- •Составление таблиц истинности
- •Составление таблиц истинности
- •Составление таблиц истинности
- •Составление таблиц истинности
- •Составление таблиц истинности
- •Составление таблиц истинности
- •Законы алгебры логики
- •Упрощение логических выражений
- •Синтез логических выражений
- •Синтез логических выражений (2 способ)
- •Синтез логических выражений
- •Синтез логических выражений (2 способ)
- •Логические элементы компьютера
- •Логические элементы компьютера
- •Составление схем
- •Триггер (англ. trigger – защёлка)
- •Полусумматор
- •Сумматор
- •Многоразрядный сумматор

Упрощение логических выражений
Шаг 1. Заменить операцию на её выражение через
И, ИЛИ и НЕ:
A B A B A B
Шаг 2. Раскрыть инверсию сложных выражений по формулам де Моргана:
A B A B, A B A B
Шаг 3. Используя законы логики, упрощать выражение, стараясь применять закон исключения третьего.
21
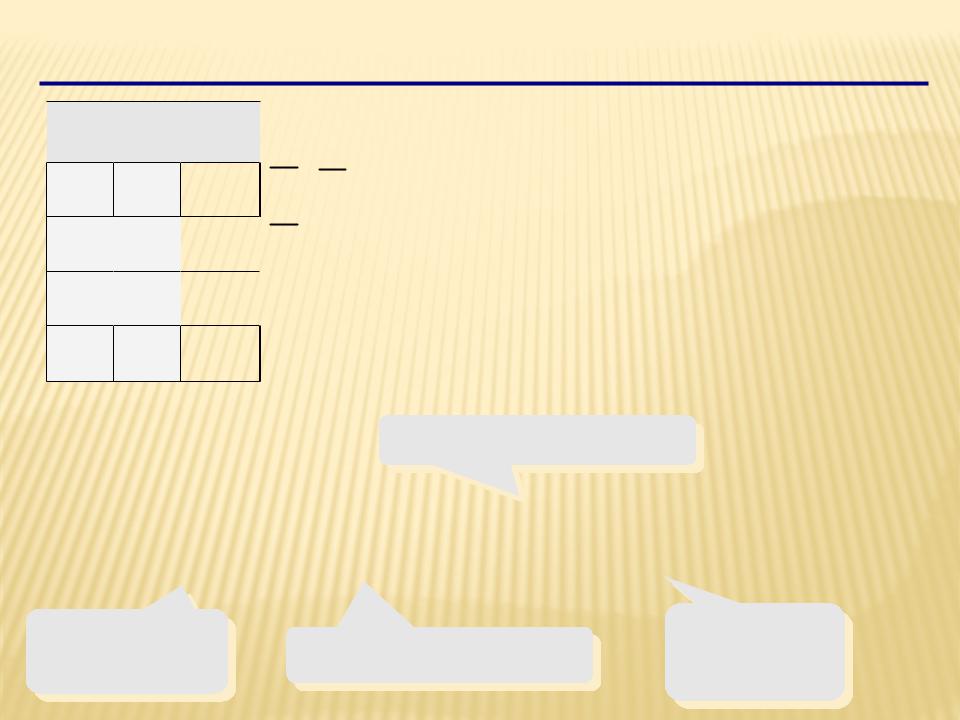
Синтез логических выражений
 A
A  B
B  X
X 
0 0 1 A B
A B
0  1
1  1
1
 A B 1
A B 1  0
0  0
0 
1 1 1 A B
A B
Шаг 1. Отметить строки в таблице, где X = 1.
Шаг 2. Для каждой из них записать логическое выражение, которое истинно только для этой строки.
Шаг 3. Сложить эти выражения и упростить результат.
распределительный
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A B |
|
A |
B |
A B |
|
|
|
|
||||||||||
|
|
A) ( |
|
B) |
|
B |
||||||||||
|
A |
A B ( |
|
|
A |
|||||||||||
A |
A |
|||||||||||||||
исключения |
|
|
|
распределительный |
|
|
|
исключения |
||||||||
третьего |
|
|
|
|
|
|
|
третьего |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
22
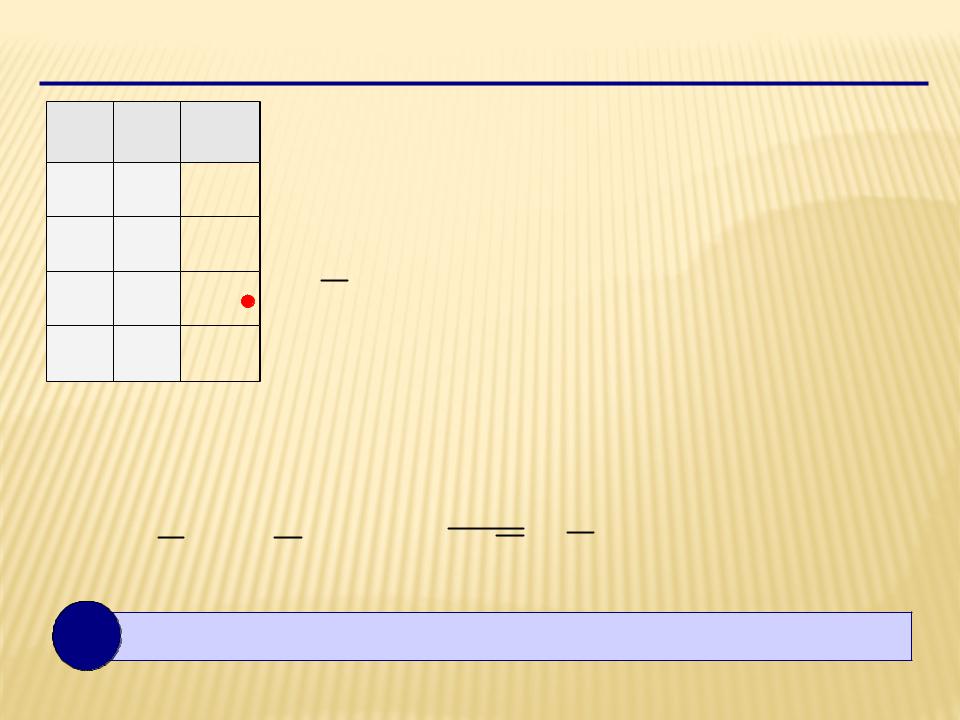
Синтез логических выражений (2 способ)
A |
B |
X |
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
0 |
A B |
1 |
1 |
1 |
|
Шаг 1. Отметить строки в таблице, где X = 0.
Шаг 2. Для каждой из них записать логическое выражение, которое истинно только для этой строки.
Шаг 3. Сложить эти выражения и упростить результат, который равен X .
Шаг 4. Сделать инверсию.
X A B X A B A B
? Когда удобнее применять 2-ой способ?
23
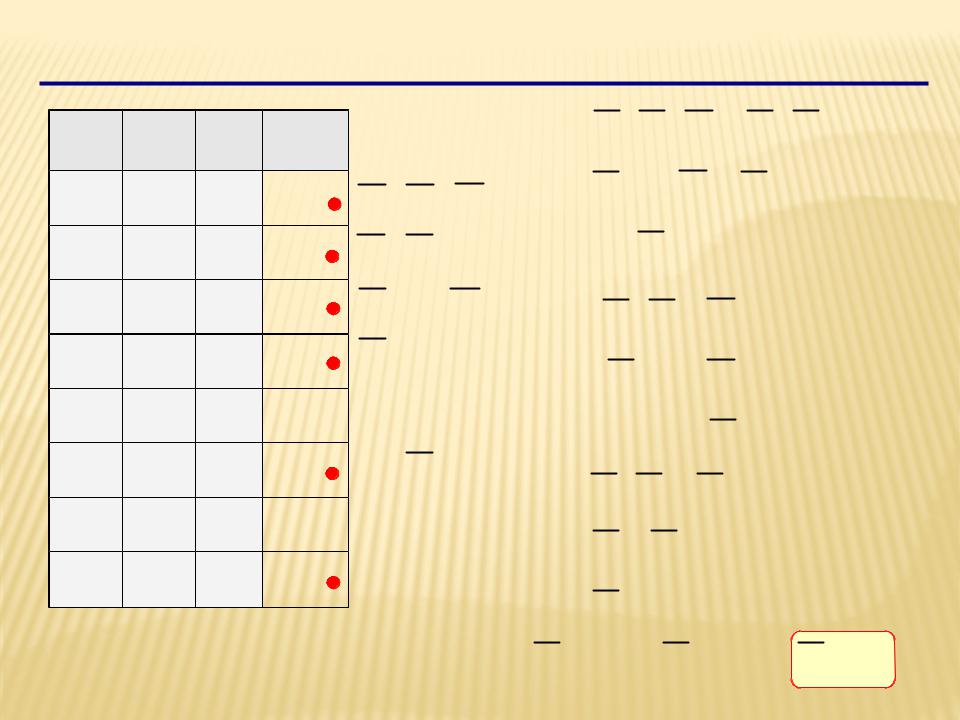
Синтез логических выражений
A |
B |
C |
X |
|
0 |
0 |
0 |
1 |
A B C |
0 |
0 |
1 |
1 |
A B C |
0 |
1 |
0 |
1 |
A B C |
0 |
1 |
1 |
1 |
A B C |
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
A B C |
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
A B C |
XA B C A B C
A B C A B C
A B C A B C
A B (C C)
A B (C C)
A C (B B)
A B A B A C
A (B B) A C
A A C
(A A) (A C) A C
24
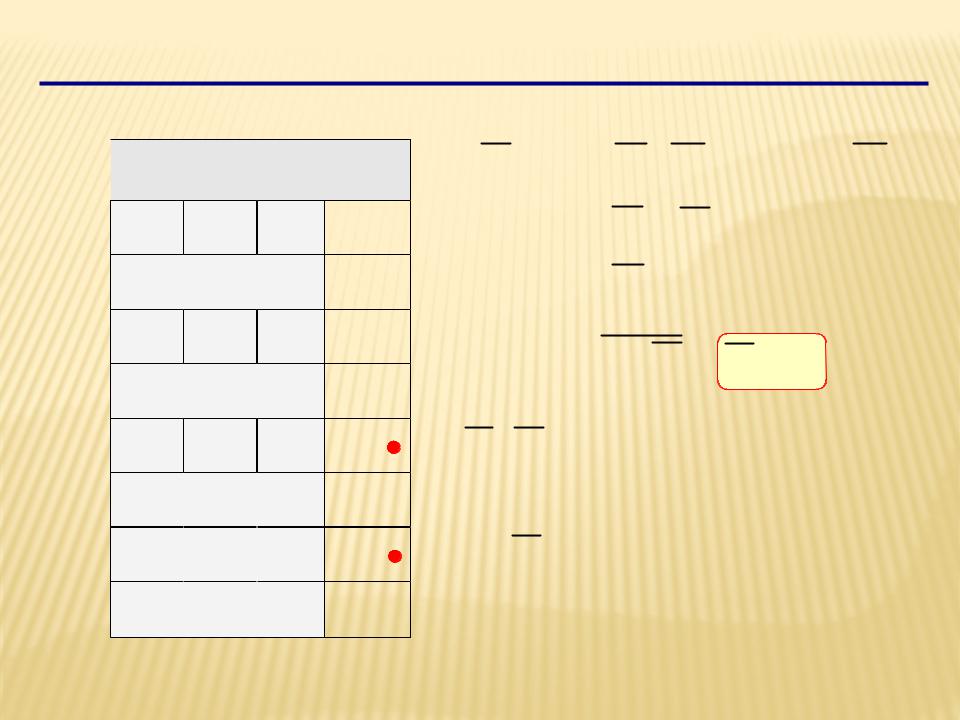
Синтез логических выражений (2 способ)
 A
A  B
B  C
C 
0 0 0
0  0
0  1
1
0 1 0
0  1
1  1
1
1 0 0
1  0
0  1 1
1 1  1
1  0 1
0 1  1
1  1
1
X |
X A B C A B C |
|
1 |
A C (B B) |
|
1 |
A C |
|
1 |
X A C A C |
|
1 |
||
|
||
0 |
A B C |
|
1 |
|
|
0 |
A B C |
|
1 |
|
25

Логические элементы компьютера
значок инверсии
A |
|
A B |
A |
1 |
A B |
|
|
||||
|
|
|
|||
|
|
B |
B |
|
|
|
НЕ |
И |
|
ИЛИ |
|
|
|
|
|
A |
& A B |
A |
1 |
A B |
|
B |
B |
||||
|
|
|
|||
|
И-НЕ |
|
ИЛИ-НЕ |
|
26
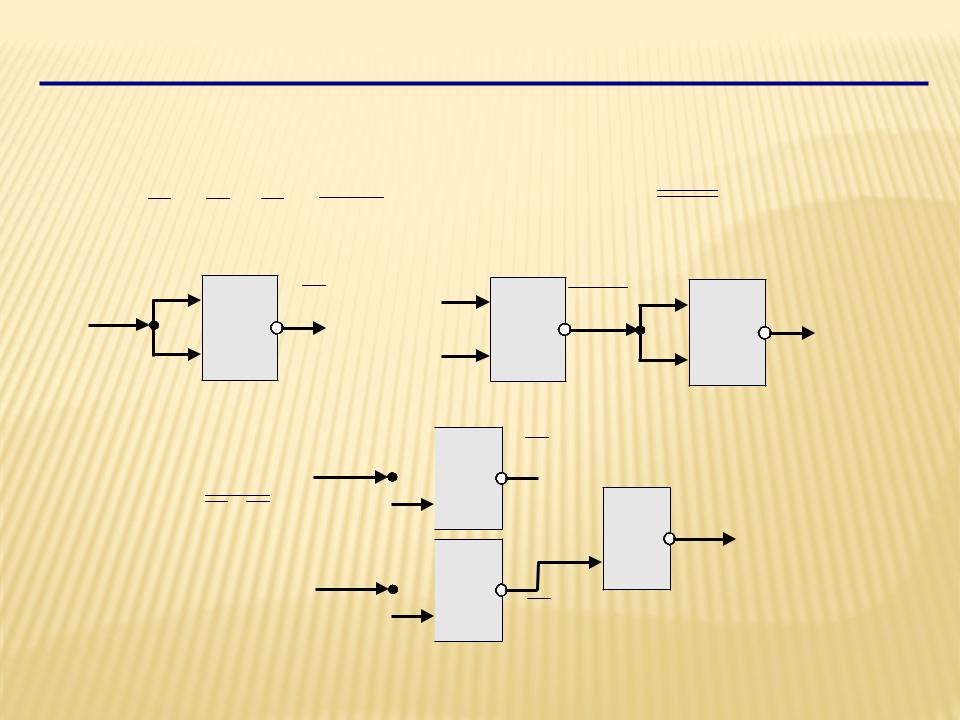
Логические элементы компьютера
Любое логическое выражение можно реализовать на элементах И-НЕ или ИЛИ-НЕ.
НЕ: A A A A A |
|
И: A B A B |
|
|
A |
& A |
A |
& A B & |
A B |
|
|
B |
|
|
ИЛИ: A
A B A B
B

 &
&

 &
&
A

 & A B
& A B
B
27
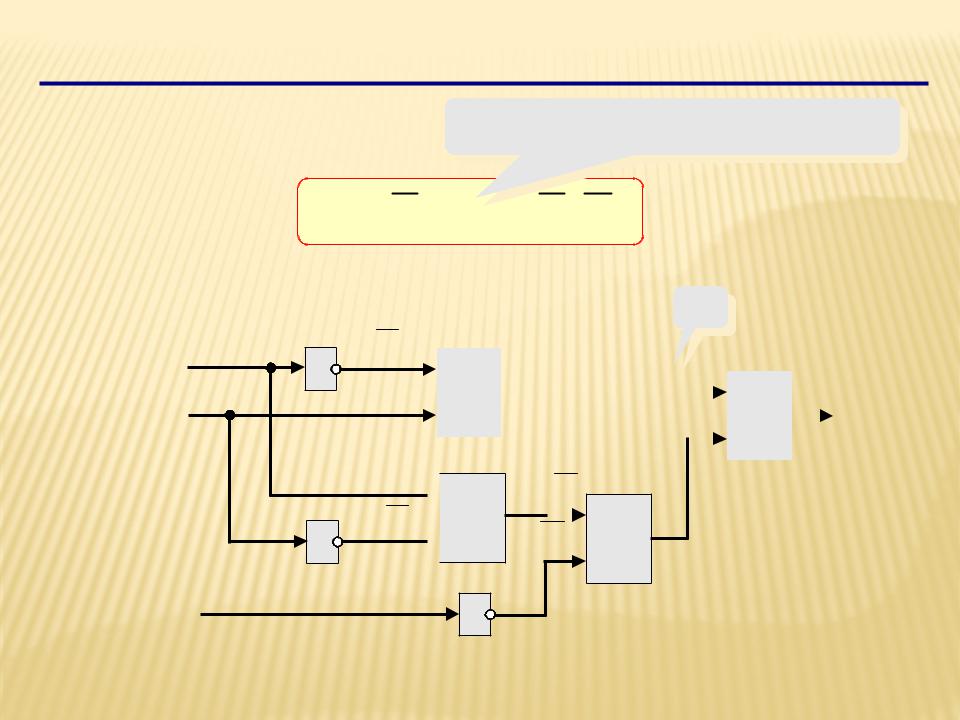
Составление схем
последняя операция - ИЛИ
X A B A B C
A |
A |
|
B |
||
B |
||
|
||
|
A |
|
|
B |
C
И
& |
|
|
|
A |
|
|
|
|
|
|||
|
|
|
|
1 |
|
X |
||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
A B C |
|
|
|||||||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
 & ACB &
& ACB &
28
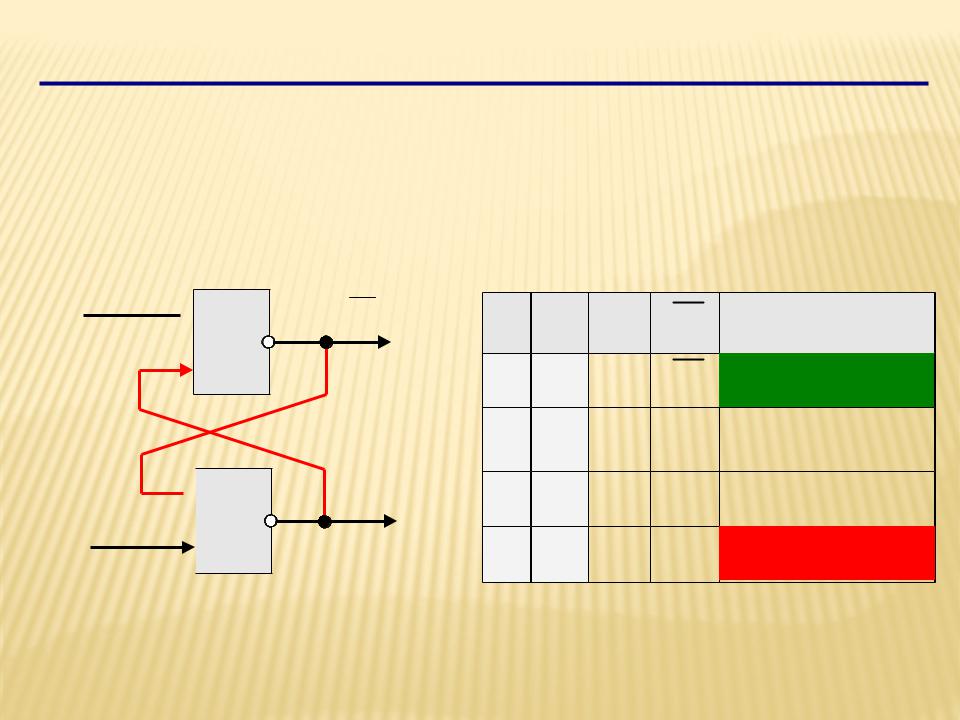
Триггер (англ. trigger – защёлка)
Триггер – это логическая схема, способная хранить 1
бит информации (1 или 0). Строится на 2-х элементах ИЛИ-НЕ или на 2-х элементах И-НЕ.
set, установка
S
 1
1
 1
1
R
reset, сброс
вспомогательный
выход
Q |
S R Q |
Q |
||
|
0 |
0 |
Q |
Q |
обратные связи |
0 |
1 |
0 |
1 |
|
||||
Q |
1 |
0 |
1 |
0 |
основной |
1 |
1 |
0 |
0 |
выход |
|
|
|
|
режим
хранение
сброс
установка 1
запрещен
29
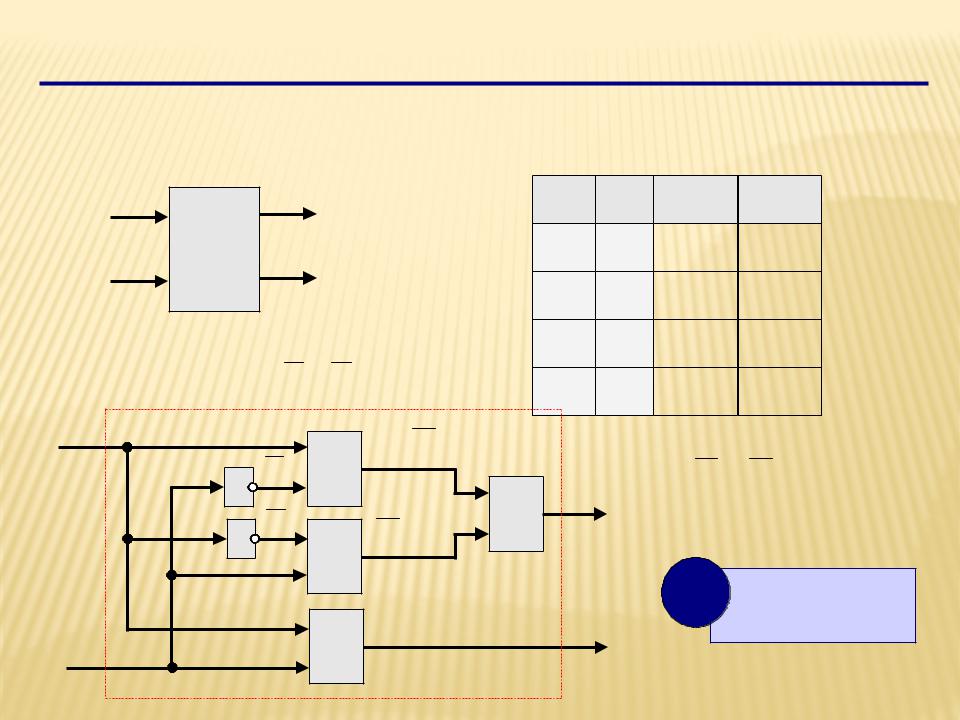
Полусумматор
Полусумматор – это логическая схема, способная складывать два одноразрядных двоичных числа.
A |
Σ |
S сумма |
|
A |
B |
P |
S |
|
|
P перенос |
0 |
0 |
0 |
0 |
|||
B |
|
|||||||
|
0 |
1 |
0 |
1 |
||||
|
|
|
|
|
||||
P A B |
|
|
|
1 |
0 |
0 |
1 |
|
S A B A B A B |
1 |
1 |
1 |
0 |
||||
A |
|
|
|
|
|
|
||
|
|
& A B |
|
|
|
|
||
|
|
B |
1 |
S A B A B |
||||
|
|
|
|
|||||
|
|
A |
& A B |
|
|
|
||
|
|
|
|
|
Схема на 4-х |
|||
B |
|
|
& |
A B |
|
P |
? элементах? |
|
|
|
|
|
|
|
|||
30
