2. В умозаключении пропущена одна из посылок

В умозаключениях может быть пропущена первая посылка, она может подразумеваться, если выражает какое-то истинное суждение, формулирующее известное положение, теорему, за­кон и т. д.

В условно-категорическом умозаключении “Сумма цифр данного числа делится на 3, следовательно, данное число де­лится на З” опущена первая посылка, формулирующая извест­ную математическую закономерность: “Если сумма цифр дан­ного числа делится на 3, то все число делится на З”.

176

В разделительно-категорическом умозаключении “Данное су­ществительное русского языка не является существительным ни женского рода, ни среднего рода. Следовательно, данное существительное мужского рода” также пропущена первая посылка: “Существительное в русском языке может быть жен­ского, или мужского, или среднего рода”.

В сложной конструктивной дилемме “Если я пойду через бо­лото, то могу попасть в трясину, а если я пойду в обход, то не успею вовремя доставить донесение. Следовательно, я могу попасть в трясину или не успею вовремя доставить донесение” не формулируется, а лишь подразумевается вторая посылка: “Я могу идти через болото или в обход”.

Можно было бы привести и другие примеры сокращенных умо­заключений: чисто условных, условно-категорических, чисто раз­делительных, разделительно-категорических, условно-раздели­тельных (дилемм, трилемм) с пропущенной или первой, или вто­рой посылкой, однако предоставим это сделать самому читателю.

Итак, рассмотренные нами прямые выводы - такие, как чи­сто условные, чисто разделительные, условно-категорические, разделительно-категорические и условно-разделительные (лемматические) умозаключения, сформулированные как полностью, так и сокращенно (т. е. в которых пропущена либо одна из посы­лок, либо заключение), - широко используются в процессах на­учного и обыденного мышления, обучения в школе или в вузе. Знание правил построения этих видов умозаключений предосте­регает от логических ошибок в мышлении, помогает доказатель­нее, аргументированное строить рассуждения и эффективнее применять приемы обучения учащихся и студентов.

Прямые выводы (кроме рассмотренных выше форм) вклю­чают и такие виды (делаемые из одной посылки):

1. Простая контрапозиция.

Правило простой контрапозиции имеет следующий вид:

177

Это правило читается так: “Если а имплицирует, то отрицание b имплицирует отрицание а”. Здесь а и b – переменные, обозначающие произвольные высказывания, или пропозициональные переменные.

Примеры:

1. Если данный треугольник равносторонний, то он равноугольный.

Если данный треугольник не равноугольный, то он не равносторонний.

2) Если это вещество фосфор, то оно непосредственно с водородом не со­единяется.

Если вещество непосредственно с водородом соединяется, то это вещест­во не является фосфором.

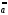
Заметим, что в логике высказываний а. Формула:

(а→ b) () называется законом простой контрапозиции.

2. Сложная контрапозиция.

- правило сложной контрапозиции.

((a ^ b) → с) ((а^ с) ) - это формула закона сложной контрапозиции.

Пример рассуждения по правилу сложной контрапозиции:

Если у меня будут деньги и я буду здорова, то я на каникулы поеду домой.

Если у меня были деньги и я на каникулы не поехала домой, то, следователь­но,

я не была здорова.

3. Правило импортации (конъюнктивного объединения условий).

Видный математик П. С. Новиков назвал данное правило пра­вилом соединения посылок.

Это правило читается так: “Если а имплицирует, что b имп­лицирует с, то а и b имплицируют с”.

В. А. Сухомлинский писал: “Если учитель стал другом ребен­ка, если эта дружба озарена благородным увлечением, порывом

178

к чему-то светлому, разумному, в сердце ребенка никогда не появится зло”. На основании правила соединения посылок (пра­вила коньюктивного объединения условий) мы можем это выска­зывание В. А. Сухомлинского записать иначе, но оно будет экви­валентно прежнему его высказыванию: “Если учитель стал дру­гом ребенка и эта дружба озарена благородным увлечением, порывом к чему-то светлому, разумному, то в сердце ребенка никогда не появится зло”.

4. Правило экспортации (разъединения условий).

Это правило читается так: “Если а и b имплицируют с, то а имплицирует, что b имплицирует с”. Это правило обратно пре­дыдущему. Поэтому в качестве иллюстрации можно взять те же мысли В.А. Сухомлинского, только сначала прочитать нашу запись полученного заключения, откуда можно прийти к выска­зыванию самого В. А. Сухомлинского.

Приведем другой, более сложный пример, иллюстрирующий правило экспортации (разъединения условий), в котором сформу­лированы не два, а четыре условия: “Если вы любите детей, пол­ны жажды познания, имеете доброе сердце, мечтаете посвятить себя интересному творческому труду, то смело выбирайте про­фессию учителя”. Формула этого сложного суждения такая:

(a^b^c^d)→е.

На основании правила экспортации имеем:

Сформулируем предыдущее суждение по-другому, но эквива­лентным образом: “Если вы любите детей, если полны жажды познания, если имеете доброе сердце, если мечтаете посвятить

179

себя интересному творческому труду, то смело выбирайте профессию учителя”.