Тема 11. Случайные величины и их числовые характеристики.

Основные вопросы теории.

1. Понятие случайной величины. Дискретные и непрерывные случайные величины. Закон распределения вероятностей дискретной случайной величины. Аналитический, табличный и графические способы задания закона распределения вероятностей дискретной случайной величины.

2. Понятие о законе распределения вероятностей непрерывной случайной величины. Плотность вероятности. Нормальное распределение случайной величины.

3. Числовые характеристики случайной величины. Вероятностный смысл математического ожидания. Математическое ожидание числа появлений события в независимых испытаниях. Свойства математического ожидания.

4. Дисперсия как мера рассеяния значений случайной величины. Способы вычисления дисперсии дискретной случайной величины. Дисперсия числа появления события в независимых испытаниях. Свойства дисперсии. Среднее квадратическое отклонение.

5. Числовые характеристики случайной величины, распределённой по нормальному закону, вероятность ее попадания в заданный интервал.

Примеры решения задач

Задача 23

Задан закон распределения вероятностей дискретной случайной величины:

xi	-1	0	2	4	7
pi	0,1	0,2	0,3	0,3	0,1

Вычислить: 1) математическое ожидание

2) дисперсию

3) среднее квадратическое отклонение, изобразить закон распределения графически и показать на чертеже вычисленное математическое ожидание.

Решение.

1. Математическое ожидание дискретной случайной величины вычисляется по формуле:

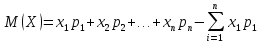
Подставляя данные из таблицы в формулу получаем:

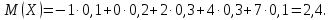
2. Дисперсия дискретной случайной величины равна по определению:

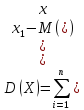
но ее удобнее вычислить по формуле

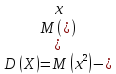
Вычислим

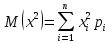
M(x²)=(-1)²·0,1+0²·0,2+2²·0,3+4²·0,3+7²·0,1=0,1+1,2+4,8+4,9=11,0.

Тогда D(X)=11,0-(2,4)²=11,0-5,76=5,24.

3. Среднее квадратическое отклонение

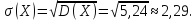
4. Для графического изображения закона распределения в виде многоугольника распределения на оси абсцисс откладываем возможные значения случайной величины, по оси ординат – вероятности этих значений; полученные точки соединяем отрезками прямых.

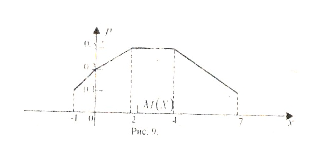
Вычисленное значение математического ожидания откладываем от начала координат по оси абсцисс.

Задача 24.

Вес плода – случайная величина, распределённая по нормальному закону с математическим ожиданием 5г и средним квадратическим отклонением 0,4г.

Определить: 1) процент плодов, вес которых заключён между 4г и 5,5г;

2) процент плодов, имеющих вес свыше 4,5г;

3)величину, которую не привысит вес плода с вероятностью 0,95.

Решение.

Пусть непрерывная случайная величина Х – вес плода.

1. Вероятность попадания на заданный интервал (α,β) непрерывной случайной величины Х, подчинённой нормальному закону с параметрами α, σ, т.е. ХϵN(α,σ), вычисляются по формуле:

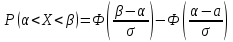
Где 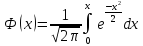- функция Лапласа, а=М(Х), σ=σ(Х).

В этой задаче а=М(Х)=5г. σ=σ(Х)=0,4г, α=4г, β= 5,5г, поэтому

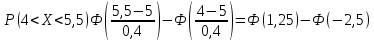
В силу нечётности функции Лапласа Ф(-2,5)=-Ф(2,5). По таблице 2 приложения находим Ф(1,25)=0,3944, Ф(2,5)=0,4938.

Таким образом, Р(4<X<5,5)=0,3944+0,4938=0,8822.

Итак 88,82% плодов имеют вес от 4г до 5,5т

2. Требуется найти вероятность того, что случайная величина Х примет значения, больше 4,5г.

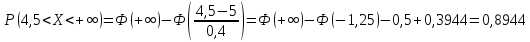
Здесь использован тот факт, что функция Лапласа Ф(х)=0,5, если х>5, т.е. Ф(+∞)=0,5.

Следовательно 89,44% плодов имею вес свыше 4,5г.

3. Обозначим искомую величину ϒ. Находим ее из условия Р(Х<ϒ)=0,95 или Р(-∞<Х<ϒ)=0,95. Выражение для вероятности в левой части равенства запишем через функцию Лапласа:

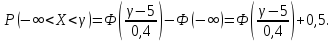
Итак, 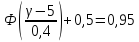, отсюда находим значение функции Лапласа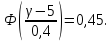

По таблице 2 приложения находим значение аргумента, при котором значение функции Ф(х) равно 0,45;

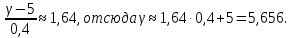
Таким образом, вес наугад взятого плода не будет превышать 5,656г с вероятностью 0,95.