Тема 10. Повторные испытания.

Основные вопросы теории.

1.Повторные независимые испытания. Схема испытаний Бернулли. Биноминальное распределение вероятностей. Формулы Бернулли. Определение наивероятнейшего числа появлений события.

2.Локальная и интегральная теоремы Муавра – Лапласа. Формула Пуассона. Области применения биномиального распределения вероятностей.

Примеры решения задач.

Задача 20

В бурте картофеля имеется 10% клубней, поражённых болезнью. Каковы вероятности того, что из пяти взятых наугад клубней:

1. ни один не будет поражён болезнью;

2. окажется только два клубня поражённых болезнью;

3. будет не более одного клубня поражённого болезнью?

Решение.

Вероятность того, что наугад взятый клубень поражён болезнью 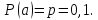вероятность того, что клубень здоровый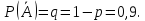

1). Обозначим событие В - пять клубней не поражены болезнью. Тогда 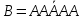и

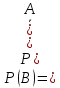
Используя формулу Бернулли 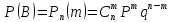, где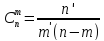,p=0,1, q=0,9, m=0, n=5, получим тот же результат

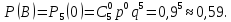
2). Пусть С – событие, состоящее в том, что два клубня из пяти поражены болезнью. Здесь n=5, m=2, p=0,1, q=0,9 и по формуле Бернулли

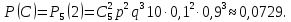
3). Пусть теперь событие D состоит в том, что из пяти клубней поражённых болезнью клубней будет не более одного. Это событие может быть представлено в виде суммы двух событий:

D₀ – все пять клубней здоровы (0 поражённых клубней);

D₁ – из пяти клубней лишь один поражён болезнью (а четыре – здоровы), т.е. D=D₀+D₁, где D₀и D₁–несовместные.

Вероятности событий D₀и D₁ получаем по формуле Бернулли:

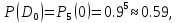
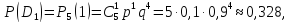
поэтому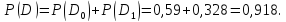

Задача 21.

Вероятность изготовления нестандартной тракторной детали равна 0,003. Найти вероятность того, что в партии из 1000 деталей окажется 4 нестандартные.

Решение

Проводится ряд повторных независимых испытаний изготовление деталей для тракторов. Число испытаний n=1000. В каждом испытании вероятность появления нестандартной детали равна р=0,003. Требуется найти Р₁₀₀₀(4). Так как вероятность р близка к 0, а число испытаний очень велико, то для решения задачи применим формулу Пуассона для редких событий:

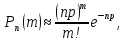
np=1000∙0,003=3, m=4,

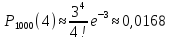
Задача 22.

При сортировке персиков вероятность того, что наудачу взятый персик не соответствует стандарту, составляет 0,2. Каковы вероятности того, что из наугад взятых 500 персиков: 1) окажутся нестандартными 90 штук; 2) нестандартных будет не менее 85, не более 110 штук.

Решение.

1). При больших значениях числа испытаний n вычисление вероятностей P_n(m) по формуле Бернулли становится очень трудным. В этом случае удобно пользоваться локальной формулой Муавра – Лапласа: 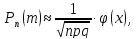где.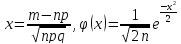

Значения функции 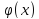определяются по таблице №1 (см. приложение). При этом нужно помнить, что функция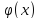четная, т.е..

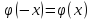По условию задачи

n=500, m=90, h=0,2, q=1-p=0,8.

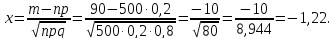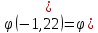Тогда По таблице 1 приложения находим1,12)=0,2131. Тогда искомая вероятность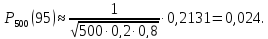

2). Если нужно вычислить вероятность того, что некоторое событие при большом количестве n повторных независимых испытаний произойдёт не ровно m раз, а не менее m₁и не более m₂ раз, то можно пользоваться интегральной формулой Муавра – Лапласа:

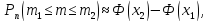
где

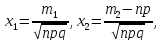
Значение функции Лапласа Ф(х) определяются по таблице №2 (см. приложение). При этом нужно помнить, что функция Ф(х) нечётная, т.е. Ф(-х)=-Ф(х), и при х>5 Ф(х)=0,5.

По условию задачи

n=500, m₁=85, m₂=110, p=0,2, q=0,8,

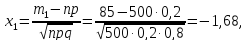
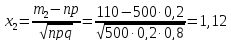
По таблице 2 приложения находим:

Ф(-1,68)=-Ф(1,68)=-0,4535, Ф(1,12) =0,3686

Тогда исходная вероятность