Тема 8. Основные понятия теории вероятностей.

Основные вопросы теории.

1. Предмет теории вероятностей. Понятие события. Классификация событий.

2. Относительная частота появления события, ее устойчивость. Вероятность события.

3. Классическая формула для вычисления вероятности события. Формулы комбинаторики.

Примеры решения задач.

Задача 16.

В ящике 250 яиц, из которых 15 бракованных. Из ящика одно за другим вынимают наудачу два яйца. Найти:

1. Вероятность того, что первое вынутое яйцо будет небракованным;

2. Вероятность того, что второе яйцо будет бракованным, если первое яйцо оказалось небракованным.

Решение:

Здесь можно использовать классическое определение вероятности: вероятность события А равна отношению числа исходов m, благоприятствующих наступлению данного события, к общему числу n всех исходов испытания (несовместных и равновозможных), т.е. .

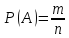1. Пусть А – событие, состоящее в том, что первое яйцо окажется небракованным. Число всех возможных исходов n=250, т.к. извлечение любого из 250 яиц одинаково возможно. Число исходов, благоприятствующих событию А, равно m = 250-15=235, т.к. из 250 яиц 15 бракованные, а 235 небракованные. Искомая вероятность события А равна:

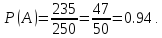
2. Обозначим событие В – навлечённое, вторым яйцо оказалось бракованным, если первое яйцо было небракованным. Число возможных исходов n=249, т.к. одно яйцо уже взято. Число исходов, благоприятствующих событию В. m=15

Итак: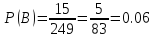

Тема 9. Теоремы о вероятности суммы и произведения событий.

Основные вопросы теории

1. Сумма и произведение событий.

2. Вероятность суммы несовместных и совместных событий.

3. Условная вероятность события. Вероятность произведения зависимых и независимых событий.

Примеры решения задач.

Задача 17

Мастер обслуживает пять станков 25% рабочего времени он работает у первого станка, 15% - у второго, 10% - у третьего, 20% - у четвёртого, 30% - у пятого.

Найти вероятность того, что в наудачу выбранный момент времени мастер находится: 1) у первого или третьего станка, 2) у второго или пятого станка, 3) у первого, или второго, или четвёртого станка.

Решение.

Обозначим А₁,А₂,А₃,А₄,А₅ – события, которые состоят в том, что в наудачу выбранный момент времени мастер находится соответственно у первого, второго, третьего, четвёртого, и, наконец, пятого станка. Из условия задачи следует, что эти события попарно несовместимы и

P(A₁)=0,25; P(A₂)=0,15; P(A₃)=0,10; P(A₄)=0,20; P(A₅)=0,30;

1). Событие, которое состоит в том, что мастер находится у первого или третьего станка, - это сумма событий А₁+А₃. Надо найти P(A₁+A₃). По теореме вероятности суммы несовместных событий

P(A₁+A₃)=P(A₁)+P(A₃)=0,25+0,10=0,35.

Аналогично

2). P(A2+A5)=P(A2)+P(A5) = 0,15+0,30=0,45.

3). P(A1+A2+A4)=P(A1)+P(A2)+P(A4)=0,25+0,15+0,20=0,60

Задача 18.

Три трактора работают независимо друг от друга. Вероятность бесперебойной работы первого трактора в течение некоторого времени t равна р₄=0,9, второго – р₂=0,8, третьего – р₃=0,75.

Найти вероятности:

1). Бесперебойной работы всех тракторов в течении указанного промежутка времени.

2). Бесперебойной работы хотя бы одного трактора в течении времени t.

3). Бесперебойной работы только одного трактора в течении этого времени.

Решение.

Рассмотрим следующие события: А₁,А₂ и А₃ – бесперебойная работа соответственно первого, второго и третьего тракторов в течение времени t.

1). Пусть событие А – бесперебойная работа тех тракторов в течение указанного времени. Тогда событие А есть произведение событий А₁,А₂,А_3. т.е. А=А₁·А₂·А₃. Так как события А₁,А₂ и А₃ независимы, то по теореме о вероятности произведения независимых событий

P(A)=P(А₁·А₂·А₃)= P(А₁)·P(А₂)·P(А₃)= 0,9·0,8·0.75=0,54.

2). Пусть событие В – бесперебойная работа хотя бы одного из тракторов в течение времени t. рассмотрим противоположное событие 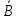, обозначающее простой всех тракторов в течение этого времени. Очевидно, что событие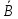есть произведение событи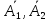йи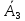– простоев первого, второго и третьего тракторов, т.е.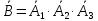и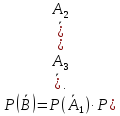

Так как сумма вероятностей противоположных событий равна

1. т.е.

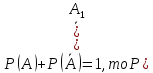
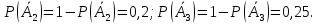
Поэтому

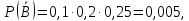
а поскольку 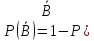), то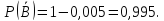

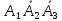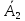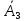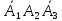3). Пусть событие С – бесперебойная работа только одного трактора в течении времени t. Событие С происходит, когда имеет место одно из следующих трех несовместных событий: либо произведение событий А₁, и(первый трактор работает, а второй и третий не работают), либо(первый и третий тракторы не работают, а второй работает), либо

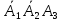(работает третий трактор и не работают остальные), т.е.

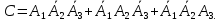
По теоремам о вероятности суммы несовместных и произведения независимых событий получим:

Р(С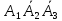)=Р(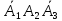)+Р()+Р()=++=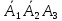

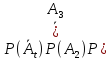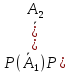=0,9·0,2·0,25+0,1·0,8·0,25+0,1·0,2·0,75=0,08.

Задача 19.

Многолетними наблюдениями установлено, что в данной местности в сентябре 10 дней бывают дождливыми. Хозяйство должно в течение первых трех дней сентября выполнить определённую работу. Определить вероятность того, что ни один из этих дней не будет дождливым.

Решение.

Пусть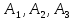– события, состоящие в том, что соответственно первый, второй и третий день сентября не будет дождливым, а А-событие, заключающееся в том, что в течение первых трех дней сентября не будет дождя. Тогда А является произведением зависимых событий: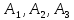

А=.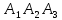

По теореме о вероятности произведения зависимых событий имеем:

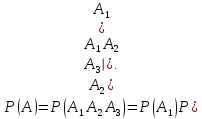
Так как в сентябре 30 дней, то число всех возможных исходов n=30, а событию А₁ из них благоприятствуют m=30-10=20 исходов.

Итак, .

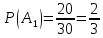Условная вероятность того, что второй день сентября не будет дождливым при условии, что первого сентября дождя не было, равна 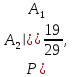т.к. при этом условии число возможных исходовn=30-1=29, а благоприятных m=20-1=19.

Аналогично, условная вероятность того, что 3 сентября дождя не будет, если его не было предыдущие два дня, равна

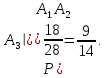
Следовательно