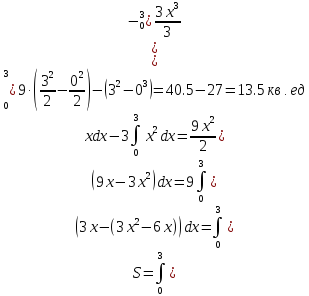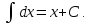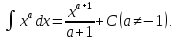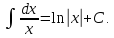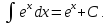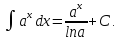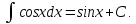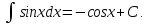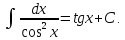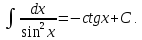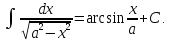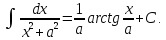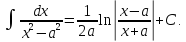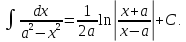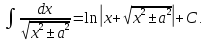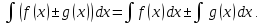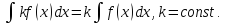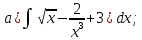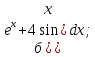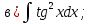- •Методические указания и контрольные работы
- •Тема 1. Определители и системы линейных алгебраических уравнений.
- •Тема 2. Элементы аналитической геометрии на плоскости.
- •Тема 3. Введение в математический анализ.
- •Тема 4. Производная и дифференциал функции.
- •Тема 5. Применение производной к исследованию функций.
- •Тема 6. Неопределенный интеграл.
- •Тема 7. Определённый интеграл.
- •Тема 8. Основные понятия теории вероятностей.
- •Тема 9. Теоремы о вероятности суммы и произведения событий.
- •Тема 10. Повторные испытания.
- •Тема 11. Случайные величины и их числовые характеристики.
- •Тема 12. Основные сведения из математической статистики.
- •Тема 13. Статистические оценки параметров распределения.
- •Тема 14. Корреляционная зависимость.
Тема 6. Неопределенный интеграл.
Основные вопросы теории.
Первообразная функция и неопределенный интеграл. Основные свойства неопределенного интеграла. Таблица основных интегралов.
Основные методы интегрирования.
Для справок приводим таблицу основных интегралов
Свойства неопределенного интеграла:
Примеры решения задач.
Задача 13. Найти интегралы:
|
|
|
|
|
|
Решение.
а) Преобразуем подынтегральную функцию, введя дробные и отрицательные показатели степени( см.(*) и (**)) на стр 16.), затем применим свойства неопределенного интеграла и табличные формулы
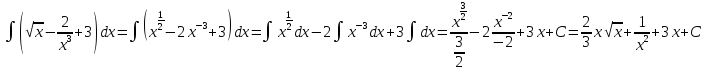
б) применяя свойства неопределённого интеграла и формулы (4), (6) таблицы интегралов, получим:
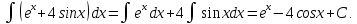
в)
Воспользуемся тем, что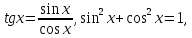 а
затем выполним деление под знаком
интеграла:
а
затем выполним деление под знаком
интеграла:
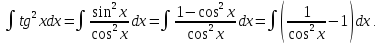
Записав полученный интеграл в виде разности двух интегралов, по формулам (8) и (1) таблицы получим:
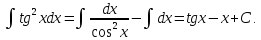
г) Раскрыв скобки и записав интеграл в виде разности интегралов, а затем применив формулы (5) и (9) таблицы, имеем:
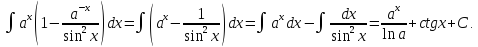
Все рассмотренные неопределенные интегралы найдены при помощи свойств неопределённого интеграла, простейших тождественных преобразований и основных табличных интегралов.
В более сложных случаях, когда этот способ не позволяет получить результат, иногда помогает переход к новой переменной (интегрирование подстановкой). В таких случаях целесообразнее пользоваться таблицей интегралов, в которой за аргумент принимается переменная u = u(x), являющаяся дифференцируемой функцией переменной x.
Приведём эту таблицу.
1а.
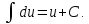
2a.
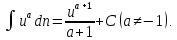
3a.
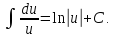
4a.
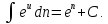
5a.
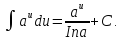
6a.
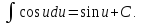
7a.
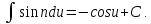
8a.
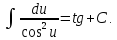
9a.
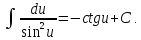
10a.
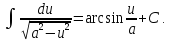
11a.
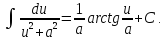
12a.
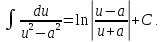
13a.
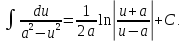
14a.
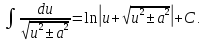
Задача 14. Найти:
а)
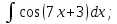 б)
б)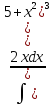
в)
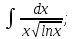 г)
г)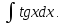
Решение.
а)
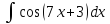
Если
ввести переменную z
= 7x+3
и найти дифференциалы обеих частей
равенства 7х+3 = z,
то получим 7dx
= dz,
откуда
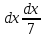 и
поэтому
и
поэтому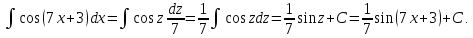
Здесь применили формулу (6а) и затем перешли к прежнему аргументу, заменив z = 7x+3.
б)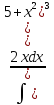
Сделав
подстановку z
= 5+x2.
Найдём dz
= 2xdxи
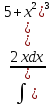 оттуда
применив формулу (2а) и перейдя к прежнему
аргументу, имеем
оттуда
применив формулу (2а) и перейдя к прежнему
аргументу, имеем
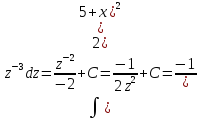
То
есть
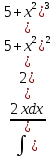
в)
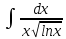
Здесь
удобно заменить lnx
= z
и, найдя
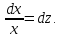 подставить в подынтегральное выражение:
подставить в подынтегральное выражение:
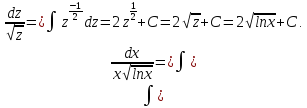
г)
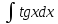
В
этом случае целесообразно заменить
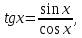 а затем, введя новую переменнуюz
= cosx,
найти dz
= - sinxdx.
Поставив под знак интеграла sinxdx=
-dz
и cosx
= z,
получем результат:
а затем, введя новую переменнуюz
= cosx,
найти dz
= - sinxdx.
Поставив под знак интеграла sinxdx=
-dz
и cosx
= z,
получем результат:
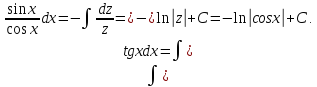
Тема 7. Определённый интеграл.
Основные вопросы теории:
Задачи приводящие к понятию определённого интеграла
Определённый интеграл как предел интегральных сумм. Основные свойства определённого интеграла
Формула Ньютона – Лейбница для вычисления определённого интеграла.
Приближённое вычисление определённого интеграла.
Понятие о несобственном интеграле с бесконечными пределами.
Простейшие приложения определенного интеграла
Примеры решения задач.
Для вычисления определённого интеграла служит формула Ньютона - Лейбница:
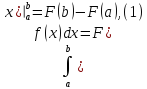
где
F(x)–
первообразная функции
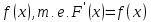
Задача 15
Найти площадь фигуры, ограниченной параболой y = 3x2 – 6xи прямой y = 3x.
Решение.
Площадь Sфигуры, ограниченной сверху непрерывной кривой y=f(x),снизу – непрерывной кривой y=g(x), вычисляется по формуле:
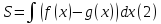
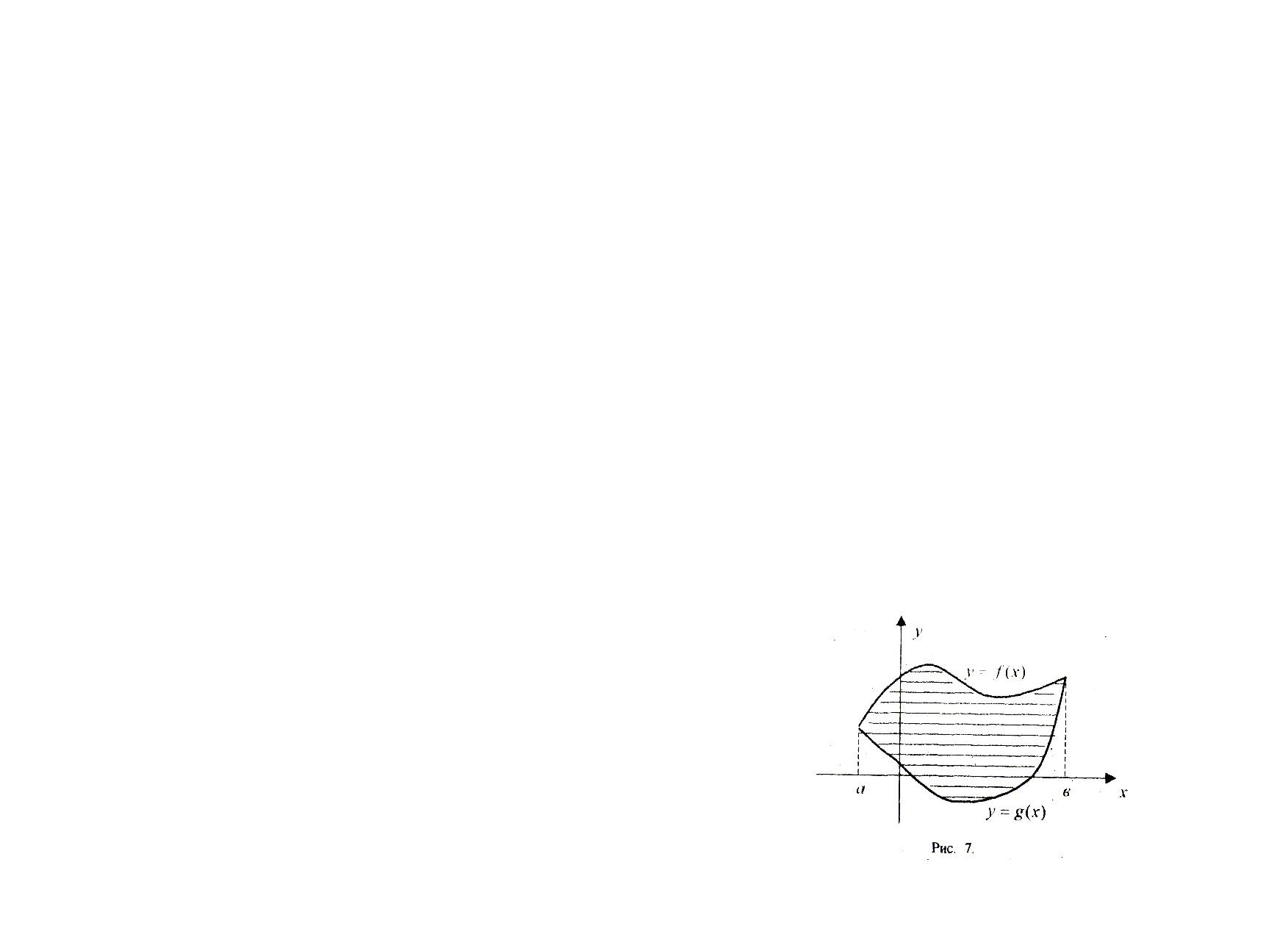
Найдём
точки пересечения указанные в задаче
15 линий, решив систему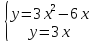
Тогда3x-3x2+6x=0, 9x-3x2=0, 3x∙(3-x)=0, откуда x=0, y=0 или х=3, у=9.
Следовательно, линии пересекаются в точках: О(0,0), А(3,9). Парабола у=3х2-6х пересекает ось ОХ в точках, где у=0, т.е. 3х2-6х=0, 3х∙(х-2)=0, х=0 или х=2. Поэтому порабола пересекает ось ОХ в точках О(0,0) и В(2,0). Вершина параболы Симеет координаты х=1, у(1)=3∙12-6∙1=-3, т.е. С(1,-3).
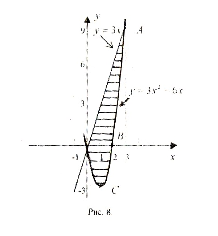
Здесь f(x)=3x, g(x)=3x2-6x, a=0, b=3, поэтому воспользовавшись формулами (2) и (1), получим: