Тема 5. Применение производной к исследованию функций.

Основные вопросы теории.

1. Теоремы о возрастании и убывании функции.

2. Экстремум функции. Необходимое условие существование экстремума дифференцируемой функции. Достаточные условия существования экстремума.

3. Нахождение наибольшего и наименьшего значений непрерывной функции на заданном отрезке.

4. Выпуклость и вогнутость кривой. Точки перегиба графика функции. Дифференциальные признаки выпуклости, вогнутости кривой и точки перегиба

5. Общая схема исследования функций и построения их графиков.

Примеры решения задач.

Задача 8. Найти интервалы возрастания и убывания функции:

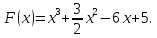
Решение:

Известно, что функция возрастает на тех интервалах, на которых ее первая производная положительна, и убывает там, где ее первая производная отрицательна. Границами интервалов возрастания и убывания функции являются точки экстремума. Из необходимого условия существования экстремума следует, что у дифференцируемой функции точки экстремума являются стационарными(критическими), т.е. в точках экстремума

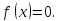
Найдем стационарные точки заданной функции 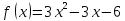обращается в нуль.

Когда

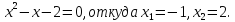
На числовой оси отложим найденные значения 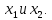На полученных интервалах определим знак производной:

Таким образом, функция f(x) возрастает при

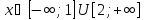
и f(x) убывает при

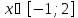
Задача 9.

Исследовать на экстремум функцию задачи 8.

Решение

Дифференцируемая функция имеет в критической точке экстремум, если 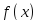меняет знак при переходе через точку В данном случае при переходе через критические точки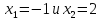

Первая производная меняет знак, поэтому в этих точках есть экстемумы. При переходе через точку 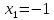производная меняет знак с плюса на минус, следовательно, в этой точке функция имеет максимум:

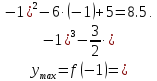
При переходе через точку 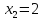первая производная меняет знак с минуса на плюс, следовательно, в этой точке функция имеет минимум:

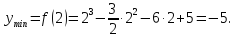
Задача 10.

Найти интервалы вогнутости и выпуклости перегиба графика функции

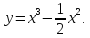
Решение:

Известно, что если вторая производная 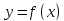функцииy = f(x) положительна (отрицательна) на некотором промежутке, то график такой функции на этом промежутке вогнутый (выпуклый). График функции имеет при 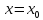точку перегиба, если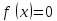и вторая производная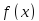меняет свой знак при переходе через эту точку.

Найдем 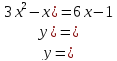и приравняем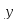к нулю: 6x-1=0 при

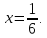
Исследуем знак 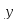слева и справа от точки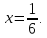

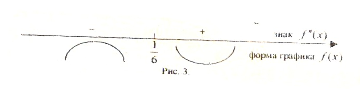
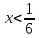
При 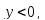следовательно график функции выпуклый на интервале []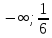

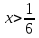
При 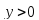, поэтому график функции вогнутый на интервале [].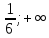

В точке 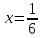вторая производная обращается в нуль и меняет свой знак при переходе через нее, поэтому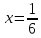график имеет точку перегиба. Ордината точки перегиба

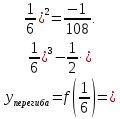
Итак, точка перегиба

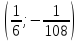
Задача 11.

Провести полное исследование функции

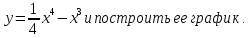
Решение.

1. Данная функция является многочленом, поэтому определена и непрерывна на всей действительной оси, т.е. при

2. 

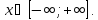
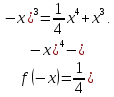
Так как не выполняются ни равенства f(-x) = f( x) (что явилось бы признаком четной функции), ни f(-x) = -f(x) ( что свидетельствовало бы о нечетности функции), то данная функция общего вида.

3. При 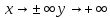, т.е. точки графика с возрастанием |х| удаляются наверх.

4. Точки пересечения графика с осью ОХ найдем, приравняв y к нулю:

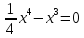
или 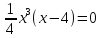, отсюда х = 0 или х = 4, т.е. график функции пересекает ось ОХ в точках О(0;0) и А(4;0)

Находя точки пересечения графика с осью OY и подставляя для этого в формулу функциональной зависимости значение х = 0, получаем ту же точку О(0;0).

5. Найдем промежутки возрастания и убывания (монотонного изменения) функции и точки экстремума.

Первая производная функции

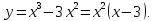
Критические точки найдем из условия 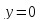(необходимого условия экстремума дифференцируемой функции):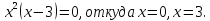

Эти точки разделили действительную ось на три промежутка: [], [], [].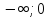

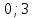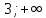Исследуя знак 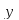на каждом промежутке, убеждаемся, что при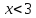первая производная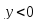и, следовательно, функция убывает, а при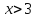первая производная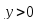, т.е. функция возрастает.

Результаты исследования схематически изображены на рис.4.

В критической точке x=3 – производная 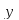меняет свой знак с минуса на плюс, следовательно,x = 3 – точка минимума.

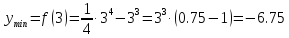
Итак, получена еще одна точка графика функции: B(3;-6.75).

6. Исследуем теперь формулу графика и найдем точки перегиба. Для этого найдем вторую производную функции 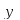и, приравняв её к нулю, вычислим корни получившегося уравнения:

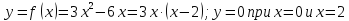
Точки х=0 и х=2 разбивают числовую ось на три промежутка[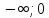],[0;2],[2;+]

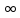Исследуя знак 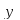на каждом промежутке, видим, что:

При 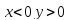и график функции вогнутый;

При 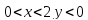и график функции выпуклый;

При 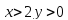и график функции вогнутый;

Схематически результаты исследования изображены на рис.5: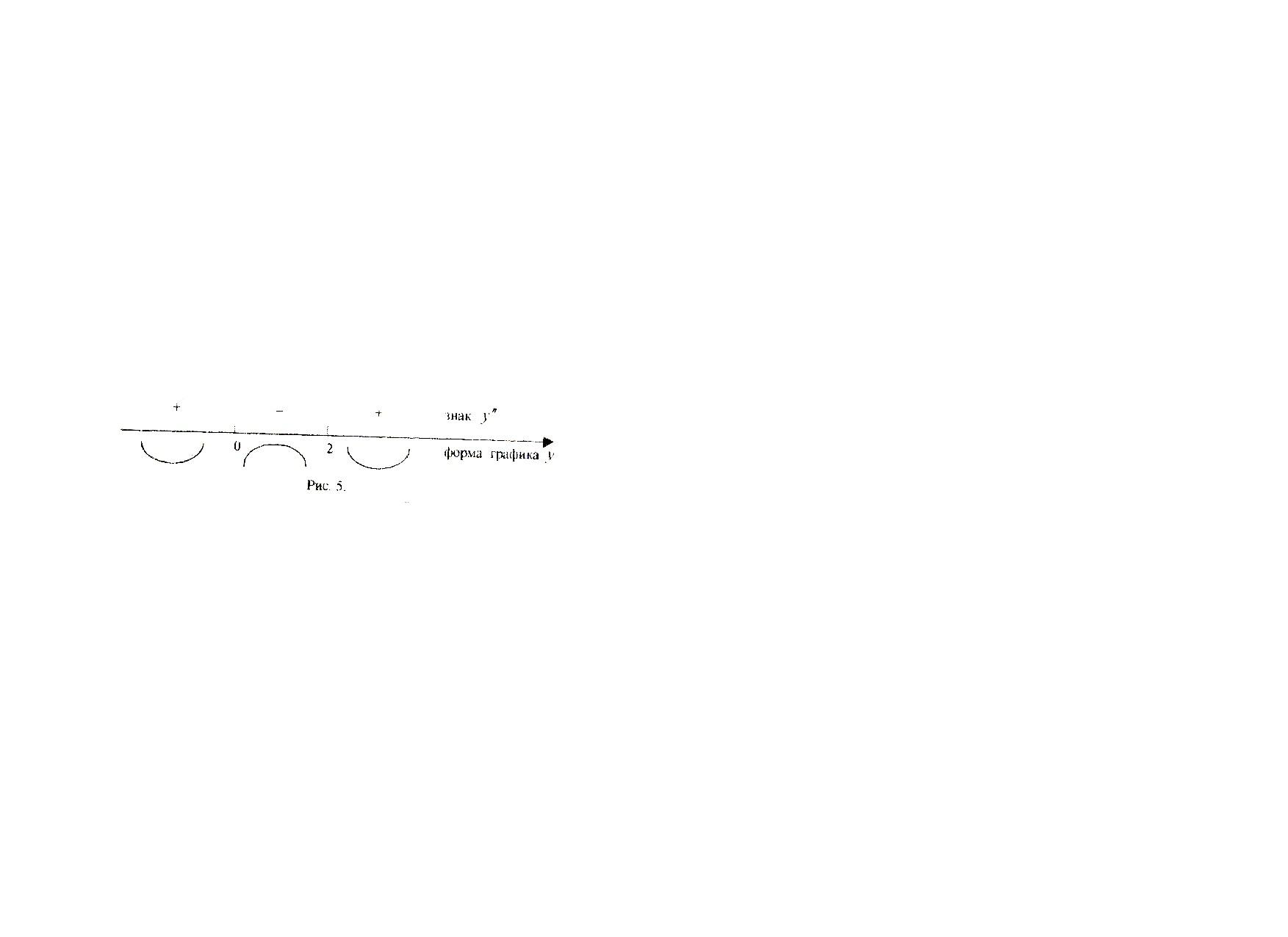

В точках х=0 и х=2 есть перегиб, так как в них вторая производная равна нулю (т.е. выполняется необходимое условие существования точки перегиба) и 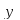меняет знак при переходе через эти точки (выполнено и достаточное условие существования точки перегиба).

Вычислим ординаты точек перегиба:

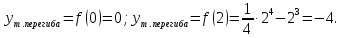
Итак, О(0;0) и С(2;4) – точки перегиба.

7. На основании всех полученных данных строим график функции. Для этого отмечаем на плоскости XOY найденные точки О, А,В и С. Можно найти координаты дополнительных точек. Найдем например,

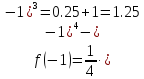
Итак, Д(-1;1.25) – дополнительная точка графика.

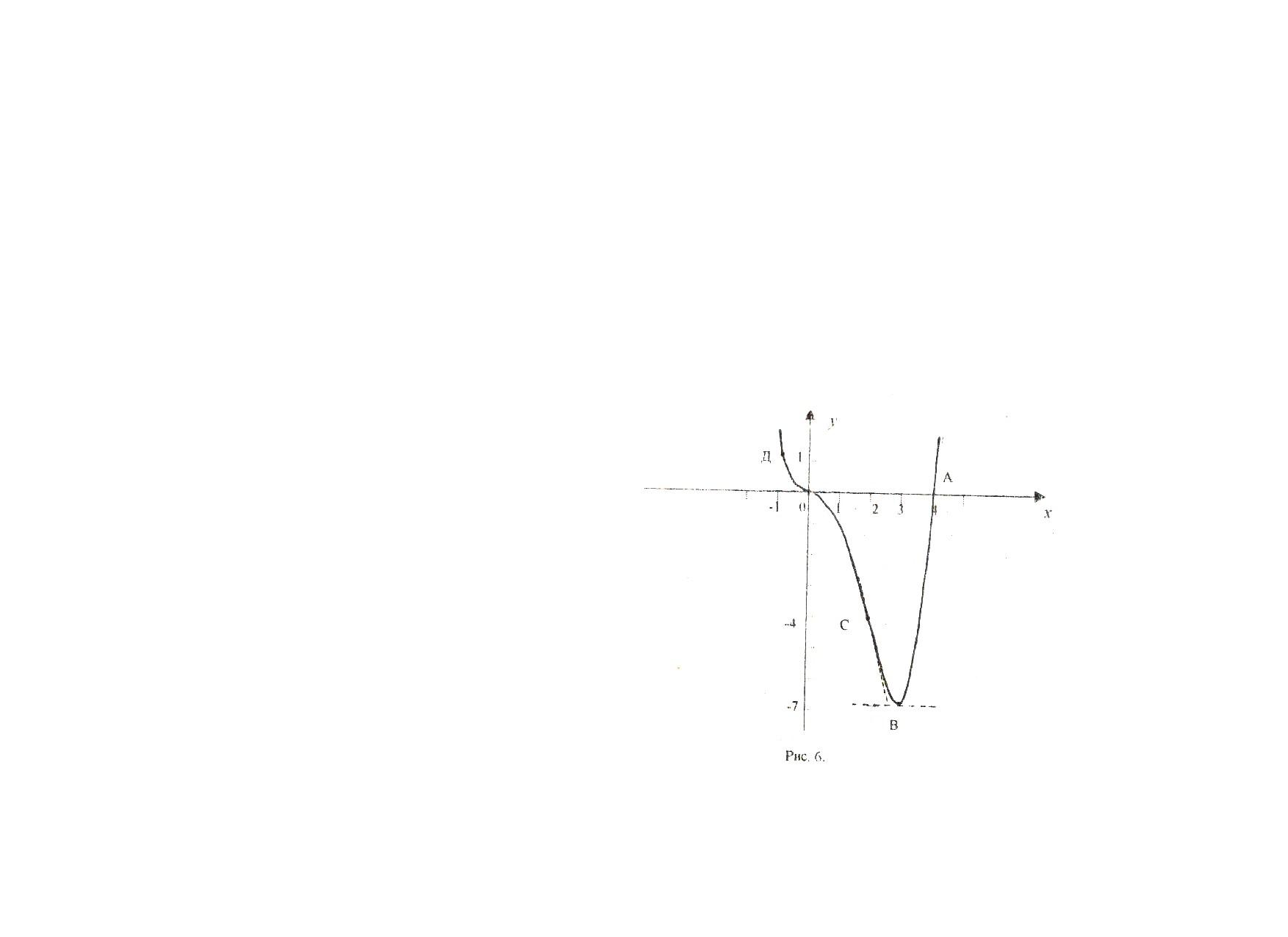
Замечание1. При построении графика функции нужно иметь ввиду, что на участках выпуклости график функции расположен под касательной, проведенной в любой точке, а на участках вогнутости, наоборот, - над касательной. В точках перегиба график переходит с одной стороны касательной на другую (см. рис.6, точки О и С).

В экстремальных точках касательная параллельна оси ОХ (см. рис6, точка В).

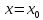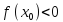Замечание2. Для нахождения точек экстремума можно пользоваться и вторым достаточным условием: если в критической точке вторая производная дифференцируемой функции отлична от нуля, то в этой точке есть экстремум. Это максимум, если , и минимум, если.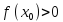

Например, в задаче 11, х=0, х=3 - критические точки.

Найдем в этих точках 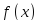;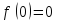, поэтому, требуется исследовать знак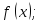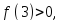следовательно, в точке х=3 функция имеет минимум.

Задача 12. Найти наименьшее и наибольшее значение функции 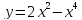на отрезке []

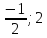Решение

Данная функция, являлась многочленом, непрерывна на заданном отрезке и, следовательно, достигает на нем своего наименьшего и наибольшего значений. Для того, чтобы их найти, поступим следующим образом.

1. Найдем критические точки, принадлежащие данному отрезку, и вычислим в них значения функции (не исследуя на экстремум):

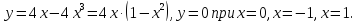
Данному отрезку принадлежат критические точки х =0 и х=1.

2. Вычислим значения функции на концах отрезка:

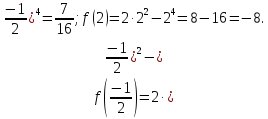
3. Сравнивая полученные результаты f(2)= - 8, f(0)=0, f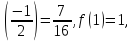выбираем из них наибольшее и наименьшее значения и получаем:

Наименьшее значение функции на данном отрезке –f(2)= -8,

наибольшее ее значение – f(1)=1.