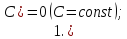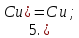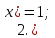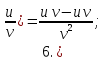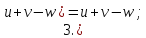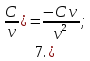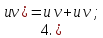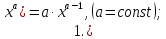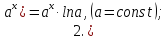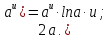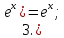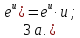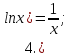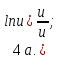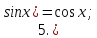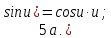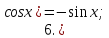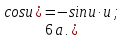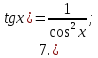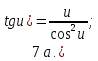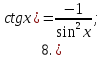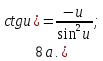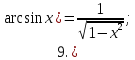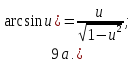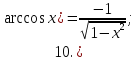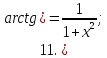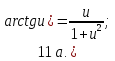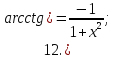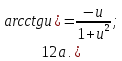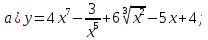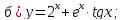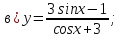Тема 3. Введение в математический анализ.

Основные вопросы теории:

1. Переменная величина и область ее изменения. Понятие функции. Область определения функции.

2. Основные элементарные функции, их свойства и графики.

3. Предел переменной величины. Предел функции. Основные теоремы о пределах.

4. Бесконечно малая величина. Теоремы о бесконечно малых величинах. Бесконечно большая величина.

5. Сравнение бесконечно малых величин.

6. Первый замечательный предел:

7. Второй замечательный предел: 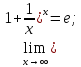число е; натуральный логарифм. Раскрытие простейших неопределителей.

8. Приращение аргумента и приращение функции.

9. Определение непрерывности функции в точке и на промежутке. Основные теоремы о непрерывных функциях. Точки разрыва функции.

Примеры решения задач.

Задача 5. Найти пределы указанных функций:

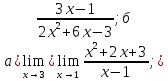
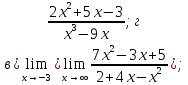
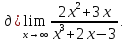
Решение:

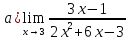
Данная дробно-рациональная функция при предельном значении аргумента х = 3 имеет знаменатель, отличный от нуля, и является непрерывной. Поэтому для нахождения ее предела при х → 3 достаточно аргумент х заменить его предельным значением, а именно:

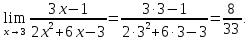
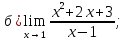
Числитель и знаменатель дроби – непрерывные функции и при х → 1 знаменатель есть величина бесконечно малая, а числитель имеет конечный предел, отличный от нуля. Итак, под знаком предела находится произведение функции х² + 2х +3, имеющей конечный предел, отличный от нуля, на функцию 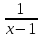, которая при х →1 является бесконечно большой величиной как величина, обратная бесконечно малой величине. Поэтому данная функция является бесконечно большой. Условно это обозначается символом ∞.

Следовательно,

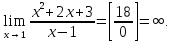
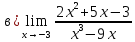
если непосредственно в данную функцию подставить вместо х его предельное значение

-3, то получим выражение вида 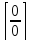– неопределённость. В подобных случаях числитель и знаменатель необходимо разложить на множители, сократить дробь и затем перейти к пределу.

В числители находится квадратный трёхчлен вида ах² + вх + с, корни которого находим по формуле: 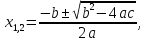а именно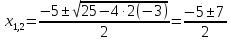, т.е.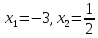

Так как

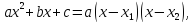
то

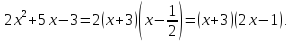
Знаменатель разложим на множители, вынося общий множитель х за скобки и применив формулу разности квадратов

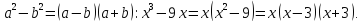
Итак, .

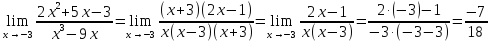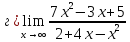
Теорему о пределе частного здесь применять нельзя, так как и числитель и знаменатель конечного предела не имеют. В этом случае говорят, что имеет место неопределённость вида 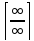. В подобных примерах для раскрытия такой неопределённости можно разделить числитель и знаменатель на степень х с наивысшим показателем, а затем перейти к пределу. Деля числитель и знаменатель дроби на х² и используя теоремы о пределах и свойства бесконечно малых величин получаем:

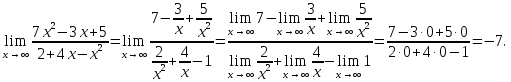
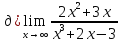
При х→∞ числитель и знаменатель дроби являются бесконечно большими величинами, т.е. имеем неопределённость 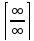. Разделив числитель и знаменатель дроби на х³, перейдём к пределу при х →∞:

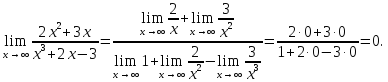
Тема 4. Производная и дифференциал функции.

Основные вопросы теории:

1. Задачи, приводящие к понятию производной. Определение производной. Геометрический смысл производной.

2. Правила дифференцирования. Производная суммы и произведения нескольких функций. Дифференцирование сложной функции.

3. Формулы дифференцирования основных элементарных функций.

4. Понятие о дифференциале функции. Применение дифференциала для приближенного вычисления значений функции.

5. Производная второго порядка.

Для справки приводим основные правила дифференцирования:

Если y=f(u), а u=u(x), то y=f(u(x)) – сложная функция от х. Производная сложной функции равна произведению этой функции по промежуточному аргументу u на производную промежуточного аргумента u по независимой переменной x:

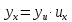
Запишем теперь таблицу производных основных элементарных функций, давая рядом формулы для сложной функции.

Примеры решения задач.

Задача 6.

Найти производные следующих функций:

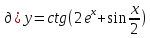
Решение

А) Введем дробные и отрицательные показатели степени, вспомнив, что:

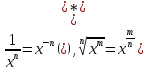
Получим

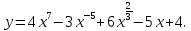
Применив правило дифференцирования аналитической суммы (3), правило вынесения постоянного множителя за знак производной (5), правило (1), а также формулу для производной степенной функции, получаем:

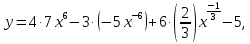откуда, используя формулы (*), (**), имеем:

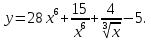
б) По правилу дифференцирования произведения (4) и табличные формулы получаем:

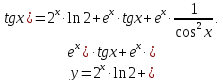
в) Применяем правила дифференцирования дроби (6), суммы (3) и табличные формулы:

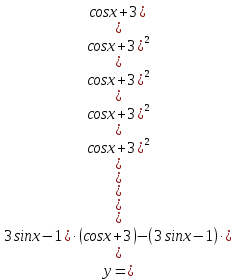
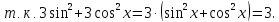
г) Применив (**), запишем функцию в виде степени 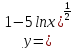, а затем применим формулу производной сложной функции:

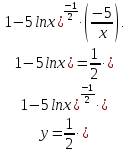
Ответ запишем, применив (*), (**):

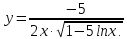
д) Применив формулу производной сложной функции и формулы таблицы производных, получаем:

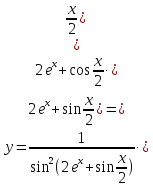
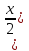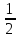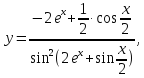Так как =, тооткуда умножив числитель и знаменатель на2, получаем ответ: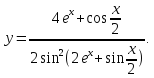

Задача 7.

Найти дифференциал функции:

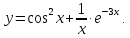
Решение

Запишем функцию иначе:

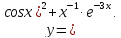
По определению, дифференциал dy функции y = f(x) вычисляется по формуле

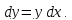
Поэтому сначала найдем производную данной функции, применив правила дифференцирования суммы (3) и произведения (4), формулу производной сложной функции и формулы таблицы производных:

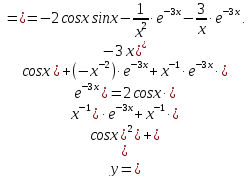
Заметив, что 2sinx cosx = sin2x и вынося их из последних двух слагаемых за скобку ,

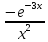Получаем :

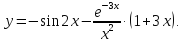
Найдем теперь дифференциал y: .
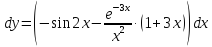