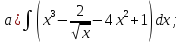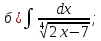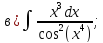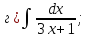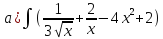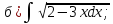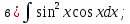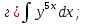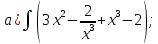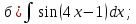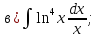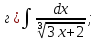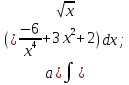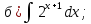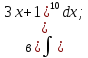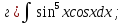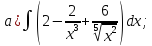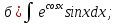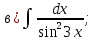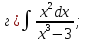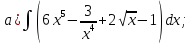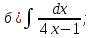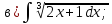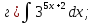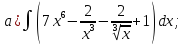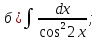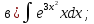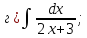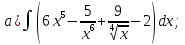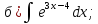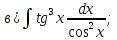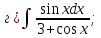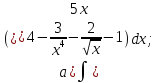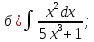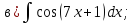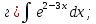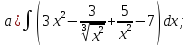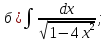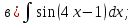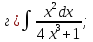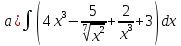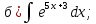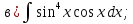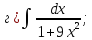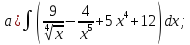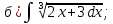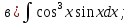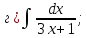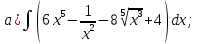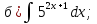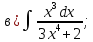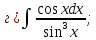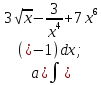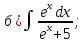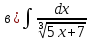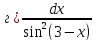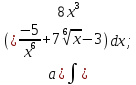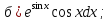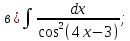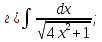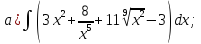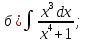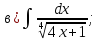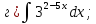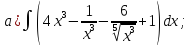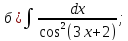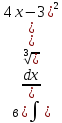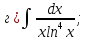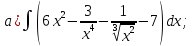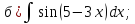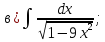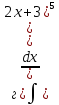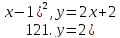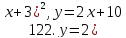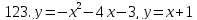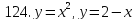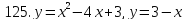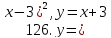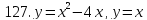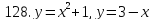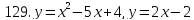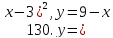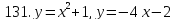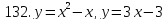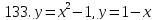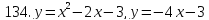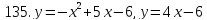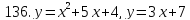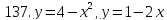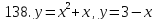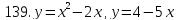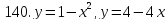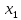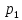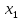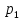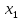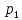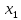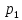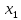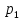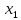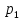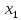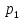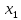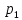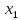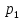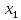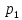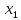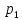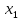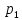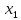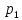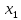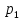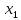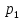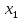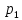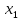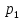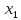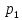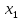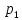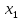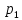- •Методические указания и контрольные работы
- •Тема 1. Определители и системы линейных алгебраических уравнений.
- •Тема 2. Элементы аналитической геометрии на плоскости.
- •Тема 3. Введение в математический анализ.
- •Тема 4. Производная и дифференциал функции.
- •Тема 5. Применение производной к исследованию функций.
- •Тема 6. Неопределенный интеграл.
- •Тема 7. Определённый интеграл.
- •Тема 8. Основные понятия теории вероятностей.
- •Тема 9. Теоремы о вероятности суммы и произведения событий.
- •Тема 10. Повторные испытания.
- •Тема 11. Случайные величины и их числовые характеристики.
- •Тема 12. Основные сведения из математической статистики.
- •Тема 13. Статистические оценки параметров распределения.
- •Тема 14. Корреляционная зависимость.
Тема 13. Статистические оценки параметров распределения.
Основные вопросы теории.
Выборочная средняя. Практические приёмы ее вычисления. Оценка генеральной средней по выборочной средней.
Выборочная дисперсия. Практические приёмы ее вычисления. Групповая, внутригрупповая, межгрупповая, межгрупповая и общая дисперсии. Оценка генеральной дисперсии по исправленной выборочной дисперсии.
Примеры решения задач.
Задача 27.
Плодовитость свиноматок крупной белой породы по второму опоросу составила: 11; 16; 14; 12; 8; 12; 14; 10; 11; 13; 11; 13; 10; 11; 14; 13; 12; 12; 12; 11; 12; 13; 12; 13; 10.
Определить:
Величину, которую следует принять за среднюю генеральной совокупности (выборочную среднюю);
Величину, которую следует принять за дисперсию генеральной совокупности (исправленную выборочную дисперсию);
Доверительный интервал для
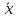 с вероятностью 0,9545.
с вероятностью 0,9545.
Решение.
В
качестве приближённого значения средней
генеральной совокупности
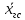 принимаем выборочную среднюю:
принимаем выборочную среднюю:
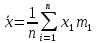
Для оценки дисперсии генеральной совокупности применим формулу:
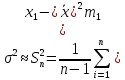
Среднее квадратическое отклонение выборочной средней находим по формуле:
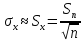
Перепишем результаты наблюдений в порядке возрастания вариант (ранжируем ряд): 8; 10; 10; 10; 11; 11; 11; 11; 11; 12; 12; 12; 12; 12; 12; 12; 13; 13; 13; 13; 13; 14; 14; 14; 16.
Определим частоты различных вариант:
|
xi |
8 |
10 |
11 |
12 |
13 |
14 |
16 |
|
mi |
1 |
3 |
5 |
7 |
5 |
3 |
1 |
Найдём выборочную среднюю
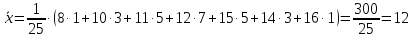
Итак,
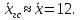
В качестве дисперсии генеральной совокупности принимаем исправленную выборочную дисперсию:
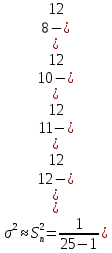
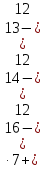
В курсе математической статистики доказано, что для вероятности 0,9545 в случае нормального распределения наблюдаемой случайной величины доверительный интервал имеет вид
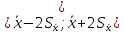 ,
гдеSx
(среднее квадратическое отклонение
выборочной средней) находим по формуле
,
гдеSx
(среднее квадратическое отклонение
выборочной средней) находим по формуле
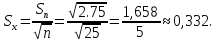
Следовательно,
доверительный интервал для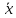 при заданной надежности 0,9545 получается
таким:
при заданной надежности 0,9545 получается
таким:
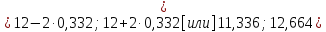
Тема 14. Корреляционная зависимость.
Основные вопросы теории.
Зависимость случайных величин
Метод наименьших квадратов
Коэффициент корреляции. Корреляционная таблица.
Линии регрессии.
Пример решения задачи.
Задача 28.
Даны результаты измерения двух случайных величин Х и У:
|
xi |
8 |
16 |
8 |
13 |
12 |
11 |
9 |
12 |
14 |
17 |
|
уi |
17 |
7 |
16 |
9 |
13 |
11 |
14 |
10 |
7 |
6 |
Вычислить коэффициент корреляции.
Решение.
Для вычисления коэффициента корреляции применим формулу:

Для
упорядочения записей все вспомогательные
вычисления оформим в виде таблицы 5. В
ней наблюдаемые значения х и у запишем
столбцами суммы для вычисления средних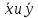 запишем внизу каждого столбца. Правее
расположим столбцы, в которых вычисляем
разности
запишем внизу каждого столбца. Правее
расположим столбцы, в которых вычисляем
разности
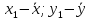 их
квадраты и их произведения. Нужные для
вычисления коэффициента корреляции
суммы
их
квадраты и их произведения. Нужные для
вычисления коэффициента корреляции
суммы
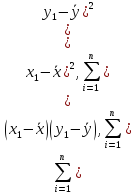 найдём путем суммирования значений,
записанных в соответствующих столбцах.
найдём путем суммирования значений,
записанных в соответствующих столбцах.
Таблица 5.
|
N |
X1 |
Y1 |
X1- |
(X1- |
X1- |
(X1- |
(X1- |
|
1 |
8 |
17 |
-4 |
16 |
6 |
36 |
-24 |
|
2 |
16 |
7 |
4 |
16 |
-4 |
16 |
-16 |
|
3 |
8 |
16 |
-4 |
16 |
5 |
25 |
-20 |
|
4 |
13 |
9 |
1 |
1 |
-2 |
4 |
-2 |
|
5 |
12 |
13 |
0 |
0 |
2 |
4 |
0 |
|
6 |
11 |
11 |
-1 |
1 |
0 |
0 |
0 |
|
7 |
9 |
14 |
-3 |
9 |
3 |
9 |
-9 |
|
8 |
12 |
10 |
0 |
0 |
-1 |
1 |
0 |
|
9 |
14 |
7 |
2 |
4 |
-4 |
16 |
-8 |
|
10 |
17 |
6 |
5 |
25 |
-5 |
25 |
-25 |
|
∑ |
120 |
110 |
|
88 |
|
136 |
-104 |
Средние
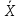 и
и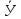 равны
равны
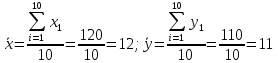
Из таблицы 5
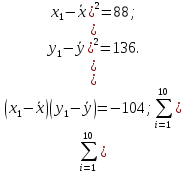
Подставляя найденные значения в формулу для коэффициента корреляции, получаем:
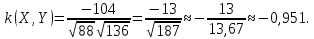
Итак, зависимость случайных величин Xи Y характеризуется отрицательным коэффициентом корреляции – 0,951.
ЗАДАЧИ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ.
1-20. Решить систему трех линейных алгебраических уравнений с тремя неизвестными по формулам Крамера.
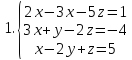
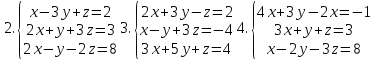
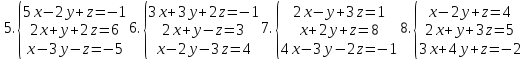
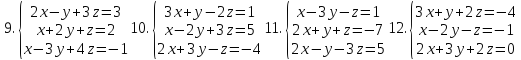
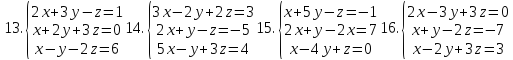
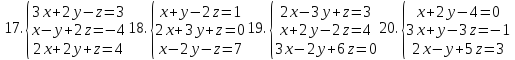
21-25. Даны координаты вершин треугольника АВС. Найти:
Уравнение стороны АВ.
Уравнение стороны CD, проведённой из вершины С на сторону АВ.
Уравнение прямой, проходящей через середину стороны АВ, параллельно АС.
Уравнение окружности, для которой сторона АВ является диаметром.
Сделать чертёж в прямоугольной системе координат.
21. А(-3;-1), B(9;3), C(4;8).
22. A(-2;3), B(10;7), C(5;12),
23. A(-1;-1), B(11;3), C(6;8)
24. A(-5;-3), B(7;1), C(2;6),
25 A(-3;5), B(9;9), C(4;14).
26-30. Даны координаты вершин треугольника АВС. Найти:
Уравнение стороны АВ.
Уравнение стороны CD, проведённой из вершины С на сторону АВ.
Уравнение медианы АЕ,
Уравнение окружности, для которой медиана АЕ является диаметром.
Сделать чертёж в прямоугольной системе координат.
26. А(-1;-1), B(2;8), C(12;2).
27.A(1;1), B(4;10), C(14;4),
28. A(-5;1), B(-2;10), C(8;4)
29. A(-2;-4), B(1;5), C(11;-1),
30.A(-6;1), B(-3;10), C(7;4).
31-35. Даны координаты вершин треугольника АВС. Найти:
Уравнение стороны ВС.
Уравнение высоты AD, проведённой из вершины A на сторону BC.
Уравнение прямой, проходящей через середину стороны BC, параллельно АB.
Уравнение окружности, для которой сторона BC является диаметром.
Сделать чертёж в прямоугольной системе координат.
31. А(0;1), B(3;10), C(13;4).
32. A(-5;-1), B(-2;8), C(8;2),
33. A(-1;-2), B(2;7), C(12;1)
34. A(-4;-4), B(-1;5), C(9;-1),
35A(-6;0), B(-3;9), C(7;3).
36-40. Даны координаты вершин треугольника АВС. Найти:
Уравнение стороны BC.
Уравнение стороны AD, проведённой из вершины A на сторону BC.
Уравнение медианы ВЕ,
Уравнение окружности, для которой сторона ВЕ является диаметром.
Сделать чертёж в прямоугольной системе координат.
36. А(4;13), B(1;4), C(14;7).
37.A(0;6), B(-3;-3), C(10;0),
38. A(-4;11), B(-7;2), C(6;5)
39. A(5;4), B(2;-5), C(15;-2),
40.A(-5;14), B(-8;5), C(5;8).
41-60. Найти пределы указанных функций:
|
41.
a)
|
б)
|
|
42.
a)
|
б)
|
|
43.
a)
|
б)
|
|
44.
a)
|
б)
|
|
45.
a)
|
б)
|
|
46.
a)
|
б)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
61-80. Пользуясь правилами дифференцирования, найти производные и дифференциалы следующих функций:
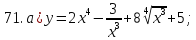
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
|
81-100. Провести полное исследование функции и построить её график.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
101-120. Найти определенные интегралы:
|
|
|
|
101. |
|
|
|
|
|
|
|
|
102. |
|
|
|
|
|
|
|
|
103. |
|
|
|
|
|
|
|
|
104. |
|
|
|
|
|
|
|
|
105. |
|
|
|
|
|
|
|
|
106. |
|
|
|
|
|
|
|
|
107. |
|
|
|
|
|
|
|
|
108. |
|
|
|
|
|
|
|
|
109. |
|
|
|
|
|
|
|
|
110. |
|
|
|
|
|
|
|
|
111. |
|
|
|
|
|
|
|
|
112. |
|
|
|
|
|
|
|
|
113. |
|
|
|
|
|
|
|
|
114. |
|
|
|
|
|
|
|
|
115. |
|
|
|
|
|
|
|
|
116. |
|
|
|
|
|
|
|
|
117. |
|
|
|
|
|
|
|
|
118. |
|
|
|
|
|
|
|
|
119. |
|
|
|
|
|
|
|
|
120. |
|
|
|
|
121-140. Даны уравнения параболы и прямой. Вычислить с помощью определенного интеграла площадь фигуры, ограниченной данными линиями; сделать чертеж и заштриховать искомую площадь.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
141. При выращивании рассады в промышленных теплицах сбой в системе освещения в лечение недели возможен с вероятностью0.02, в системе теплоснабжения - с вероятностью 0.01, в системе орошения - с вероятностью 0.05. Найти вероятность того, что в течение недели сбоев в работе теплицы не будет.
142. В распоряжении агрохимика имеется 6 различных видов минеральных удобрений (А,В,C,D,E,F). Ему необходимо провести несколько экспериментов по изучению совместного влияния любой тройки минеральных удобрений. Найти вероятность того, что в выбранной наугад тройке удобрений не окажется удобрения А.
143. Имеется два одинаковых на вид ящика картофеля, В первом – 70% картофеля сорта Луговской, а во втором - 50%. Из каждого ящика взяли по одному клубню. Найти вероятность того, что оба клубня будут сорта Луговской.
144. В хозяйстве из 30 автомашин 6 машин - полуторатонки. 15 имеют грузоподъемность в 2т и 9 - в Зт. Две случайно оказавшиеся свободными машины были посланы за грузом.Его оказалось 5т, Какова вероятность того, что посланные машины сумели его полностью забрать.
145. При выращивании рассады в промышленных теплицах сбои в системе освещения в течение недели возможен с вероятностью 0,03, в системе теплоснабжения с вероятностью 0,02, в системе орошения с вероятностью0.07. Найти вероятность тою, что в течение недели будут сбои в работе теплицы.
146. При проведении фитопрочисток на сортосеменном участке вероятности обнаружить растения с заболеваниями А, В и С равны 0.05. 0,03 и 0.01 соответственно. Какова вероятность обнаружить больное ""растение на данном участке?
147. В букете 5 синих, 6 красных и 4 белых астры. Из букета наудачу выбраны три цветка Найти вероятность того, что все они будут не белые.
148. В условиях сырой и холодной погоды вероятности развития у растений картофеля заболеваний А, В или С равны соответственно 0.2. 0.1 к 0.4 Найти вероятность того, что наугад выбранный куст картофеля не будет больным.
149. В одном из отсеков овощехранилища находятся 15 контейнеров с капустой сорта Надежда и 25-с капустой сорта Подарок. В наугад выбранном контейнере оказалась капуста сорта Подарок. Найти вероятность того, что в следующем наугад выбранном контейнере окажется капуста того же сорта.
150. Вероятность того, что в данной местности температура воздуха в любой день июля опустится ниже 5°С, равна 0.01, Найти вероятность того, что в течение первых трех дней июля температура будет не меньше 5°С.
151. На садовый участок для посадки было привезено 6 саженцев красной смородины, 3 белой и 8 черной. Из всех саженцев наугад взяли один. Он оказался саженцем черной смородины. Какова вероятность того, что следующий наугад взятый саженец будет саженцем белой смородины?
152.Имеется 5 семян редкого растения со всхожестью 60%. Семена высеваются по очереди (каждое следующее высевается только в том случае, когда предыдущее не взошло ).Определить вероятность того, что понадобится высеять пятое семя.
153.В эксперименте с уничтожением некоторого сельскохозяйственного вредителя - насекомого обнаружено, что при первом применении средства погибают 80% насекомых. Среди оставшихся в живых насекомых процент погибающих при каждом повторном применении средства уменьшается в 2 раза. Найти вероятность того, что насекомое останется в живых после трех применений средства.
154. Известно, что если организм существует в течение 20минут, то он расщепляется на 2 новых организма (происходит деление). На протяжении 20 минут каждый организм погибает с вероятностью 0.3. Предполагается, что случаи выживания отдельных организмов независимы. Найти вероятность того, что к концу часа будет в живых 8 организмов, если опыт начался с одного организма.
155.Вероятность повреждения рассады при понижении температуры ниже -2° С равна 0.1. При каждом следующем заморозке эта вероятность увеличивается на 0.1. Найти вероятность того, что растение после трех заморозков не пострадает.
156. Имеется два одинаковых, на вид ящика картофеля. В первом ящике - 70% клубней сорта Синеглазка и 30% - сорта Елизавета, а во втором - 40% клубней сорта Синеглазка и 60% - сорта Елизавета. Из каждого ящика взяли по одному клубню. Найти вероятность того, что клубни будут разных сортов.
157. При нарушении режима полива вероятность заболевания растения томата сорта А равна 0.02. сорта В - 0.015, сорта С - 0.01. В теплице произошел сбой в работе системы полива. Было выбрано по одному растению каждого сорта. Найти вероятность того, что
среди этих растений окажется не более одного больного.
158. Имеется два одинаковых на вид ящика, в каждом из которых лежат яблоки двух сортов. В первом ящике 40% яблок сорта А и 60% сорта В. а во втором - 70% сорта А и 30% сорта В. Из каждого ящика берут по одному яблоку. Найти вероятность того, что яблоки
будут одного сорта.
159. Было приобретено по одному черенку трех редких видов растений. Известно, что черенки первого растения укореняются с вероятностью 0,3, второго - с вероятностью 0.1, третьего - с вероятностью 0,15. Найти вероятность того, что из купленных черенков укоренятся не менее двух.
160. Для высадки рассады в пленочной теплице были направлены три пары работниц, Каждая пара выполняет свою часть задания, которое будет выполнено при условии выполнения всех частей. Вероятность выполнения своей части задания в установленный срок работницами первой пары равна 0,8, второй - 0,75, третьей 0,9. Найти вероятность того, что задание будет полностью выполнено в установленный срок.
161. Всхожесть семян равна 80%. Для опыта отбирается 5 семян. Определить вероятность того, что будет не менее четырех всходов.
162. Доля плодов, зараженных болезнью в скрытой форме, составляет 25%. Случайным образом отбирают 6 плодов. Определили вероятность того, что среди них окажется:
1)3зараженных плода, 2) не более одного зараженного плода.
163. Вероятность зараженности зерна вредителями в скрытой форме составляет 0.002. Определить вероятность того, что в выборке из -500 зерен окажется ровно 3 зараженных.
164. Вероятность того, что расход воды в течение дня не превысит норму, равна 0,75. Найти вероятность того, что расход воды будет нормальным в течение четырех из пяти ближайших дней.
165. Вероятность выживания бактерий после радиоактивного облучения равна 0,004. Найти вероятность того, что после облучения из 500 бактерий останутся выжившими не более 3 бактерий.
166. В семенах содержится 0,1% семян сорняков. Какова вероятность при случайном отборе 2000 семян обнаружить 5 семян сорняков.
167. В хлопке число длинных волокон составляет 80%. Каковы вероятности того, что во взятом наудачу пучке из 5 волокон длинных окажется: 1) три: 2) не более двух.
168. При закладке фруктового сада было посажено 400 деревьев. Вероятность того, что дерево приживется, равна 0.8.Найти вероятность того, что прижившихся деревьев
будет 325.
169. Всхожесть семян данного растения равна 0.9. Найти вероятность того, что из 900 посеянных семян взойдет не менее 795, но не более 820.
170. Вероятность повреждения при транспортировке рассады белокочанной капусты
равна 0.1. Найти вероятность того, что из 10 наугад взятых растений будет повреждено не более одного.
171. Вероятность того, что семя подсолнечника окажется невосприимчивым к болезни, равна 0,001. Найти вероятность того, что из 1000 посеянных семян вырастет одно растение, невосприимчивое к болезни.
172. Вероятность того, что используемая в теплице лампа перегорит в течение недели, равна 0.002. Найти вероятность того, что в теплице за неделю из 500 ламп перегорит не более двух.
173. Вероятность повреждения яблони при сильных морозах равна 0.3. Найти вероятность того, что из 100 яблонь будет повреждено не менее 25, но не более 40.
174. Появление колонии микроорганизмов данного вида в определенных условиях оценивается вероятностью 0.8. Какова вероятность того, что при проведении 4 опытов эта колония появится не менее трех раз?
175.Вероятность установления в данной местности устойчивого снежного покрова с
1 ноября равна 0,1. Определить вероятность того, что в ближайшие три года устойчивый снежный покров установится, по крайней мере, один раз.
176. Вероятность того, что из взятого случайным образом зерна вырастет колос, содержащий не менее 50 зерен, равна 0,6. Вычислить вероятность того, что из взятых наудачу трех зерен не вырастет ни одного колоса, содержащего не менее 50 зерен.
177. 65% выращенных в хозяйстве арбузов имеют вес более 3 кг. Найти вероятность того, что из 5000 закупленных в хозяйстве арбузов будет не менее 3200 арбузов весом более 3 кг.
178. Вероятность дождливого дня летом в засушливой местности равна 0.01. Найти вероятность того, что летом в этой местности будет два дождливых дня.
179. В некоторой области в течение года град приносит значительный ущерб хозяйству с вероятностью 0.02. Определить вероятность того, что из 200 хозяйств, имеющихся в области, пострадает не более двух хозяйств.
180. Вероятность гибели насекомого-вредителя под действием некоторого средства равна 0.8. Найти вероятность того, что под действием этого средства из 100 насекомых погибнет не менее 75.
181-200. Задан закон распределения вероятностей дискретной случайной величины в виде таблицы: в первой строке таблицы указаны возможные значения случайной величины, во второй -соответствующие вероятности. Вычислить:
математическое ожидание;
дисперсию:
среднее квадратическое отклонение.
Начертить многоугольник распределения и показать на нем вычисленное математическое ожидание.
|
181. |
|
-5 |
4 |
6 |
9 |
|
|
0.2 |
0.1 |
0.3 |
0.4 |
|
182. |
|
-1 |
1 |
3 |
5 |
6 |
|
|
0.2 |
0.3 |
0.3 |
0.1 |
0.1 |
|
183. |
|
2 |
5 |
10 |
12 |
|
|
|
0.1 |
0.3 |
0.4 |
0.2 |
|
|
184. |
|
-3 |
0 |
1 |
2 |
5 |
|
|
0.1 |
0.2 |
0.4 |
0.2 |
0.1 |
|
185. |
|
-2 |
1 |
4 |
6 |
|
|
|
0.2 |
0.3 |
0.1 |
0.4 |
|
|
186. |
|
-4 |
-1 |
0 |
2 |
3 |
|
|
0.2 |
0.1 |
0.3 |
0.3 |
0.1 |
|
187. |
|
1 |
3 |
5 |
8 |
|
|
|
0.2 |
0.3 |
0.1 |
0.4 |
|
|
188. |
|
-2 |
-1 |
3 |
4 |
6 |
|
|
0.1 |
0.3 |
0.4 |
0.1 |
0.1 |
|
189. |
|
-3 |
-1 |
2 |
5 |
|
|
|
0.3 |
0.2 |
0.4 |
0.1 |
|
|
190. |
|
-1 |
0 |
1 |
4 |
5 |
|
|
0.3 |
0.3 |
0.2 |
0.1 |
0.1 |
|
191. |
|
0.1 |
0.3 |
0.5 |
1 |
|
|
|
0.2 |
0.5 |
0.2 |
0.1 |
|
|
192. |
|
-4 |
0 |
4 |
8 |
12 |
|
|
0.1 |
0.3 |
0.4 |
0.1 |
0.1 |
|
193. |
|
3 |
4 |
6 |
7 |
|
|
|
0.3 |
0.2 |
0.4 |
0.1 |
|
|
194. |
|
-3 |
-1 |
0 |
2 |
5 |
|
|
0.1 |
0.2 |
0.3 |
0.3 |
0.1 |
|
195. |
|
-1 |
0 |
3 |
9 |
|
|
|
0.1 |
0.2 |
0.4 |
0.3 |
|
|
196. |
|
-6 |
-1 |
4 |
9 |
14 |
|
|
0.1 |
0.2 |
0.2 |
0.4 |
0.1 |
|
197. |
|
2 |
7 |
9 |
10 |
|
|
|
0.3 |
0.2 |
0.1 |
0.4 |
|
|
198. |
|
-2 |
0 |
1 |
4 |
7 |
|
|
0.1 |
0.4 |
0.2 |
0.2 |
0.1 |
|
199. |
|
1 |
2 |
4 |
7 |
|
|
|
0.2 |
0.4 |
0.3 |
0.1 |
|
|
200. |
|
1 |
2 |
3 |
4 |
5 |
|
|
0.1 |
0.2 |
0.4 |
0.2 |
0.1
|
201 – 205.Случайные значения веса плодов в одном ящике распределены нормально. Средний вес плодов в одном ящике равен α кг, а среднее квадратическое отклонение в весе плодов в одном ящике рано σ кг. Определить:
вероятность того, что вес плодов в одном ящике окажется не менее α кг;
наибольшее значение, которое не превысит вес плодов в ящике с вероятность. 0,95.
201. α = 10, σ = 0,5, α = 9,4.
202. α = 15, σ = 0,8, α = 14,5.
203. α = 8, σ = 0,2, α = 7,7.
204. α = 12, σ = 0,3, α = 11,5.
205. α = 10, σ = 0,4, α = 9,5.
206 – 210. Средняя глубина посева семян составляет αсм; отдельные отклонения от этого значения случайные, распределены нормально со средним квадратическим отклонением
σ см. Определить:
долю семян, посеянных на глубину более αсм;
долю семян, посеянных на глубину менее ß см.
206. α = 5,σ = 0,6, α = 5,5, ß= 4.
207. α = 6, σ = 0,4, α = 6,5, ß = 5.
208. α = 5,5, σ = 0,5, α = 6, ß = 4,5.
209. α = 5, σ = 0,4,α = 6, ß = 5,5.
210. α = 7,σ = 0,8, α = 8,5 , ß = 5.
211 – 215. Случайные значения веса зерна распределены нормально. Среднее значение веса зерна равно α г, среднее квадратическое отклонение равно σ г. Нормальные всходы дают зерна, вес которых болееα г. Определить:
процент семян, которые дадут нормальные всходы;
величину которую не превзойдет вес отдельного зерна с вероятностью 0,98.
|
|
|
211. α = 0,17,σ = 0,04, α = 0,12.
212. α = 0,15,σ = 0,03, α = 0,10.
213. α = 0,18,σ = 0,05, α = 0,15.
214. α = 0,16,σ = 0,03, α = 0,10.
215. α = 0,20,σ = 0,5, α = 0,17.
216 – 220. Размер плода - случайная величина, распределенная нормально. Средний , размер плода равен αсм, среднее квадратическое отклонение равно σ см. Определить:
1)процент плодов, имеющих размер более αсм;
2)величину, которую не превысит размер плода свероятностью 0,99.
216. α = 6,σ = 1,2, α = 5.
217. α = 7,5,σ = 1,5, α = 5,5.
218. α = 8,σ = 1,3, α = 6,5.
219. α = 6,5,σ = 1,1, α = 5,5.
220. α = 7,σ = 1,2, α = 5,5.
221 – 230 В таблице 6 даны результаты обследования выборки, где наблюдалась дискретная случайная величина. Составить вариационный ряд, построить многоугольник относительных частот.
Таблица 6.
|
Номер наблюдения |
Данные для задач | |||||||||
|
221 |
222 |
223 |
224 |
225 |
226 |
227 |
228 |
229 |
230 | |
|
1 |
2 |
4 |
0 |
1 |
3 |
1 |
2 |
4 |
3 |
5 |
|
2 |
3 |
9 |
2 |
7 |
6 |
1 |
6 |
5 |
2 |
8 |
|
3 |
1 |
2 |
2 |
3 |
2 |
2 |
3 |
2 |
1 |
2 |
|
4 |
3 |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
4 |
3 |
|
5 |
3 |
6 |
4 |
6 |
6 |
3 |
5 |
5 |
2 |
5 |
|
6 |
3 |
2 |
6 |
4 |
4 |
6 |
4 |
4 |
3 |
2 |
|
7 |
2 |
6 |
2 |
1 |
4 |
3 |
2 |
5 |
3 |
7 |
|
8 |
1 |
1 |
5 |
2 |
3 |
5 |
2 |
3 |
1 |
1 |
|
9 |
3 |
5 |
2 |
5 |
7 |
1 |
4 |
6 |
2 |
4 |
|
10 |
1 |
7 |
9 |
2 |
6 |
8 |
1 |
5 |
0 |
6 |
|
11 |
2 |
3 |
2 |
3 |
4 |
2 |
3 |
4 |
2 |
3 |
|
12 |
2 |
9 |
6 |
4 |
6 |
5 |
3 |
5 |
1 |
8 |
|
13 |
2 |
4 |
5 |
2 |
2 |
5 |
2 |
2 |
2 |
4 |
|
14 |
2 |
4 |
1 |
4 |
3 |
2 |
5 |
4 |
3 |
5 |
|
15 |
4 |
6 |
2 |
7 |
4 |
2 |
7 |
4 |
4 |
6 |
|
16 |
4 |
4 |
9 |
5 |
6 |
8 |
4 |
5 |
3 |
3 |
|
17 |
0 |
4 |
3 |
3 |
6 |
3 |
3 |
6 |
0 |
4 |
|
18 |
1 |
6 |
0 |
1 |
3 |
1 |
2 |
4 |
2 |
7 |
|
19 |
1 |
4 |
1 |
4 |
3 |
1 |
4 |
3 |
1 |
4 |
|
20 |
2 |
8 |
0 |
2 |
3 |
1 |
3 |
4 |
3 |
9 |
231 – 240.
В таблице 7 даны результаты обследования выборки, где наблюдалась непрерывная случайная величина. Составить интервальный ряд распределения, разбив диапазон значений случайной величины на 5 интервалов и построить гистограмму относительных частот.
241 – 260.
По результатам обследования выборки определить:
величину, которую следует принять за среднюю генеральной совокупности;
величину которую следует принять за дисперсию генеральной совокупности;
доверительный интервал, границы которого удалены от выборочной средней на два средних квадратических отклонения.
Данные взять из таблиц 8 или 9.
Таблица 7.
|
Номер наблюдения |
Данные для задач | |||||||||
|
231 |
232 |
233 |
234 |
235 |
236 |
237 |
238 |
239 |
240 | |
|
1 |
39.1 |
6.9 |
8.0 |
1.8 |
11.6 |
44.1 |
7.0 |
11.9 |
16.0 |
0.8 |
|
2 |
27.6 |
14.5 |
2.7 |
3.8 |
18.9 |
24.8 |
3.7 |
10.0 |
13.9 |
5.8 |
|
3 |
24.8 |
16.6 |
1.2 |
2.0 |
11.8 |
22.6 |
1.2 |
11.6 |
11.8 |
2.0 |
|
4 |
24.4 |
9.8 |
2.0 |
2.8 |
8.1 |
29.4 |
1.0 |
14.4 |
13.1 |
1.8 |
|
5 |
35.8 |
4.5 |
6.1 |
1.2 |
9.5 |
40.8 |
7.0 |
9.5 |
14.5 |
2.2 |
|
6 |
26.1 |
15.8 |
2.0 |
4.3 |
12.7 |
21.1 |
1.0 |
10.8 |
7.7 |
3.3 |
|
7 |
26.6 |
11.7 |
2.7 |
3.2 |
10.1 |
32.4 |
0.4 |
10.4 |
6.6 |
2.7 |
|
8 |
17.4 |
5.4 |
1.4 |
3.7 |
1.6 |
26.6 |
2.7 |
11.7 |
10.1 |
3.2 |
|
9 |
33.1 |
11.5 |
9.8 |
1.9 |
14.3 |
25.7 |
8.0 |
12.2 |
14.5 |
2.9 |
|
10 |
20.7 |
7.2 |
7.0 |
1.9 |
9.5 |
33.1 |
9.8 |
11.5 |
14.3 |
1.9 |
|
11 |
37.1 |
10.5 |
3.3 |
2.1 |
10.2 |
31.4 |
4.5 |
9.4 |
11.7 |
1.7 |
|
12 |
36.1 |
13.4 |
4.5 |
3.7 |
16.7 |
37.1 |
4.3 |
10.5 |
10.2 |
3.1 |
|
13 |
37.4 |
15.1 |
4.8 |
1.8 |
16.4 |
32.4 |
5.8 |
10.5 |
11.4 |
2.8 |
|
14 |
38.2 |
15.2 |
6.1 |
1.4 |
10.5 |
45.5 |
1.6 |
10.3 |
11.0 |
2.2 |
|
15 |
39.5 |
12.3 |
2.6 |
3.2 |
6.0 |
38.2 |
7.1 |
11.2 |
10.5 |
2.4 |
|
16 |
42.8 |
11.1 |
6.3 |
4.6 |
12.4 |
39.3 |
2.2 |
13.4 |
13.7 |
3.1 |
|
17 |
44.3 |
18.4 |
2.6 |
3.1 |
18.7 |
42.8 |
6.3 |
11.1 |
12.4 |
3.6 |
|
18 |
23.8 |
6.0 |
3.4 |
0.3 |
6.6 |
28.8 |
3.4 |
11.0 |
11.6 |
2.3 |
|
19 |
25.5 |
15.4 |
1.7 |
2.7 |
15.2 |
20.5 |
0.7 |
10.4 |
10.2 |
3.7 |
|
20 |
35.3 |
19.2 |
9.4 |
2.6 |
14.7 |
30.3 |
10.4 |
14.0 |
9.7 |
2.6 |
Таблица 8.
|
Номер наблюдения |
Данные для задач | |||||||||
|
241 |
242 |
243 |
244 |
245 |
246 |
247 |
248 |
249 |
250 | |
|
1 |
4 |
4 |
11 |
13 |
6 |
17 |
5 |
10 |
11 |
11 |
|
2 |
5 |
5 |
13 |
8 |
6 |
10 |
2 |
12 |
7 |
10 |
|
3 |
5 |
6 |
13 |
10 |
2 |
12 |
6 |
9 |
8 |
5 |
|
4 |
4 |
3 |
14 |
10 |
9 |
13 |
4 |
11 |
10 |
4 |
|
5 |
2 |
5 |
15 |
11 |
4 |
13 |
4 |
13 |
13 |
7 |
|
6 |
3 |
4 |
15 |
12 |
9 |
12 |
4 |
11 |
13 |
7 |
|
7 |
4 |
4 |
10 |
10 |
5 |
15 |
5 |
10 |
11 |
8 |
|
8 |
6 |
5 |
12 |
14 |
6 |
16 |
5 |
9 |
7 |
7 |
|
9 |
4 |
4 |
11 |
14 |
7 |
13 |
3 |
5 |
13 |
9 |
|
10 |
5 |
6 |
16 |
9 |
7 |
15 |
3 |
9 |
14 |
7 |
|
11 |
2 |
5 |
10 |
14 |
7 |
11 |
4 |
8 |
13 |
12 |
|
12 |
5 |
5 |
15 |
8 |
3 |
9 |
4 |
6 |
11 |
11 |
|
13 |
3 |
7 |
16 |
11 |
8 |
13 |
5 |
9 |
12 |
8 |
|
14 |
3 |
5 |
13 |
16 |
5 |
13 |
5 |
7 |
11 |
4 |
|
15 |
3 |
6 |
15 |
13 |
7 |
15 |
3 |
11 |
10 |
9 |
|
16 |
4 |
4 |
14 |
13 |
5 |
11 |
2 |
7 |
6 |
12 |
|
17 |
4 |
5 |
14 |
15 |
7 |
8 |
3 |
11 |
9 |
9 |
|
18 |
3 |
4 |
14 |
12 |
11 |
15 |
5 |
12 |
8 |
10 |
|
19 |
6 |
5 |
17 |
16 |
5 |
10 |
4 |
7 |
14 |
4 |
|
20 |
4 |
4 |
16 |
12 |
9 |
13 |
4 |
10 |
11 |
8 |
|
21 |
5 |
5 |
18 |
9 |
5 |
13 |
2 |
10 |
9 |
10 |
|
22 |
5 |
6 |
12 |
15 |
7 |
12 |
3 |
10 |
11 |
9 |
|
23 |
3 |
3 |
12 |
11 |
7 |
11 |
4 |
14 |
11 |
8 |
|
24 |
4 |
6 |
16 |
12 |
8 |
10 |
6 |
8 |
12 |
8 |
|
25 |
4 |
5 |
18 |
12 |
9 |
8 |
6 |
6 |
9 |
6 |
Таблица 9.
|
Номер наблюдения |
Данные для задач | |||||||||
|
251 |
252 |
253 |
254 |
255 |
256 |
257 |
258 |
259 |
260 | |
|
1 |
6 |
8 |
7 |
10 |
2 |
12 |
10 |
8 |
12 |
18 |
|
2 |
4 |
5 |
6 |
12 |
4 |
11 |
8 |
10 |
8 |
16 |
|
3 |
4 |
8 |
7 |
4 |
6 |
8 |
7 |
13 |
11 |
12 |
|
4 |
7 |
7 |
9 |
4 |
4 |
11 |
9 |
13 |
9 |
13 |
|
5 |
5 |
5 |
5 |
8 |
5 |
8 |
12 |
13 |
11 |
18 |
|
6 |
7 |
8 |
8 |
4 |
4 |
11 |
13 |
10 |
13 |
15 |
|
7 |
4 |
3 |
7 |
8 |
6 |
10 |
11 |
10 |
10 |
17 |
|
8 |
6 |
9 |
5 |
7 |
5 |
9 |
6 |
15 |
15 |
14 |
|
9 |
5 |
8 |
7 |
9 |
2 |
5 |
13 |
13 |
14 |
13 |
|
10 |
3 |
6 |
8 |
8 |
3 |
9 |
14 |
16 |
9 |
14 |
|
11 |
5 |
7 |
7 |
12 |
4 |
7 |
13 |
10 |
15 |
14 |
|
12 |
7 |
4 |
8 |
10 |
5 |
6 |
8 |
9 |
8 |
12 |
|
13 |
6 |
6 |
9 |
8 |
5 |
9 |
13 |
8 |
10 |
16 |
|
14 |
7 |
7 |
4 |
5 |
4 |
8 |
11 |
13 |
16 |
16 |
|
15 |
5 |
3 |
6 |
9 |
3 |
11 |
8 |
11 |
12 |
10 |
|
16 |
2 |
5 |
5 |
11 |
2 |
7 |
7 |
11 |
13 |
15 |
|
17 |
3 |
5 |
7 |
9 |
3 |
10 |
9 |
8 |
14 |
11 |
|
18 |
5 |
7 |
11 |
11 |
4 |
12 |
8 |
8 |
12 |
11 |
|
19 |
6 |
4 |
5 |
4 |
4 |
6 |
14 |
9 |
16 |
10 |
|
20 |
3 |
5 |
9 |
7 |
5 |
10 |
6 |
12 |
12 |
15 |
|
21 |
7 |
8 |
5 |
10 |
2 |
11 |
10 |
13 |
10 |
16 |
|
22 |
6 |
7 |
7 |
9 |
3 |
10 |
9 |
12 |
14 |
15 |
|
23 |
5 |
6 |
6 |
8 |
4 |
9 |
11 |
11 |
11 |
13 |
|
24 |
4 |
5 |
9 |
7 |
5 |
8 |
12 |
10 |
12 |
14 |
|
25 |
3 |
4 |
8 |
6 |
6 |
7 |
8 |
9 |
13 |
12 |
261 – 280. Вычислить коэффициент корреляции двух случайных величин X иY.
Данные взять из таблиц 10, 11 или 12.
Таблица 10.
|
Номер наблюдения |
Данные для задач | |||||||
|
261 x y |
262 x y |
263 x y |
264 x y |
265 x y |
266 x y |
267 x y |
268 x y | |
|
1 |
2 8 |
5 11 |
6 20 |
6 20 |
11 18 |
10 4 |
8 5 |
8 7 |
|
2 |
5 7 |
9 8 |
9 9 |
9 10 |
20 2 |
16 18 |
12 12 |
14 13 |
|
3 |
10 5 |
11 6 |
5 14 |
11 6 |
11 20 |
15 16 |
10 8 |
15 15 |
|
4 |
4 9 |
14 4 |
7 11 |
7 16 |
19 6 |
18 21 |
15 15 |
9 7 |
|
5 |
14 4 |
8 9 |
12 6 |
7 17 |
12 17 |
11 5 |
13 13 |
12 11 |
|
6 |
8 7 |
1 15 |
13 3 |
12 5 |
18 9 |
13 12 |
12 11 |
13 12 |
|
7 |
11 6 |
7 10 |
10 8 |
13 5 |
14 15 |
12 8 |
11 10 |
16 15 |
|
8 |
9 6 |
10 7 |
6 13 |
12 6 |
14 12 |
17 21 |
9 6 |
12 12 |
|
9 |
12 5 |
12 5 |
6 11 |
8 13 |
16 9 |
14 13 |
16 17 |
11 10 |
|
10 |
13 3 |
13 5 |
8 10 |
15 2 |
15 12 |
14 12 |
14 13 |
10 8 |
Таблица 11.
|
Номер наблюдения |
Данные для задач | |||||||
|
269 x y |
270 x y |
271 x y |
272 x y |
273 x y |
274 x y |
275 x y |
276 x y | |
|
1 |
9 3 |
12 8 |
61 57 |
35 25 |
3 5 |
8 6 |
18 20 |
8 26 |
|
2 |
16 14 |
8 2 |
60 58 |
20 18 |
4 6 |
10 8 |
19 20 |
7 26 |
|
3 |
18 18 |
15 11 |
59 54 |
20 19 |
5 8 |
11 9 |
20 20 |
11 36 |
|
4 |
10 5 |
15 12 |
58 55 |
20 20 |
6 7 |
4 3 |
21 25 |
15 46 |
|
5 |
11 6 |
18 15 |
56 52 |
30 25 |
7 11 |
10 9 |
23 25 |
19 50 |
|
6 |
17 16 |
13 9 |
57 56 |
25 21 |
9 10 |
11 7 |
22 25 |
23 60 |
|
7 |
20 21 |
14 10 |
59 60 |
25 23 |
3 4 |
7 6 |
23 30 |
27 66 |
|
8 |
14 10 |
17 14 |
56 56 |
25 22 |
9 11 |
5 8 |
24 30 |
31 70 |
|
9 |
12 8 |
19 16 |
58 56 |
30 23 |
6 8 |
6 4 |
25 30 |
35 75 |
|
10 |
13 8 |
9 13 |
56 56 |
30 24 |
8 10 |
5 3 |
25 35 |
34 66 |
Таблица 12.
|
Номер наблюдения |
Данные для задач |
| ||||
|
277 x y |
278 x y |
279 x y |
280 x y |
| ||
|
1 |
58 60 |
4 45 |
41 47 |
25 42 | ||
|
2 |
57 61 |
7 30 |
40 48 |
25 36 | ||
|
3 |
57 56 |
8 30 |
39 44 |
30 38 | ||
|
4 |
54 59 |
5 40 |
38 45 |
30 36 | ||
|
5 |
55 58 |
6 40 |
36 42 |
35 24 | ||
|
6 |
52 56 |
6 35 |
37 45 |
35 28 | ||
|
7 |
55 57 |
7 35 |
39 50 |
40 24 | ||
|
8 |
60 59 |
9 25 |
36 46 |
40 20 | ||
|
9 |
56 56 |
3 50 |
38 46 |
45 22 | ||
|
10 |
56 58 |
5 40 |
36 47 |
45 20 | ||
Приложение.
Таблица 1.
Значения
функции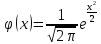
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9
2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9
3.0 3.1 3.2 3.3 3.4 3.5 |
0.3989 3970 3910 3814 3683 3521 3332 3123 2897 2661
2420 2179 1942 1714 1497 1295 1109 0940 0790 0656
0540 0440 0355 0283 0224 0175 0136 0104 0079 0060
0044 0033 0024 0017 0012 0009 |
3989 3965 3902 3802 3668 3503 3312 3101 2874 2637
2396 3155 1919 1691 1476 1276 1092 0925 0775 0644
0529 0431 0347 0277 0219 0171 0131 0101 0077 0058
0043 0032 0023 0017 0012 0008 |
3989 3961 3894 3790 3653 3485 3292 3079 2850 2613
2371 2131 1895 1669 1456 1257 1074 0909 0761 0632
0519 0422 0339 0270 0213 0167 0129 0099 0075 0056
0042 0031 0022 0016 0012 0008 |
3988 3956 3885 3778 3637 3467 3271 3056 2827 2589
2347 2107 1872 1647 1435 1238 1057 0893 0748 0620
0508 0413 0332 0264 0208 0163 0126 0096 0073 0055
0040 0030 0022 0016 0011 0008 |
3986 3951 3876 3765 3621 3448 3251 3034 2803 2565
2323 2083 1849 1626 1415 1219 1040 0878 0734 0608
0498 0404 0325 0258 0203 0158 0122 0093 0071 0053
0039 0029 0021 0015 0011 0008 |
3984 3945 3867 3752 3605 3429 3230 3011 2780 2541
2299 2059 1826 1604 1394 1200 1023 0863 0721 0596
0488 0396 0317 0252 0198 0154 0119 0091 0069 0051
0038 0028 0020 0015 0010 0007 |
3982 3939 3857 3739 3589 3410 3209 2989 2756 2516
2275 2036 1804 1582 1374 1182 1006 0848 0707 0584
0478 0387 0310 0246 0194 0151 0116 0088 0067 0050
0037 0027 0020 0014 0010 0007 |
3980 3932 3847 3726 3572 3391 3187 2966 2732 2492
2251 2012 1781 1561 1354 1163 1989 0833 0694 0573
0468 0379 0303 0241 0189 0147 0112 0086 0065 0048
0036 0026 0019 0014 0010 0007 |
3977 3925 3836 3712 3555 3372 3166 2943 2709 2489
2227 1989 1758 1539 1334 1145 0973 0818 0681 0562
0459 0371 0297 0235 0184 0143 0110 0084 0063 0047
0035 0025 0018 0013 0009 0007 |
3973 3918 3825 3697 3538 3352 3144 2920 2685 2444
2203 1965 1736 1518 1315 1127 0957 0804 0669 0551
0449 0363 0290 0229 0180 0139 0107 0081 0061 0046
0034 0025 0018 0013 0009 0006 |
Таблица 2.
Значение
функции
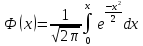
|
x |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9
2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9 |
0.000 0398 0793 1179 1554 1915 2258 2580 2881 3160
3413 3643 3849 4032 4192 4332 4452 4554 4641 4713
4773 4821 4861 4893 4918 4938 4953 4965 4974 4981
|
0040 0438 0832 1217 1591 1950 2291 2612 2910 3186
3438 3665 3869 4049 4207 4345 4463 4564 4649 4719
4778 4826 4865 4896 4920 4940 4955 4966 4975 4982 |
0080 0478 0871 1255 1628 1985 2324 2642 2939 3212
3461 3686 3888 4066 4222 4357 4474 4573 4656 4726
4783 4830 0 4868 4898 4922 4941 4956 4967 4976 4983
|
0120 0517 0910 1293 1664 2019 2357 2673 2967 3238
3485 3708 3907 4082 4236 4370 4485 4582 4664 4732
4788 4831 4871 4901 4925 4943 4957 4968 4977 4983 |
0160 0557 0948 1331 1700 2054 2389 2704 3000 3264
3508 3729 3925 4099 4251 4382 4495 4591 4671 4738
4793 4838 4875 4904 4927 4945 4959 4969 4977 4984 |
0199 0596 0987 1368 1736 2088 2422 2734 3023 3289
3531 3749 3944 4115 4265 4394 4505 4599 4678 4744
4797 4842 4878 4906 4929 4946 4960 4970 4978 4984 |
0239 0636 1026 1406 1772 2127 2454 2764 3051 3315
3554 3770 3962 4131 4279 4403 4515 4608 4686 4750
4803 4846 4881 4909 4931 4948 4961 4971 4979 4985 |
0279 0675 1064 1443 1808 2157 2486 2794 3079 3340
3575 3790 3980 4147 4292 4418 4525 4616 4693 4756
4808 4850 4884 4911 4932 4949 4962 4972 4980 4985 |
0919 0714 1103 1480 1844 2190 2518 2823 3106 3365
3599 3810 3997 4162 4306 4430 4535 4625 4700 4762
4812 4854 4887 4913 4934 4951 4963 4973 4980 4986 |
0359 0754 1141 1517 1879 2224 2549 2852 3133 3389
3621 3830 4015 4177 4319 4441 4545 4633 4706 4767
4817 4857 4890 4916 4936 4952 4964 4974 4981 4886 |
|
3.0 3.5 4.0 4.5 5.0 |
0.49865 49977 499968 499997 499999997 |
3.1 3.6
|
4990 4998 |
3.2 3.7 |
4.93 4999 |
3.3 3.8 |
4996 4999 |
3.4 3.9
|
4997 4999 5 | |

 )2
)2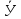
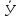 )2
)2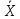 )
(X1-
)
(X1-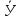 )
)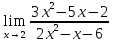
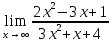
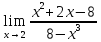
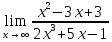
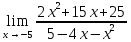
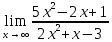
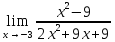
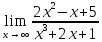
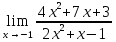
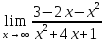
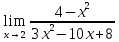
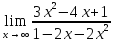
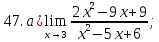
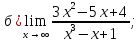
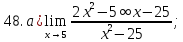
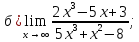
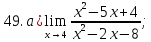
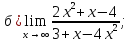
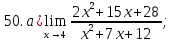
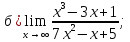
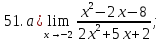
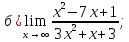
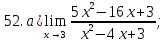
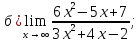
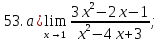
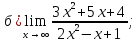
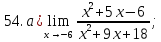
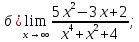
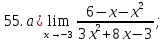
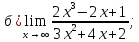
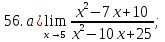
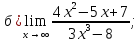
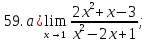
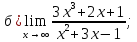
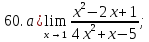
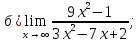
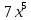 -
-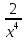 +6
+6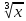 -3;
-3;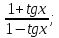
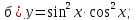
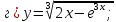
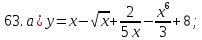
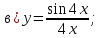
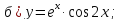
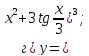
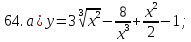
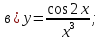
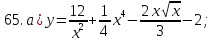
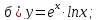
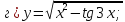
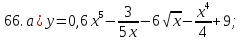
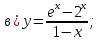
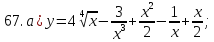
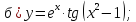
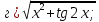
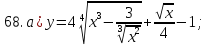
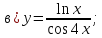
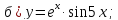
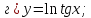
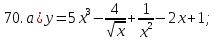
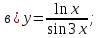
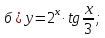
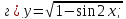
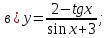
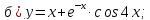
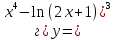
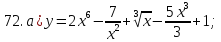
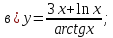
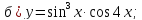
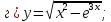
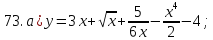
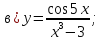
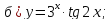
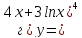
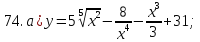
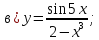
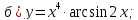
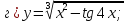
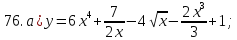
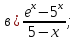
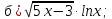
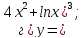
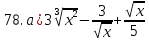
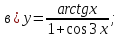
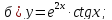
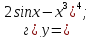
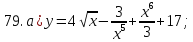
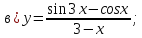
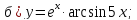
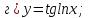
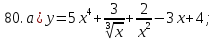
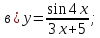
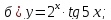
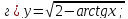
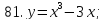
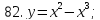
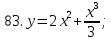
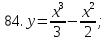
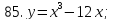
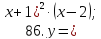
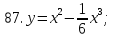
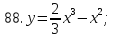
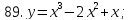
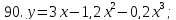
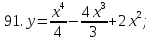
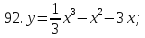
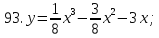
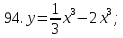
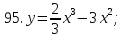
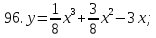
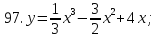
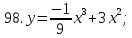
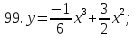
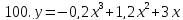 ;
;