Задание №3. Оптимизация дискретных управлений дискретными динамическими объектами методом динамического программирования р. Беллмана

Дано:

(1) k=0,1,2,3

(2)

, (3) n=4

U – н.у. (неограниченное управление), (4)

, (5)

Найти: (6).

Решение

1.

Минимизируем

Вычислим S₃ от x₃:

2.

Минимизируем

Вычислим S₂ от U₂:

3.

Минимизируем

Вычислим S₁ от U₂:

4.

Минимизируем

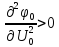
Вычислим S₀ от U₀:

Рассчитаем оптимальный процесс:

Рассчитаем оптимальное программное управление:

Задание №4. Синтез непрерывного оптимального управления с помощью уравнения Эйлера

Дано:

Найти: .

1. Выразим входное управляющее воздействие

Приведем задачу к варианту задачи на безусловный экстремум:

2.

3. Решим задачу с помощью уравнения Эйлера:

4. Решим ДУ Эйлера методом характеристического уравнения

p₁=-0,6, p₂=0,6

5. Т.к. x→∞, то

Учитывая, что x₀=C₁

Найдем оптимальную программу управления:

6. Найдем оптимальный регулятор (оптимальный закон управления):

7. Закон управления можно получить и другим способом:

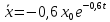
8.

9. Структурная схема:

Задание №5. Синтез непрерывных оптимальных уравнений с помощью уравнения Эйлера-Пуассона

Найти: .

1. Преобразуем эту задачу в вариационную задачу на безусловный экстремум:

2.

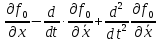
3.

+

4.

5.

6. Составим оптимальную синтезированную систему управления:

7. Структурная схема: