Метод фазовой плоскости

Метод распространяется на системы 2-ого порядка (это недостаток), все характеристики можем получить.

Основан на фазовых траекториях, которые строятся по плоскости по двум каким-то координатам.(рис.1)

Получим фазовую траекторию процесса: рис.2

Для периодического процесса постоянную амплитуду и частоту получили фазовую траекторию. То есть, в результате построений получили замкнутую кривую, то кривая с периодом и постоянной амплитудой.

В данном случае (рис 2) - это эллипс с

Х = а sinwt

Y = aw coswt

Гармонические колебания. рис.1 То есть, получили спираль. Для гармонических затухающих кривых - фазовая траектория - скручивающаяся спираль к "0".

Расходящиеся гармонические колебания. "Раскручивающаяся" спираль. Система в этом случае - не устойчива. ( рис.2)

Сходящиеся процессы. рис.1

То есть, для всех апериодических затухающих процессов фазовые траектории стягиваются к "0".

Апериодические расходящиеся процессы. рис.2

То есть, для расходящихся процессов - "уходят в бесконечность". Таким образом, если построим фазовую траекторию, то можем судить об автоколебаниях устойчивости.

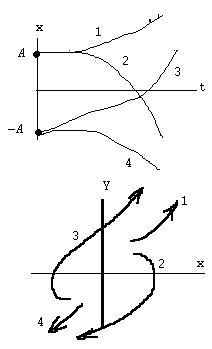
Автоколебания нелинейных систем

В нелинейных системах может быть автоколебание - когда выходная величина изменяется с постоянной амплитудой и частотой, наличие автоколебаний - не означает, что система не устойчива. Система может быть устойчивой и иметь автоколебания.

Использование системы зависит от того, для чего используется система.

Признак автоколебаний - замкнутая траектория фазовых характеристик на фазовых плоскостях. Это замкнутая траектория - предельный цикл.

В зависимости от начальных условий таких предельных циклов может быть несколько. Если в системе автоколебание - свидетельствует устойчивый предельный цикл.

Предельный цикл устойчивый, если все фазовые траектории как внутри так и снаружи стремятся к этому предельному циклу. Если фазовые траектории расходятся от этого цикла - не устойчивые.

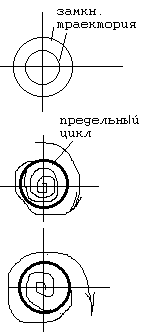
Имея устойчивый предельный цикл, можем определить параметры автоколебаний.

Амплитуда "а" примерно = ОА, a*w = OB; -> w= OB/OA;

Чтобы построить фазовую траекторию (НС 2-ого порядка):

dy dx

--- = Q(x,y); --- = P(x,y);

dy dy

Q(x,y) и P(x,y) - нелинейные ф-ии от входной величины и скорости этой величины. Надо исключить t. Получим:

dy Q(x,y)

---- = ----- ;

dt P(x,y)

Разобьем переменные, проинтегрируем обе части, получим уравнение, позволяющее построить фазовую траекторию.

Учитывая, что P(x,y) и Q(x,Y) часто прибегают к линейному приближению, разлагая в ряд Тейлора в окрестности точки (Хо,Уо)

dy dx

--- = ax+by; --- = cx +dy;

dt dt

dQ(x,y)

где a=------- в точке (Хо,Уо)

dx

dQ dP dP

b=---; c=---; d=---в точке (Хо,Уо)

dy dx dx;

Если все траектории стремятся к "0", то система устойчива. Используя приближенное представление:

y'=ax+by

x'=bx+dy

Можем перейти к одному уравнению. Характеристическое уравнение :

p^2 + kp + m =0;

По корням данного ХУ можно судить об устойчивости рассматриваемой системы:

1. незатухающий процесс: свойственен чисто мнимые корни ХУ (не затухают и не возрастают)

2. Затухающие процессы: комплексные корни с "-" вещественной частью

3. Расходящиеся процессы: комплексные корни с "+" вещесвенной частью

4. Апериодические затухающие процессы: вещественные "-" корни

5. Расходящиеся апериодические процессы: вещественные "+" корни