24

ПРОЕКТИРОВАНИЕ ПОЛУЗАКАЗНЫХ ИС

Лекция 1.

ВВЕДЕНИЕ. ПРОЕКТИРОВАНИЕ ЦИС: ЗАКАЗНОЙ И ПОЛУЗАКАЗНОЙ ВАРИАНТЫ

Развитие микроэлектроники демонстрирует рост сложности БИС и расширение области их применения, отсюда увеличение числа типономиналов изделий. Для массового производства .ИС и снижения их стоимости желательно, чтобы СБИС были универсальными и стоимость проектирования была ниже стоимости изготовления.

С другой стороны, размеры схем увеличиваются, кристалл становится структурной единицей, которую желательно специализировать.

Таким образом, СБИС должны быть и универсальными и специализированными.

К универсальным СБИС относятся, например, ЗУ и микропроцессоры (МП), их проектируют с самого начала с полупроводниковых приборов и заканчивая топологией кристалла. Такие схемы выпускают большими сериями, поэтому дороговизна проектирования снижается в пересчете стоимости на один бит или на одну функцию.

В технике всегда существует потребность в относительно небольших количествах специализированных БИС для конкретных системных применений, такие схемы называются специальными или заказными.

Заказные СБИС делятся на собственно заказные и полузаказные.

Заказные СБИС проектируются заново, начиная от создания библиотеки (custom) или на основе некоторой библиотеки (ASIC). Этап проектирования таких ИС занимает не менее года для «custom»-типа или 2-6 месяцев для «ASIC»-типа, капиталовложения при этом составляют, соответственно, от 1 M$ до 100K$.

Для проектирования полузаказных ИС используют некоторых полуфабрикат, поэтому отсутствует этап физического и электрического моделирования элементарных фрагментов. Технология изготовления ИС разработана вплоть до последних операций создания межсоединений. Правда, сохраняется этап моделирования либо всей схемы, либо ее узлов.

К полузаказным относят СБИС на таких полуфабрикатах, как транзисторные матрицы, вентильные матрицы, матрицы стандартных ячеек, программируемые логические матрицы (ПЛМ), ПЗУ.

Регулярный характер полузаказных БИС позволяет в значительной мере автоматизировать процесс проектирования, прежде всего, топологического для создания межсоединений.

Последние определения можно представить в виде некоторой классификации.

Специализированные

СБИС транзисторные матрицы

заказные полузаказные вентильные матрицы

ПЛМ, ПЗУ

custom ASIC

design

стандартные ячейки (узлы)

кремниевый компилятор

МЕТОДЫ ПРОЕКТИРОВАНИЯ специализированных полузаказных БИС.

Как видно из классификации , можно выделить следующие способы проектирования полузаказных БИС:

• на основе базовых матричных кристаллов (БМК), к которым могут относиться транзисторные или вентильные матрицы;

• на основе программируемых логических матриц (ПЛМ);

• на основе стандартных узлов;

• методом кремниевой компиляции.

БМК - это матрица нескоммутированных элементов, электрические связи формируются на этапе создания разводки.

ПЛМ - матрица элементов, в которой соединения можно создавать или разрушать по необходимости подачей программирующих сигналов (с использованием, например, МНОП -структур).

Стандартные узлы (ячейки) - метод проектирования, при котором используются непараметриз-ованные библиотеки стандартных ячеек.

Кремниевый компилятор (КК) - полностью автоматизированное преобразование поведенческих спецификаций СБИС к соответствующим геометрическим описаниям кристалла. Автоматическое преобразование языков высокого уровня в машинные языки. Результатом проектирования ИС при помощи КК является конструкторская документация к созданию слоев межсоединений - лэйаут (layout). Данный способ проектирования в данном курсе лекций не рассматривается, поскольку этот дорогой процесс требует соответствующего программного и аппаратного обеспечения. Метод КК чаще используется при проектировании сложных заказных БИС.

ДОСТОИНСТВА И НЕДОСТАТКИ проектирования полузаказных схем:

достоинства недостатки

- не нужно разрабатывать кристалл - потери площади кристалла

- высокая скорость проектирования - ограничение схемотехнических

- низкая стоимость проектирования вариантов

- высокий уровень контроля проекта

- возможность итераций

Лекция 2

ОСНОВНЫЕ ЛОГИЧЕСКИЕ ФУНКЦИИ.

Основные определения булевой алгебры.

В - некоторое множество, f и g - функции, для которых при x, y, z Bвыполняются следующие условия

Введем понятие пропозициональная форма. Пропозициональная форма - набор символов и отношение межде собой логических переменных, в простейшем варианте определения - связующая функция между переменными (объектами) в булевой логике, в которой переменные и сама функция принимают значения «0» и «1».

Чаще всего используют следующие функции:

а) повторение F = A, где А - переменная;

б) инверсия (отрицание, НЕ) F === A;

в) логическое сложение (дизъюнкция, ИЛИ) F = A + B = AB (функция двух переменных), выражение для большего числа переменных можно записать следующим образом F =,где - переменные;

г) логическое умножение (конъюнкция, И) F = A * B = A & B = AB (функция двух переменных), выражение для любого числа переменных - F = , где - переменные;

д) операция ИЛИ-НЕ F = (A + B) = ( стрелка Пирса); соответственно для нескольких переменных F = 

е) операция И-НЕ F = (штрих Шеффера), для нескольких переменных -

F = переменные;

ж) операция «эквивалентность» F = AB = (A  B) , функция принимает истинностные значения при равенстве значений А и В;

з) операция «неэквивалентность» F = A  B , функция принимает истинностные значения при неравенстве значений А и В («исключающее ИЛИ»);

и) операция «импликация» F = A  B , значение «ложно» функция принимает лишь при условии, когда А истинно, а В - ложно, то есть А  В = А &( В).

Следствие: если А и В пропозициональные формы (логические выражения), то и любые логические выражения с этими пропозициональными формами также являются логическими выражениями.

Любая пропозициональная форма может быть определена 3-мя связками: , &,  (НЕ, И, ИЛИ = инверсия, конъюнкция, дизъюнкция).

Любую функцию можно представить в нормальной конъюнктивной или нормальной дизъюнктивной форме, как сумму произведений либо произведение сумм прямых и инверсных значений переменных.

РАСПРОСТРАНЕННЫЕ АЛГЕБРАИЧЕСКИЕ ТОЖДЕСТВА

1. x + x = x * j * x * x = x - идемпотентность;

2. (x + y) + z = x + (y + z) - ассоциативность;

3. (x * y) = (y * x), (x + y) = (y + x) - коммутативность;

4. x (x + y) = x * y + x = x - поглощение;

5. (x + y) * z = x * z + y * z -дистрибутивность;

6. - правила Де-Моргана.

УСЛОВНО-ГРАФИЧЕСКИЕ ОБОЗНАЧЕНИЯ .

Приведем примеры обозначений логических элементов, наиболее часто применяемых в схемотехнике.

А F=

Повторитель АF ; инвертор А о F =; инвертор- > o

усилитель

А 0 F =

A A x_o

B & F=A*B B &⁰ F =&

И И-НЕ x_n-1 И для многих переменных

А А х₀

1 F=A+B 1 F= 1 F=

В В ^{0 0}

х_n-1

ИЛИ ИЛИ-НЕ ИЛИ-НЕ для многих переменных

х1 х1

 = 1

F =F

x2 x2

Исключающее ИЛИ, неэквивалентность.

Символ ^О - означает инверсию на выходе. В любой элемент может быть добавлен символ > , означающий усиление сигнала на выходе.

Пример. Приведем пример представления логической функции в пропозициональной форме и ее структурную схему.

Пусть известна таблица истинности для некоторой функции, которую нужно реализовать схемотехнически.

x1	x2	x3	F
0	0	0	0
0	0	1	0
0	1	0	1
0	1	1	0
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	0

F=P₁+P₂+P₃.

x1

^x o P₁

&

^x P₂ 1 F

x2 &

^{x O}

& P₃

x3 _{O x}

Основные логические функции можно проиллюстрировать примерами пересечения множеств:

«И» = & «ИЛИ» =  = +

А А

В В

«И-НЕ» =  (А&B) = A B «ИЛИ-НЕ» =  (А В) = А  В

В ВВВ В В

А А А

инверсия «НЕ» =  «импликация» = А&( В)

А А А В

Приведем примеры схемной реализации ряда распространенных логических функций с использованием трех основных логических действий (, , ):

« импликация» F =     *, таблица истинности функции:

A &

A	B	F
0	0	0
0	1	0
1	0	1
1	1	0

B _{O O} f =(АВ)=

«тавтология» F = А =1, А

&

О О 1

при помощи последней схемы можно выполнить

схему формирования сигнала, введя линию задержки из нечетного числа инверторов:

А

& o

Л.З. о

«Бистабильная ячейка» F =

A F

Бистабильная ячейка - это простейший элемент памяти, который является основой широко распространенных триггерных схем и оперативных запоминающих устройств. Приведем примеры условно-графических обозначений некоторых триггеров.

RS- триггер . o

R & Q R Q

RS-tr

S & S ^O

Логические элементы в RS-триггере могут быть как И-НЕ, так и ИЛИ-НЕ типа, выходные значения функций меняются при этом с точностью до инверсии. Триггеры на И-НЕ-базисе управляются положительными сигналами, а на ИЛИ-НЕ-базисе - отрицательными.

DC-триггер. Тактируемый триггер задержки выполняет следующую функцию:

D Q

D Q

При С = 0, - это элемент памяти, С о =

а при С = 1, . C ^O

Элемент памяти изображается обычно с соответствующими адресной (словарной) и разрядной (числовой) шинами управления: АШ(СШ)

ЭП РШ(ЧШ)

Лекция 3

ПРОЕКТИРОВАНИЕ СТАНДАРТНЫМИ ЯЧЕЙКАМИ (СЯ)

НА БАЗОВЫХ МАТРИЧНЫХ КРИСТАЛЛАХ (БМК)

Библиотека элементов на БМК

При проектировании изделий на БМК методом стандартных ячеек заранее известен тип стандартной, или базовой, или библиотечной ячейки . Простейшая библиотечная (базовая) ячейка (БЯ) может представлять собой набор транзисторов (4-8-12), не соединенных между собой.

В стандартных ячейках и в БМК шины питания расположены на одном уровне:

шины питания

СЯ СЯ БЯ1 БЯ2

Стандартные ячейки (СЯ) представляют собой завершенные схемотехнические элементы (2-И-НЕ, 3-ИЛИ-НЕ,  , триггер и т.д. Их использование при проектировании более сложных схем позволяет минимизировать площадь кристалла, но это и более дорогой метод.

Более дешевый способ проектирования на библиотечных (базовых) элементах БМК. Можно выделить 4 уровня элементов БМК на примере КМДП-элементной базы:

0 -й уровень - отсутствует связь между стоками и затворами;

1-й уровень - существует связь между затворами и стоками;

2-й уровень -существуют секционные элементы (СЯ);

3-й уровень - существуют функционально законченные устройства на кристалле типа ПЗУ, ОЗУ, ПЛМ,

АЛУ и т.д.

Простейшая ячейка БМК - это библиотечный элемент (БЯ) из несоединенных транзисторов:

p p на показанной БЯ1 можно построить 2 инвертора,

БЯ1 элементы 2-И-НЕ, 2-ИЛИ-НЕ.

n n

При помощи показанного элемента БЯ1 можно также построить еще один элемент: так называемый ключ (проходной ключ).

. . . . . . . . . . . . . . . . . . . . . . . . . .

Лекция 8(9)

ТЕХНИЧЕСКОЕ ЗАДАНИЕ

При проектировании заданного устройства разработчик и заказчик заключают договор, в котором присутствуют следующие разделы:

1. Цель, наименование работы.

2. Исполнитель, заказчик (гражданский, военный).

3. Финансирование.

4. Сроки: начало, окончание (0,5-3 года).

5. Технические характеристики, техническое задание (ТЗ)

• качественное описание устройства,

• функциональная схема на любом базисе,

• функциональная схема на заданном базисе серии,

• поведенческое описание на языке VHPL,

VHPL: поведенческое описание

adder 

input регистры, вентили

output 

топология



БИС

• технические требования: - алгоритм, электрическая схема,

- статические характеристики,

- динамические характеристики,

технические требования - для нормальных условий (НУ),

- предельные,

- предельно-допустимые.

Пример: U_ИП

T = -10⁰ ... + 60⁰ С , (- 60⁰ ...+85⁰, 125⁰ для военной приемки),

I_ст ~ 1 мкА,

I_дин , I_дин=,

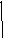
I

_О

t

Общий ток в схеме ,

• внешние воздействующие факторы (ВВФ), испытание в агрессивной среде,

• климатические испытания,

• механические воздействия, давление,

• радиационные воздействия, устойчивость I У, II У, III У - чем выше стойкость, тем лучше,

• конструктивные требования: размеры кристалла, число выводов на кристалле, шаг выводов, тип корпуса (пластмассовый - гражданский, металлический - военный).

Пример. Микропроцессор на БМК (1515), 15 млн. руб. за 20 образцов, 1 млрд. руб. за 100 образцов. (Цены 1997 г.)

СОПУТСТВУЮЩИЕ ДОКУМЕНТЫ

Цикл изготовления заказанного устройства можно представить схематично:

заказчик

разработчики

аттестация

завод-изготовитель

Аттестация элементов вводится разработчиком САПР и прилагается к проекту в виде книги.

Аттестация представляется для всех разновидностей изменения

• внешних факторов (U_ИП, T, радиация и т.д.),

• внутренних факторов (С_нагр, t, электрофизических параметров k, U_пор, W, L и т.д.),

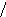
• способы переключения для лучшего (С_нагр1), типового (С_нагр2) и худшего случаев (С_нагр3):

01

00 1 0

01

₀

01 1

t_зд

	UИПmin															UИПтип										UИПmax
Способ переключения	Снmin				Cнтип					Снmax
ni	Tmin	Tтип	Tmax
ni

Способы переключения рассчитываются, исходя из числа выводов элементов N:

варианты: 1) (111)  (011),

2. (111)  (001),

3. (111)  (000) и т.д..

Число вариантов проекта очень велико, его формирует количество задаваемых параметров. Например, величина U_пор для различных вариантов схемы может отличаться примерно на 1 В даже теоретически и может быть отрицательной для n-канального транзистора ( в цепи такого быть не может).

Проектирование быстродействия схемы обосновывается по тестовой схеме кольцевого генератора, исследуемого при всех внешних воздействиях.

Аналитически вместо таблицы можно проводить расчеты по следующей формуле:

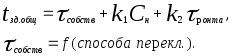
Рассчитав такую величину, можно рассматривать элементы схемы как безынерционные в соответствующем включении:

t_зд

Э Э

t_зд

Разработанное устройство, пройдя классификационные испытания (К1.....К25),

периодические испытания (П1......ПN),

приемо-сдаточные испытания (ПСИ),

получает справку о соответствии

№ по ТЗ	№ протокола	сответствие
1. UИП, 5 В
2. .....

В справке представлены следующие данные: 1. Долговечность.

2. Надежность.

3. Температурный диапазон.

4. Предельно допустимые параметры.

5. Ударные испытания

6. и т.д.

В конце справки обязательны подписи членов Комиссии во главе с председателем, (состав комиссии не менее 6 человек ), представителя завода изготовителя, главного конструктора, заказчиков и др.

На основании заключения справки изделию присваивается категория

Б - схема не освоена,

А - после испытаний годна.

Л Е К Ц И Я

Тестопригодность Терминология, классификация.

Тестовое диагностирование – обнаружение неисправностей элементов ИС вследствие дефектов производства, эксплуатации или старения . Тестирование происходит по результату: проходит или не проходит сигнал.

Ремонтопригодность схем – это характеристика схем, включающая в себя диагностирование вида «поиск дефекта»: проверка исправности и локализация неисправности.

Неисправность может быть вызвана физическим дефектом, например, обрывом. Проявление неисправности характеризуется логическим состоянием схемы, например, типа зависания логического состояния. Поведение неисправностей адекватно отображается моделированием по логическим функциям: короткое замыкание (КЗ), проводное И, ИЛИ, обрыв (ХХ).

Первичные входы. (ПВх) – входы, чьими логическими состояниями можно непосредственно упрвлять.

Первичные выходы (Пвых) - выходы, которые можно непосредственно наблюдать.

Тест (тестовый набор) - определенное множество сигналов на ПВх и ожидаемых реакций на Пвых. Покрытие неисправностей – характеризует множество неисправностей, обнаруживаемых либо отдельным тестом либо их множеством.

Исправность ИС проверяется автоматическими диагностирующими устройствами, тестерами. Они действуют в соответствии с программой.

Программное тестирование состоит из 3-х процедур:

1. генерация тестов;

2. оценка эффективности тестов;

3. реализация тестового диагностирования.

1.Генерация тестов – процедура нахождения множества тестовых входных наборов и ожидаемых реакций исправного устройства, обеспечивающего покрытие неисправностей из заданного списка. Цели такой процедуры:

• изменение сигнала в определенном узле схемы,

• установление активизированного пути для определенной неисправности (по узлам),

• испытание подсхемы во всех ее состояниях.

Облегчение или усложнение процесса генерации тестовых наборов связано с управляемостью и наблюдаемостью схемы. Чем выше значения этих параметров, тем проще нахождение, проявление и транспортировка неисправностей.

2. Эффективность тестов – процедура для количественного определения степени покрытия множеством тестов заданного списка неисправностей (множества одиночных неисправностей вида «неконтролируемый «0» [н.к.0]) и н.к.1 на всех соединениях схемы. Уровень покрытия можно оценить моделированием.

Метод физического моделирования при помощи стендовых электрических испытаний ограничен возможностями доступа к элементам внутри ИС и особенностями схемы. Пример: для моделирования неисправности типа н.к.0 можно заземлить выход ТТЛ- схемы, но нельзя для случая н.к.1 соединить выход схемы с шиной питания, даже через резистор, - повреждения в схеме могут быть необратимы, вместо тестирования получим разрушение.

Практически задача решается логическим моделированием неисправности, неисправности из списка вводятся в модель схемы последовательно или комбинациями (параллельно).

3. Реализация тестового диагностирования - физический процесс тестирования. Проблемы могут быть связаны с ограничениями возможностей аппаратуры (скорость подачи тестов, ограниченность технических приспособлений…). Поиск неисправностей затруднен в цепях с обратными связями, если элементы замкнуты друг на друга и т.п.

Перечисленные процедуры требуют больших затрат на ЭВМ, специальные программы, обучение персонала, обслуживание стендов тестеров и т.д. Затраты можно снизить, если проектировать схемы с улучшенной тестопригодностью.

Тестопригодность – приспособленность схемы к обнаружению неисправностей, их локализации и реализации тестового диагностирования в пределах допустимых финансовых затрат. Нужно сокращать затраты в любом их перечисленных разделов: на ЭВМ, программы, время тестирования, обучения, обслуживания и т.д.

Различают три подхода к проектированию тестопригодных схем:

• численная оценка управляемости и наблюдаемости, количественная мера тестопригодности;

• структурное проектирование (иногда самотестируемых) схем с использованием свойств сканируемого пути с простотой доступа к внутренним точкам устройства. Эффективные методы генерации тестов, реализующих методы сканирования;

• разработка практических указаний для сокращения затрат на процедуры генерации тестов и реализацию тестирования.

Анализ тестопригодности. Сиcтема CAMELOT.

Количественные оценки тестопригодности могут быть проведены до генерации тестов и могут быть сделаны счетным или алгоритмическим способом.

Счетные оценки. Главное – идентифицировать особенности схемы, характеризующие тестопригодность. Эти характеристики задаются набором показателей. Подсчитывают показатели, ухудшающие и улучшающие тестопригодность, их комбинации дают оценку тестопригодности. В этой методике не обязательно использовать ЭВМ, возможно дать рекомендации на последнем этапе проектирования схемы, например, по секционированию, расположению контактных площадок, разъемов и т.д. Оценки достаточно грубые.

Алгоритмические оценки - реализуются программно, в основе лежит анализ топологии. Анализируется каждый узел, строятся сечения схемы по уровню тестопригодности (гистограммы), находят слабые места. Основными параметрами такого анализа являются управляемость и наблюдаемость.

Управляемость (CY) - это простота решений задач подачи теста в определенный узел.

Наблюдаемость (OY) – это реагирование на выходах подсхемы в заданном состоянии окружения/

Тестопригодность любого узла есть функция управляемости и наблюдаемости этого узла:

TY(узла) = CY(узла)OY(узла).

Управляемость.

В системе CAMELOT управляемость CY принимает относительные значения от 0 до 1.

Значение CY = 1 – максимальная величина параметра соответствует первичному входу: можно установить любое логическое состояние.

Значение CY = 0 - узел не может быть установлен в одно из двоичных состояний.

Остальные узлы характеризуются значениями CY между этими границами.

Теория передачи значений CY через элементы устройства.

Рассмотрим устройство.

Если входы управляются непосредственно, входы

то управляемость выходов должна отражать

способность устройства к установке на каждом выходы

выходе 0 или 1 по логической передаточной функции.

В общем случае управляемость входов может быть не 100%-ной, поэтому управляемость выходов должна учитывать и способность выполнять логическую функцию и значения управляемости входов:

СY (вых.узла) = CTF  f{ CY( вх. узлов)},

CTF – controlability transfer factor – коэффициент передачи управляемости устройства по данному выходу.

CTF – мера степени различия способности генерировать на данном выходе ” 1” от способности генерировать на данном выходе “ 0 “. Данный коэффициент зависит только от логической функции, реализуемой устройством:

N(0) – число всех способов установки “0” на данном выходе устройства,

N(1) - число всех способов установки “1” на данном выходе.

ПРИМЕРЫ.

1. При N(0) = N(1) CTF = 1, например, в схемах эквивалентности и неэквивалентности ().

2. При N(0) = 0, N(1) = 0 CTF = 0 - неуправляемость логическим состоянием, такое маловероятно.

3. Инвертор: N(0) = 1, N(1) = 1: CTF = 1.

4. Схема 2И-НЕ. N(0) = 1, N(1) = 3: CTF = 1-2/4 = 0.5.

5. Схема 2ИЛИ-НЕ. N(0) = 3, N(1) = 1: CTF = 1-2/4 = 0.5.

6. Схема 3И-НЕ. N(0) = 1, N(1) = 7: CTF = 1-6/8 = 1-0.75 = 0.25.

и т.д.

Вычисление CTF для схем с памятью.

Рассмотрим триггерную схему с синхронными и асинхронными управляющими логическими переменными JKT – триггер:

P

J PR

T

K

CLR

C

Логическая функция JK- триггера Qⁿ⁺¹ = JQⁿ + KQⁿ.

C учетом сигналов предзаряда Р (PR), сброса С (CLR) и синхросигнала Т ( Т=1 – условие присутствия отрицательного фронта тактового сигнала) получим:

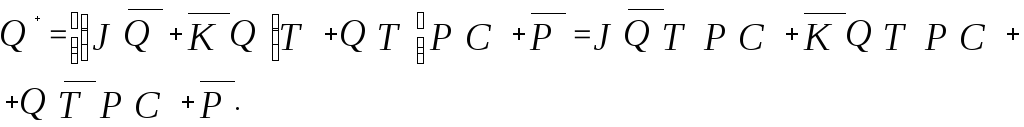
Составим карту Карно по полученной функции. Количество переменных – 6, число минтермов 2⁶ = 64. Можно вычислить N(1), если рассчитать количество минтермов со значением Q⁺ = 1.

Главное, чтобы подмножества минтермов не пересекались друг с другом. По карте N(1) = 40.

C=0 C=1

CJK

TPQ+	000	001	011	010	110	111	101		100
000	1*	1*	1*	1*	1*	1*	1*	1*
001	1	1	1	1	1	1	1	1
011					1	1	1	1
010
110					1	1
111					1			1
101	1	1	1	1	1	1	1	1
100	1*	1*	1*	1*	1*	1*	1*	1*

Звездочками помечены запрещенные состояния.

Неустойчивые состояния выходов триггера возможны при следующих сочетаниях входных переменных:

P = 0 C = 1 Q = 0,

P = 1 C = 0 Q = 1,

P = 0 C = 0 Q = 0,

Итого 2³ = 8 запрещенных наборов. Для 3-х сочетаний переменных всего 83 = 24 минтерма.

По карте Карно видно, что на 1- ные минтермы попало 16 запрещенных состояний, осталось

N(1) = 40 – 16 = 24. Запомним N(1) = 24.

{ Можно провести расчет единичных минтермов при помощи алгебраического выражения, воспользовавшись следующей теорией:

лемма. Если Q⁺ - функция n переменных, а i- й терм содержит j переменных (j  n), то число значений функции Q⁺ = 1, представляемое i- м термом, равно 2^n-j.

Перед расчетом по этой формуле необходимо проверить подмножества минтермов на непересечение, для чего проводится следующая процедура.

процедура. Пусть два конъюнктивных терма Т1 и Т2 не удовлетворяют условию непересечения, и пусть

RC = T1/T2 - разность множеств переменных из этих термов.

Разность множеств Т1/Т2 – множество элементов, принадлежащих Т1, но не принадлежащих Т2, например:

T1 = { a,b,c,d}, T2 = { b,c,e }, T1/T2  T2/T1.

Пусть RC – непустое множество переменных X1, X2…..Xn. Преобразование пары Т1 и Т2 в совокупность непересекающихся подмножеств описывается операцией расширения:

то есть мы вводим в один из термов недостающую переменную, при этом автоматически исключаются из него минтермы, входящие в другой терм.

Проанализируем логическое выражение для функции JKT- триггера по этой процедуре:

каждый терм – это блок разбиения ( сшивания, см. карту Карно ), таким образом, в терме

В сумме число единиц N(1) = 40, как и в расчете по карте Карно. }

Рассчитаем число нулей на выходе данной схемы с учетом известного числа разрешенных переходов и числа единичных состояний.

Рассчитаем теперь коэффициент передачи управляемости для триггерной схемы:

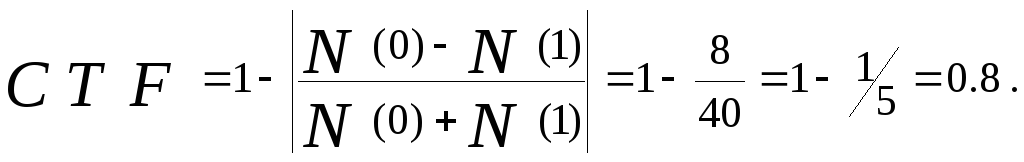
Схема симметрична, поэтому по другому выходу получим тот же результат для CTF.

Вычисление управляемости.

Пусть в нашем устройстве n входов и m выходов. Любой вход влияет на состояние любого выхода. Управляемость выхода может существенно отличаться от управляемости соседнего выхода, поэтому в общем виде можно записать:

где f(CY(n_i)) –математическая функция, пропорциональная среднему арифметическому и/или среднему геометрическому значений управляемостей входных сигналов различных типов.

Для асинхронных сигналов функция f(CY(..)) – это среднее арифметическое управляемостей входных узлов, запитываемых асинхронными сигналами; для синхронных сигналов такая функция представляет собой произведение величины управляемости тактирующего сигнала (синхросигнала) на среднее значение управляемостей входных тактируемых сигналов.

В общем виде для схем с различными типами входных сигналов получаем:

CY(выходов) = CTF(выходов)  f(CY(входов)),

Для предыдущего примера схемы JKT- триггера:

число асинхронных входов i = 2 (сигналы предзаряда или выборки PR и сброса CLR),

число синхронных входов j = 3 (тактовый сигнал Т и информационные сигналы J и K).

Рассчитаем управляемость схемы. Зададимся исходным состоянием: пусть на входы сброса и предзаряда ничего не подано, они пассивны: CY(PR) = CY(CLR) = 0, а синхронизирующий тактовый сигнал (отрицательный фронт) присутствует: CY(T) = 1. Коэффициент передачи управляемости триггера рассчитали ранее CTF() = 0.8,

CY(Q⁺) = CTF(выхода)  f(CY(входов)) =

Логические состояния на входах фиксируются, при этом получим разные значения управляемости схемы для следующих сочетаний значений логических переменных:

CY(J) = CY(K) = 0 : CY(Q⁺) = 0.8  0.2  0 = 0,

CY(J) = 1, CY(K) = 0 : CY(Q⁺) = 0.8  0.2  1 = 0.16,

CY(J) = CY(K) = 1 : CY(Q⁺) = 0.8  0.2  2 = 0.32.

Управляемость в схемах с обратными связями.

Вычисление управляемости в таких схемах выполнять труднее, нужно решать систему уравнений. Рассмотрим пример простейшего RS- триггера.

СY=1 1

V1 CY=y