76. Приведенная длина винта резьбовой передачи при расчете его на устойчивость.

Коэффициент μ - это число, показывающее, во сколько раз следует увеличить длину шарнирно опертого стержня, чтобы критическая сила для него равнялась критической силе стерж­ня длиной l в рассматриваемых условиях закрепления (Определение из сопромата).

μl – приведенная длина стержня, где l – длина неопорного участка (за расчетный принимают крайнее положение гайки, когда винт нагружен по максимальной длине), используемая при расчетах, в зависимости от способа закрепления винта:

Расчет можно проводить двумя методами.

1) расчет по коэффициенту понижения допускаемого напряжения

- A – площадь сечения винта по внутреннему диаметру, [σ]_сж – допустимое напряжение сжатия.

φ – коэффициент понижения допускаемого напряжения, который выбирают по таблице в зависимости от гибкости винта.

- гибкость, гдеl – длина неопорного участка (за расчетный принимают крайнее положение гайки, когда винт нагружен по максимальной длине).

- радиус инерции сечения, J – момент инерции сечения,, μ – коэффициент приведенной длины, учитывающий способ закрепления концов винта.

2) метод Эйлера определения критической силы

S – коэффициент запаса.

77. Гибкость винта. Определение гибкости винта и ее влияние на величину критической силы, действующей вдоль оси винта.

- гибкость, гдеl – длина неопорного участка (за расчетный принимают крайнее положение гайки, когда винт нагружен по максимальной длине).

- радиус инерции сечения, J – момент инерции сечения,, μ – коэффициент приведенной длины, учитывающий способ закрепления концов винта.

- следовательно, при увеличении гибкости критическая сила снижается.

78. Использование объединенного условия прочности и устойчивости сжатых стержней в расчетах резьбовых передач.

Расчет тела винта, нагруженного силой затяжки и моментом трения в резьбе:

За счет растяжения в теле винта возникает напряжение

За счет существования вращающего момента в резьбе возникает напряжение τ.

Для расчета такого напряженного состояния применим энергетическую теорию прочности:

где - нормальные напряжения,- максимальные касательные напряжения,- момент в резьбе,- момент сопротивления кручению.

Тогда, подставив эти значения, получим

Т.к. все резьбы геометрически подобны, то

Проверочный расчет на срез и смятие проводят в тех случаях, когда одна из деталей с резьбой выполнена из материала менее прочного, чем у другой детали.

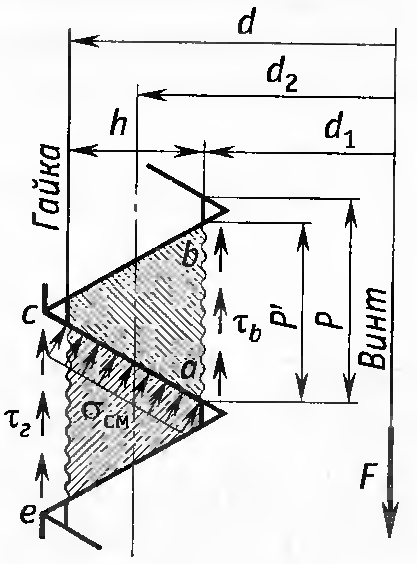
Срез резьбы винта происходит по диаметру d₁, т.е. для резьбы винта

Срез резьбы гайки происходит по диаметру d, т.е. для резьбы гайки

где H – высота гайки, k=P'/P – коэффициент полноты резьбы, k_m – коэффициент, учитывающий неравномерность распределения нагрузки по виткам резьбы из-за ошибки шага.

Напряжение смятия в резьбе

где z=H/P – число витков резьбы гайки; - напряжение смятия для менее прочной детали резьбовой пары.

Расчет тела винта на устойчивость:

- A – площадь сечения винта по внутреннему диаметру, [σ]_сж – допустимое напряжение сжатия.

φ – коэффициент понижения допускаемого напряжения, который выбирают по таблице в зависимости от гибкости винта.

- гибкость, гдеl – длина неопорного участка (за расчетный принимают крайнее положение гайки, когда винт нагружен по максимальной длине).

- радиус инерции сечения, J – момент инерции сечения,, μ – коэффициент приведенной длины, учитывающий способ закрепления концов винта.

Если гибкость >100, то используют формулу Эйлера

S – коэффициент запаса.