Лекции по СПиУ (заочникам)

1. Минимизация времени выполнения проекта при неизменной его стоимо-

сти.

2. Минимизация стоимости проекта при неизменном времени его выполне-

ния.

Комплексная оптимизация сетевого графика представляет собой нахождение оптимального соотношения времени выполнения проекта и его стоимости с учетом целей проекта.

При использовании метода «время-стоимость» предполагают, что уменьшение продолжительности работы пропорционально возрастанию ее стоимости. Длительность выполнения каждой работы варьируется в следующих пределах:

делах:

21

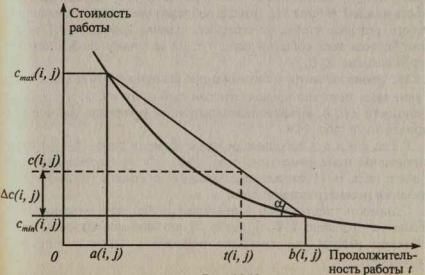
Рис. График зависимости продолжительности и стоимости работы

Из приведенного графика видно, что возможно снижение затрат на выполнение работы в случае увеличения ее длительности. Исходя из этого, одним из самых очевидных способов уменьшения стоимости проекта (частичной оптимизации сетевого графика) будет увеличение длительности работ, не лежащих на критическом пути, и имеющих резервы времени.

Рассмотрим, как будут рассчитываться длительности работ и их стоимость в случае такой оптимизации сетевого графика.

Продолжительность работ целесообразно увеличивать таким образом, чтобы не изменить ранние (ожидаемые) сроки наступления всех событий сети, т.е. на

мальная продолжительность работы должна быть определена по формуле:

длительности рассчитывается по следующей формуле:

22

где

– величина, на которую уменьшится стоимость работы при увеличении ее длительности;

- коэффициент изменения затрат от изменения длительности работы

;

- время, на которое увеличилась продолжительность работы.

где – стоимость работы при наиболее вероятной ее продолжительности.

Стоимость проекта после оптимизации составит:

где - стоимость проекта до оптимизации.

Результаты расчетов необходимо представить в следующей таблице:

Условный пример. Необходимо провести частную оптимизацию сетевого графика, исходные данные приведены в таблице.

23

24

25