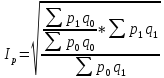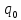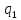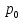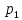Статистика Лекции

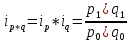
Общие индексы, правила построения общих индексов.

Общие индекс(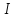) применяют доя оценки изменения по времени, в пространстве или по сравнению с планом сложных экономических явлений.

Для построения общих признаков необходимо знать индексную систему. Она включает два момента:

• Показатель изменения которого нас интересует непосредственно называется индексируемый показатель. Если индексируемый показатель находится в числителе индексного отношения, то это отчетное значение, а если в знаменателе, то базисное значение.

• Показатель изменений которого нас не интересуют, называется статистический вес. Он необходим для приведения в соизмеримый вид, непосредственно несоизмеримых элементов, сложного экономического явления. Статистический вес и в числители и в показателе индексного отношения используется либо на уровне отчетного, либо на уровне базисного периода. Статистический вес применяется на уровне текущего или базисного периода в зависимости от того, первичный это показатель или вторичный.

К первичным(количественные, объемные) показателям относят физический объем.

Вторичные(качественные) показатели – цена, себестоимость, производительностью, d(тарифы)

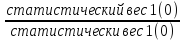
При построении общих признаков необходимо соблюдать следующие правила.

• Если индексируется первичный показатель, то в качестве статистического веса используется вторичный показатель, на уровне базисного периода.

Пример, получим общий индекс физического объема.

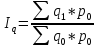– общий индекс физического объема.(1)

• Если индексируется вторичный показатель, то статистическим весом является первичный показатель на уровне отчетного периода.

Получить общий индекс цены:

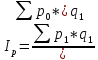– общий индекс цены, (%, разы).(2)

Общие индексы полученные выше называются агрегатными, а их построение называется синтетическая концепция.

Синтетическая концепция дает качественную оценку изменения сложного экономического явления. На её основе можно получит аналитическую концепцию.

На основе расчета общих индексов дается количественная оценка явления и влияние факторов на изменение сложных экономических явлений.

Пример. Из формулы 1 получить аналитическую концепцию.

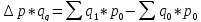(3)

Абсолютное изменение товарооборота, под влиянием физического объема.

На основе формулы 2 получим абсолютное изменение товарооборота под влиянием цены.

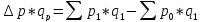(4)

Между вышеперечисленными индексами существует взаимосвязь:

• Индекс товарооборота равен произведению общего индекса цены, на общий индекс физического объема.

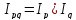– взаимосвязь индексов.(5)

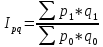- общий индекс товарооборота.(6)

Абсолютное изменение товарооборота, под влиянием и цены и физического объема. На основе формулы 6.

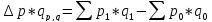
На основе имеющихся данных.

Рассчитать общий индекс цены, товарооборота. Определить влияние факторов на изменение товарооборота.

Вид	Объем реализации, тыс. шт.			Цена, руб.
	Базисный период,	Отчетный период,	Базисный период,		Отчетный период,
1	8	10	10		9,5
2	20	22	8		7
3	16	18	5		5

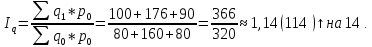
Объем реализованной продукции увеличился в целом на 14%.

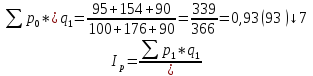
Цена на все реализованные товары снизилась на 7 %.

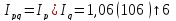
Влияние цены на изменение товарооборота.

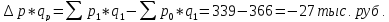
Товарооборот снизился на 27 тыс. рублей под влиянием снижения цены на 7%.

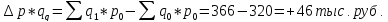
Товарооборот увеличился на 46 тыс рублей под влиянием увеличения объема реализованной продукции на 14%.

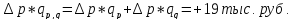
Товарооборот в целом на все виды продукции увеличился на 19 тыс руб., под влиянием увеличения объема.

3. Агрегатные и средние индексы.

Общие индексы рассмотренные выше, называются агрегатными. Для их построения необходима информация о значениях индексируемого показателя в отчетном и базисном периодах и информация о значениях статистического веса, что на практике не всегда известно.

3.1. Если исходная информация не позволяет сконструировать общие индексы в агрегатном виде, то прибегают к построению средних индексов(это средний арифметический общий индекс и средний гармонический общий индекс).

Преобразуем агрегатный индекс физического объема в средний индекс.

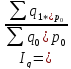(1)

Если информация о показателях известна только на уровне базисного периода, то преобразование будет следующее: зная, что 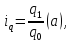можно выразить 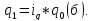Подставим (б) в формулу изменения физического объема 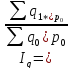и получим: 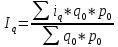-средний арифметический общий индекс физического объема.

3.2. Если информация о показателях только на уровне отчестного периода, то на основе формулы(2) можно получить средний общий индекс:

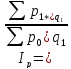(2)

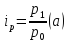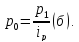Зная, что , можно выразить Подставим (б) в формулу цены и получаем: 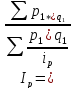- средний гармонический индекс изменения цены.

Имеются данные о расходах и об изменении тарифных ставок на ж.д.

1)Определить изменение тарифных ставок в целом на по трем наименованиям грузов;

2)Определить изменение доходов, обусловленных изменением тарифных ставок.

Наименование груза
	Базисный период	Отчетный период

1)Доходы = d*q (d-тарифная ставка)

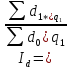-общий индекс тарифной ставки.

Подставляем

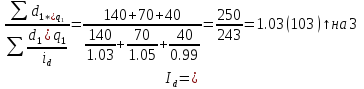
Тарфиная ставка в целом на все виды грузов увеличилась на 3%.

2)

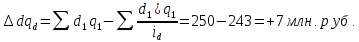
Доходы в целом увеличились на 7 млн. руб. под влиянием увеличения тарифной ставки на 3%.

4. Сфера применения общих индексов.

Общие индексы широко применяются в статическом анализе для решения различных задач:

1. Для качественной оценки сложных экономических явлений. При этом рассматривают их изменение по сравнению с планом.

2. Общий индекс позволяет установить влияние фаткоров на изменение результативных показателей. При этом дается количественная оценка влияния каждого фактора.

В настоящее время широко применяются следующие способы оценки изменения цен:

1. Расчет общего индекса по методике Пааше.

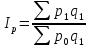(статистический вес «1»)

2. Методика Ласпейреса.

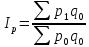(статистический вес «0»)

3. Методика Фишера.(д/з)