
Вопросы к экзамену для 1 курса 1 семестр
.docСписок теоретических вопросов к экзамену по высшей математике,
курс I
-
Понятие матрицы. Типы матриц. Способы представления матриц.
-
Арифметические операции над матрицами. Свойства линейных операций.
-
Произведение матриц. Свойства произведения. Транспонирование матриц.
-
Элементарные преобразования матриц. Эквивалентные матрицы.
-
Понятие определителя матрицы. Вычисление определителей второго и третьего порядка.
-
Основные свойства определителей.
-
Миноры и алгебраические дополнения матриц.
-
Теорема Лапласа. Пример применения.
-
Понятие обратной матрицы. Методы вычисления обратных матриц.
-
Ранг матрицы. Методы вычисления ранга.
-
Системы линейных алгебраических уравнений (СЛАУ). Основные определения и типы.
-
Ранг расширенной СЛАУ. Теорема Кронекера-Капелли.
-
Решение однородных СЛАУ.
-
Решение СЛАУ матричным методом.
-
Решение СЛАУ методом Крамера.
-
Решение СЛАУ методом Гаусса.
-
Общее понятие вектора. Вектор в N-мерном пространстве. Линейные операции над векторами.
-
Скалярное произведение векторов. Свойства скалярного произведения.
-
Определение угла между векторами. Ортогональные вектора.
-
Действия над векторами, заданными в геометрической форме. Взаимное расположение векторов.
-
Прямоугольные координаты в пространстве. Расстояние между двумя точками в пространстве. Координатная форма вектора. Скалярное произведение в координатной форме.
-
Векторное произведение, геометрическая интерпретация. Основные свойства векторного произведения. Векторное произведение в координатной форме.
-
Смешанное произведение векторов. Геометрическая интерпретация.
-
Линейная зависимость векторов. Свойства линейно зависимой системы векторов.
-
Понятие базиса в векторном пространстве. Разложение вектора по базису.
-
Понятие постоянной и переменной величин. Определение функции. Способы задания функций.
-
Основные задачи аналитической геометрии. Расстояние между двумя точками на плоскости, деление отрезка в заданной пропорции, площадь треугольника с заданными вершинами.
-
Геометрическое место точек. Уравнение линии на плоскости. Уравнение прямой на плоскости. Виды расположения прямой. Каноническое уравнение прямой и его частные случаи.
-
Пучок прямых, проходящих через заданную точку. Прямая, проходящая через две заданные точки. Уравнение прямой с угловым коэффициентом.
-
Взаимное расположение прямых на плоскости. Геометрическая интерпретация решения СЛАУ.
-
Основные характеристики функций. Понятие обратной функции.
-
Основные элементарные функции и их графики.
-
Понятие сложной функции. Способы преобразования
-
Приращение аргумента и приращение функции.
-
Определение предела функции в точке.
-
Основные теоремы о пределах. Теорема о двух милиционерах.
-
Односторонние пределы. Пределы функции при
 .
. -
Понятие числовой последовательности. Понятие сходимости последовательности. Свойства сходящихся последовательностей.
-
Бесконечно большие и бесконечно малые функции. Основные свойства и связь.
-
Вычисление пределов функций. Раскрытие неопределенностей вида
 .
. -
Вычисление пределов функций. Раскрытие неопределенностей вида
 .
. -
Замечательные пределы. Основные соотношения при использовании замечательных пределов.
-
Сравнение бесконечно малых функций. Понятие эквивалентных бесконечно малых и их свойства.
-
Определение непрерывности функции в точке. Свойства функций, непрерывных в точке. Непрерывность элементарных функций.
-
Понятие точки разрыва. Классификация точек разрыва.
-
Определение касательной к кривой в точке.
-
Определение производной функции в точке. Односторонние производные функции в точке. Геометрический смысл производной.
-
Связь между непрерывностью и дифференцируемостью функции. Основные теоремы о производной.
-
Производные элементарных функций. Вывод производных для
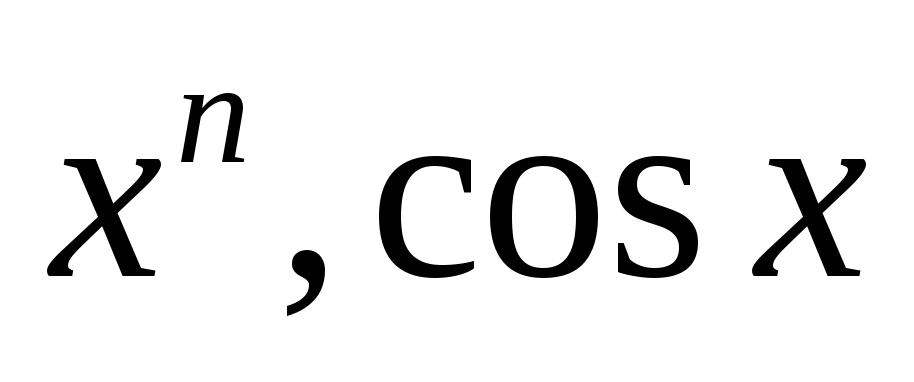 .
. -
Производные элементарных функций. Вывод производных для
 .
. -
Производные элементарных функций. Вывод производных для
 .
. -
Производная обратной функции. Вывод производной
 .
. -
Производная обратной функции. Вывод производной
 .
. -
Производная сложной функции.
-
Дифференцирование неявно заданных функций. Логарифмическое дифференцирование.
-
Производные высших порядков.
-
Производные высших порядков.
-
Понятие дифференциала функции. Геометрический смысл дифференциала.
-
Основные теоремы о дифференциалах. Инвариантность дифференциала. Дифференциалы высших порядков.
-
Применения дифференциала к приближенным вычислениям.
-
Теоремы Ферма, Ролля, Лагранжа и Коши и их геометрическая интерпретация.
-
Правило Лопиталя. Условия применения и формы представления.
-
Понятие монотонности функции, связь с касательными. Необходимое и достаточное условия.
-
Экстремумы функции и их типы. Понятие гладкой функции. Необходимое условие существования экстремума.
-
Понятие стационарных и критических точек функции, геометрическая интерпретация.
-
Первое и второе достаточные условия существования экстремума.
-
Понятие выпуклой функции, типы выпуклости. Точки перегиба.
-
Необходимое и достаточное условие существования точки перегиба.
-
Понятие асимптоты графика функции. Типы асимптот и способы их построения.
-
Общая схема исследования явной функции и построения ее графика.
СОДЕРЖАНИЕ ЭКЗАМЕНАЦИОННОГО БИЛЕТА
-
Два теоретических вопроса.
-
Шесть задач по темам:
-
матричное исчисление
-
векторная алгебра
-
вычисление пределов
-
вычисление производных
-
исследование функций
-
аналитическая геометрия
Производные
-

-
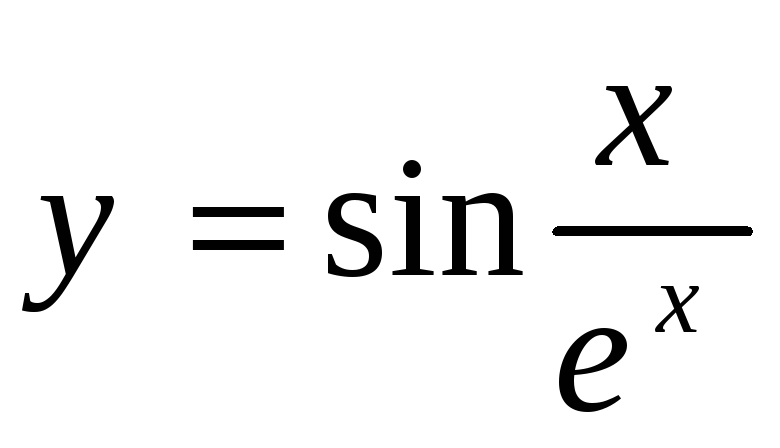
-

-
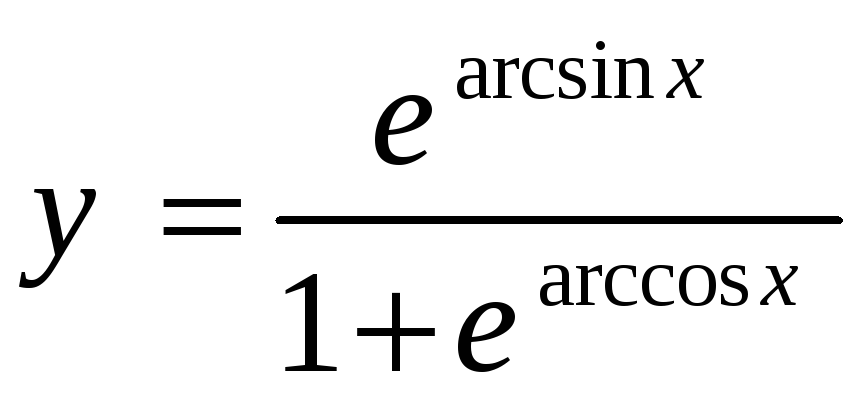
-
 .
. -
 .
. -
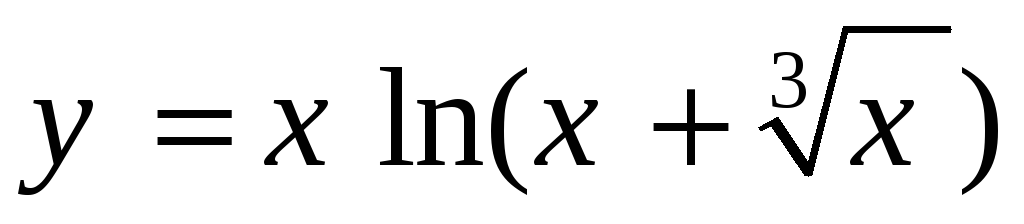
-
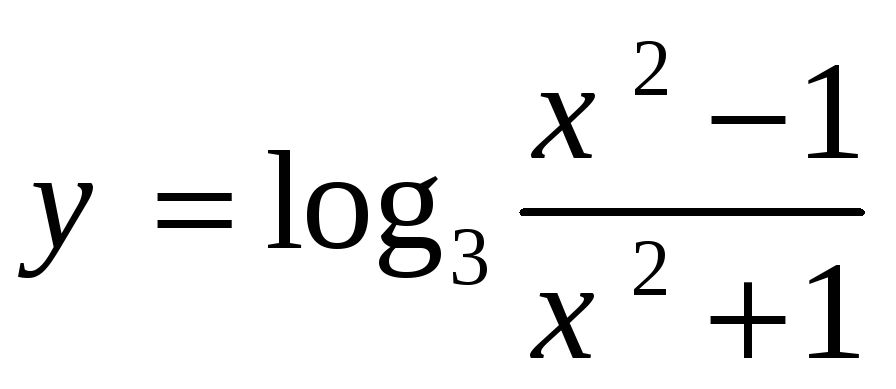
-
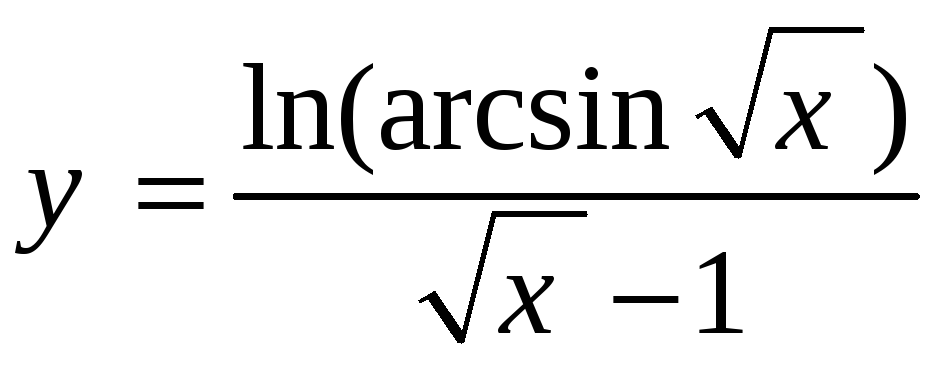
-

-

-

-
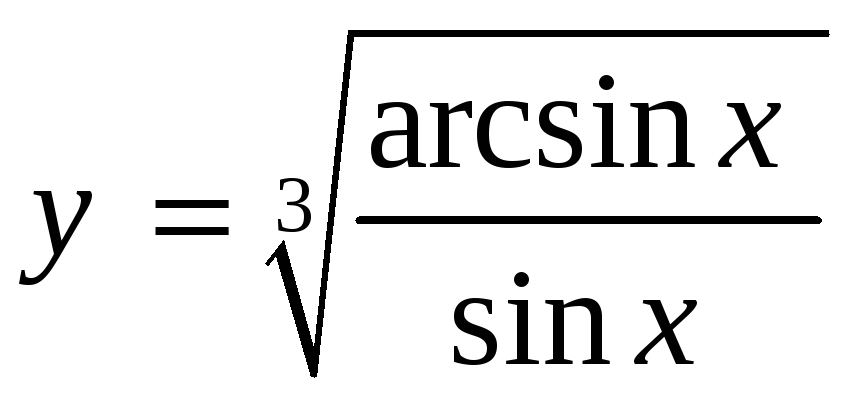
-

-

-

-

-

-

-

-

-

-
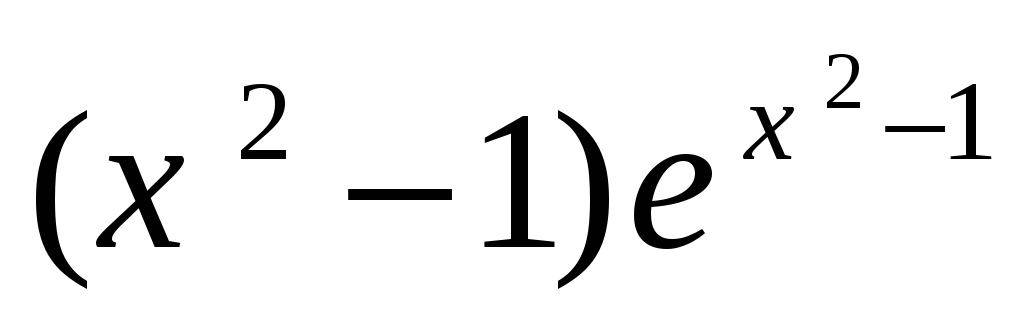
-

-

-

-

-
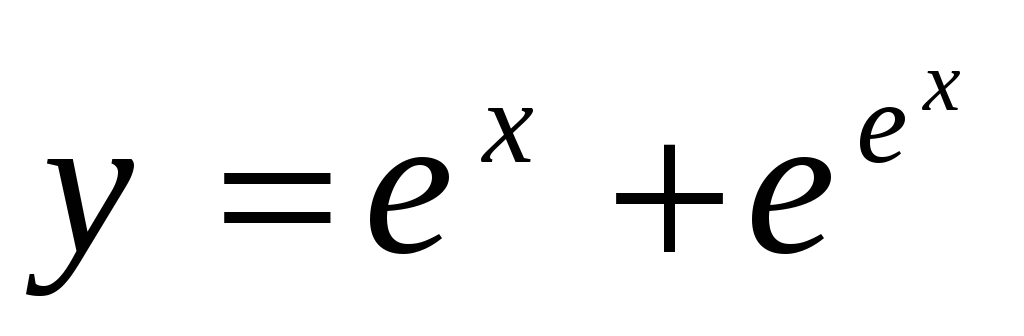
-

-

-

-

-

-

-

-

-
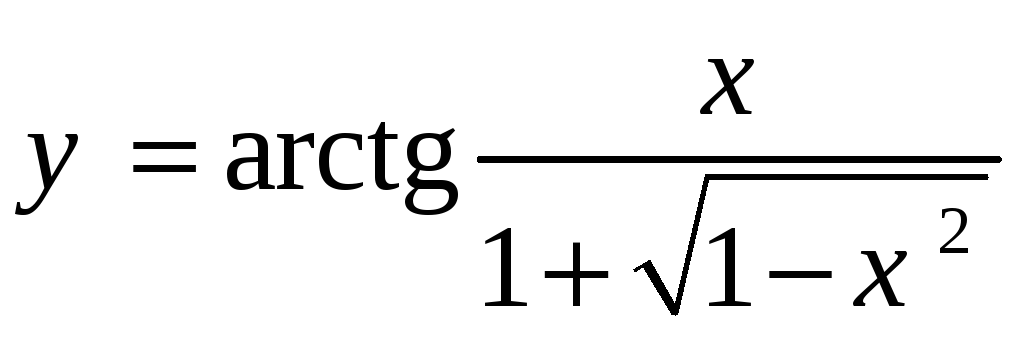
-

-

-
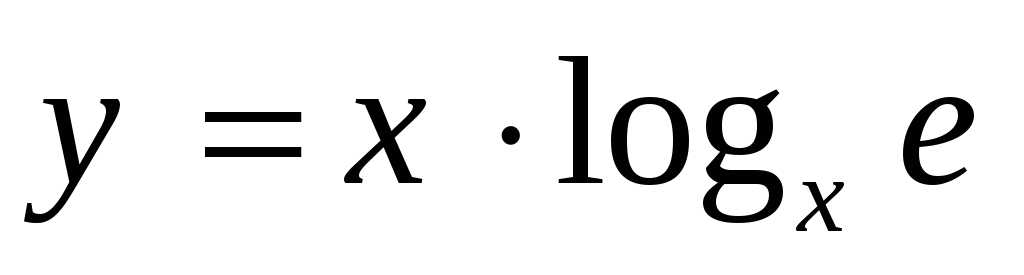
-

-

-

-

-

Пределы.
Матрицы.
-
Решить СЛАУ методом Крамера
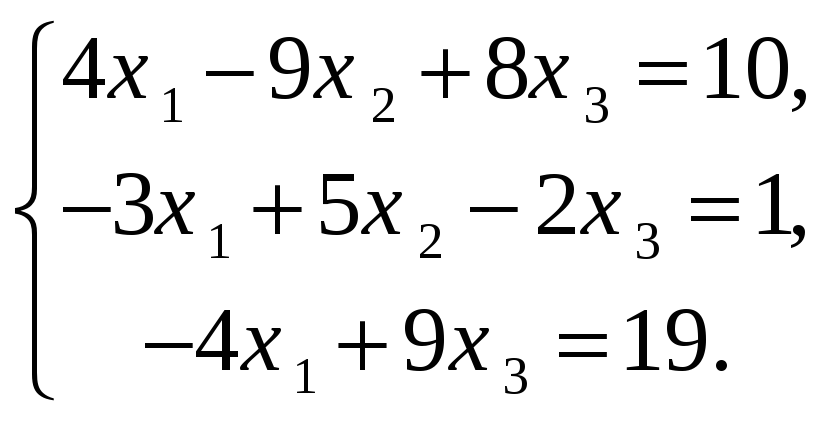




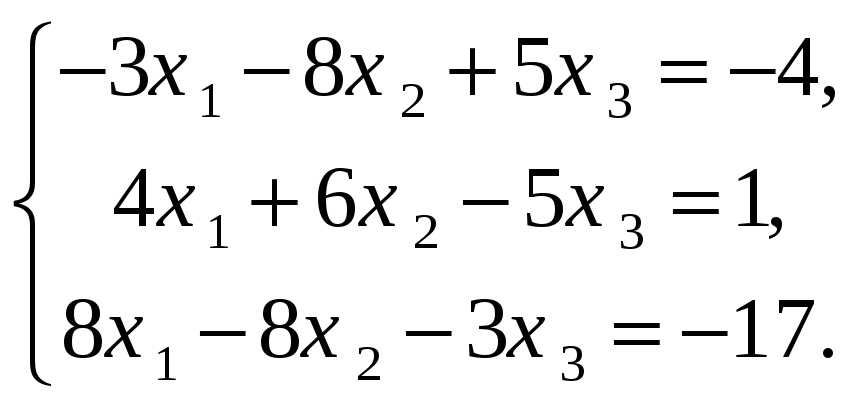


-
Решить СЛАУ методом Гаусса


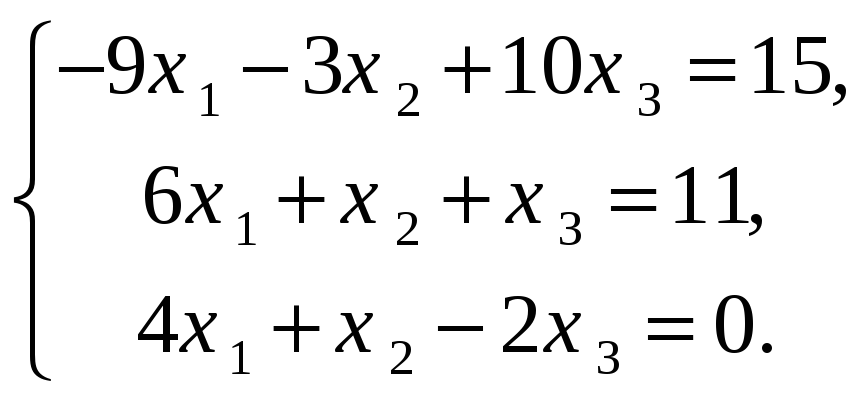
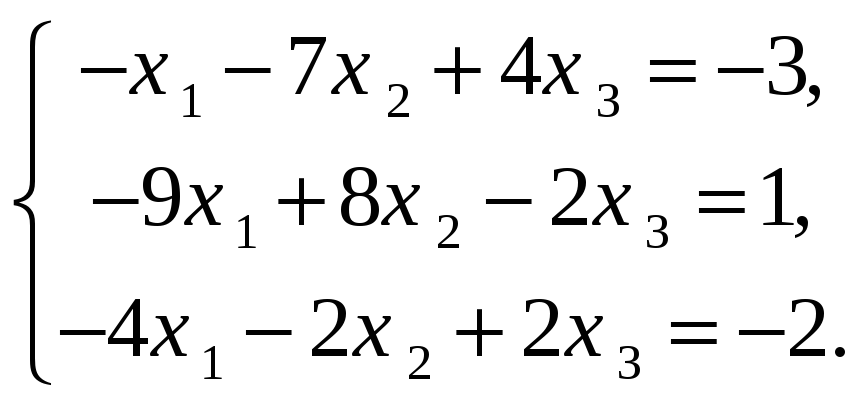

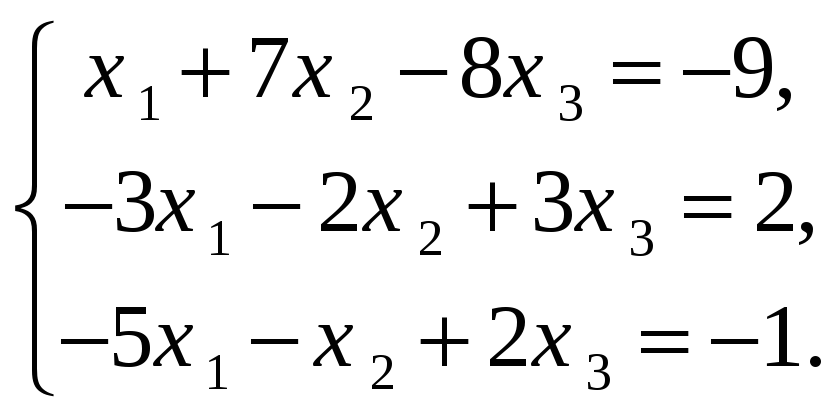


-
Решить СЛАУ методом обратной матрицы
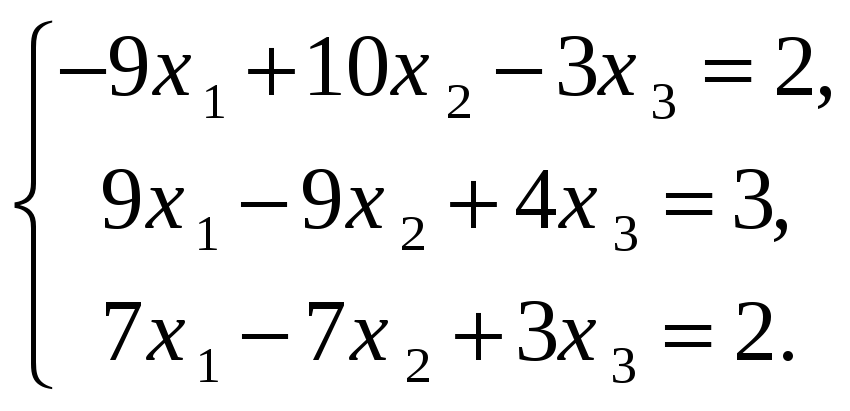


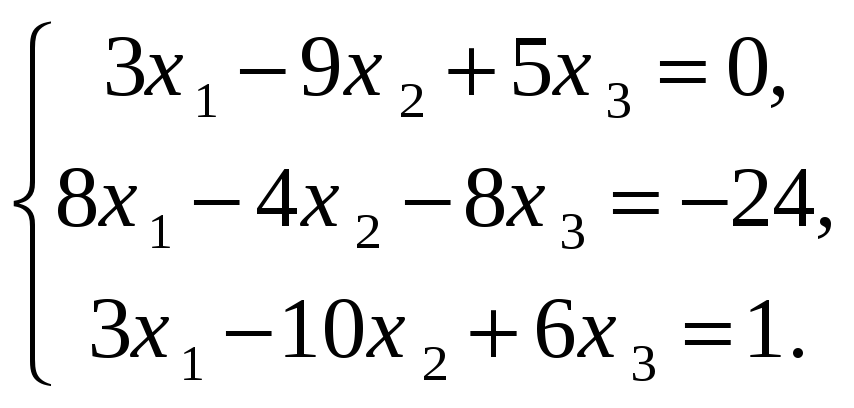




-
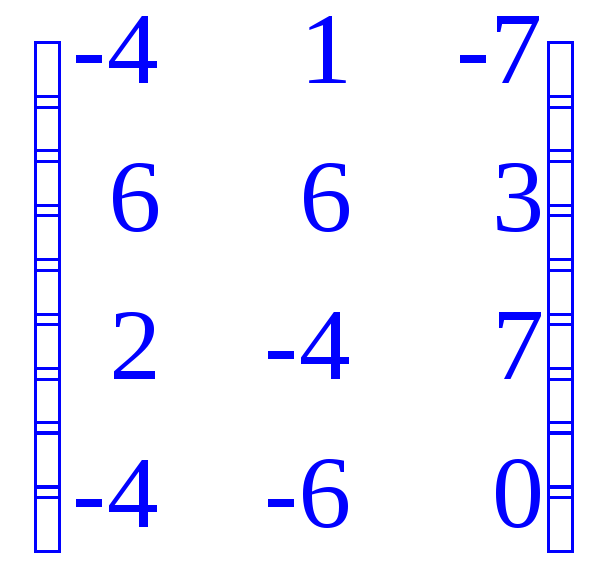
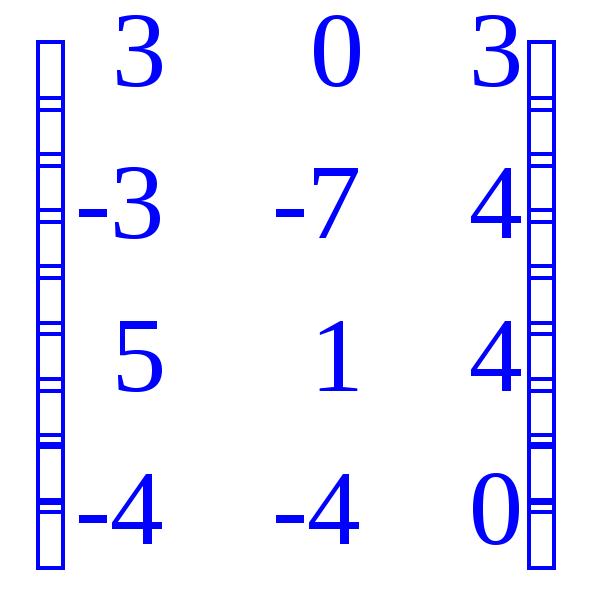
Определить ранг матрицы






Вектора.
-
Для заданных векторов
 ,
,
 ,
,
 найти вектор
найти вектор
 и выразить его в базисе
и выразить его в базисе
 .
(-1,1) *
.
(-1,1) * -
Для заданных векторов
 ,
,
 ,
,
 найти вектор
найти вектор
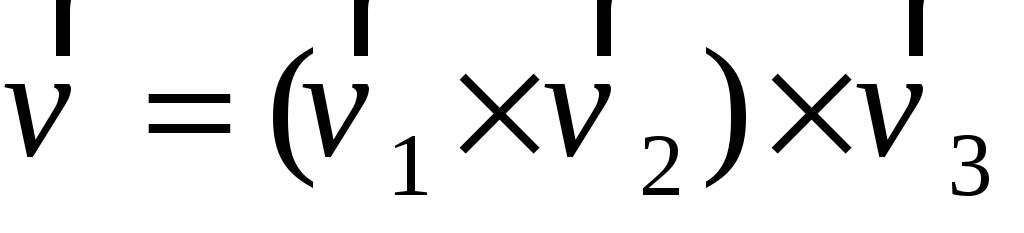 и выразить его в базисе
и выразить его в базисе
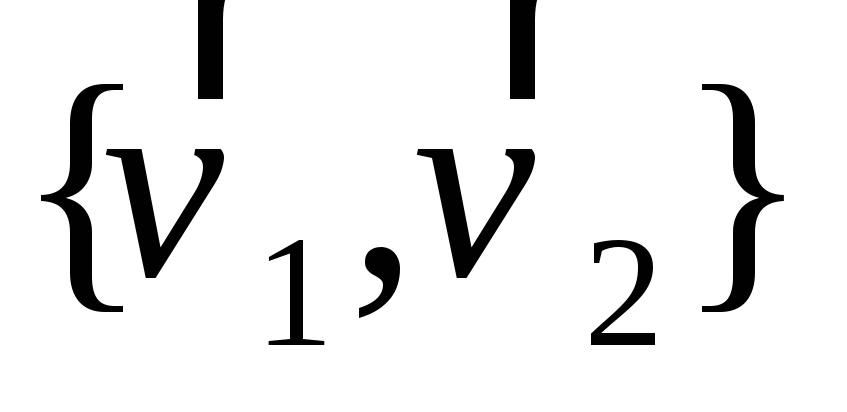 . (1,3)*
. (1,3)* -
Для заданных векторов
 ,
,
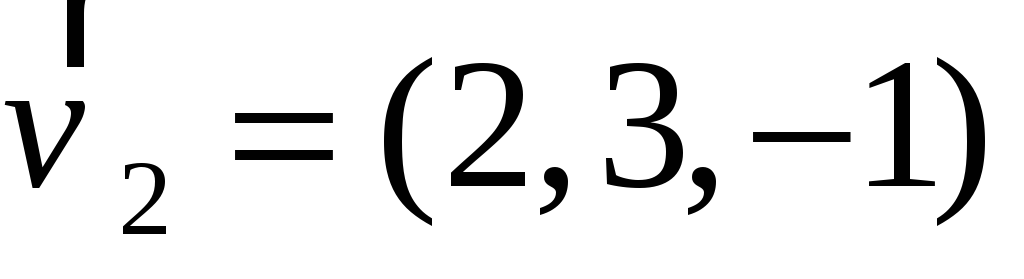 ,
,
 найти вектор
найти вектор
 и выразить его в базисе
и выразить его в базисе
 . (3,5)*
. (3,5)*
-
Найти компланарные векторы среди
 .
.
-
Найти компланарные векторы среди
 .
. -
Найти компланарные векторы среди
 .
.
-
Найти компланарные векторы среди
 .*
.* -
Найти компланарные векторы среди
 .
. -
Найти компланарные векторы среди
 .
. -
Найти компланарные векторы среди
 .*
.* -
Найти компланарные векторы среди
 .
.
-
Найти представление вектора
 в базисе
в базисе
 .
. -
Найти представление вектора
 в базисе
в базисе
 .
. -
Найти представление вектора
 в базисе
в базисе
 .
. -
Найти представление вектора
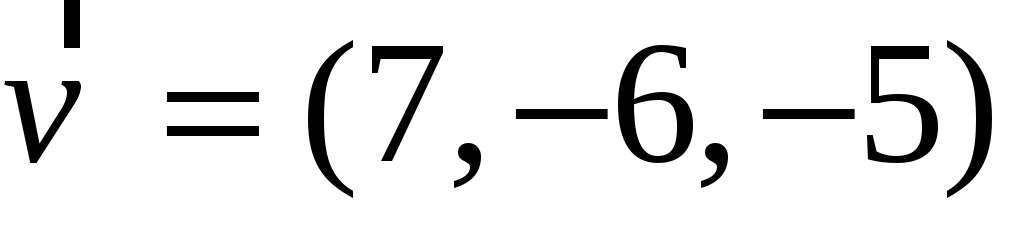 в базисе
в базисе
 .
.
Функции.
-
Определить экстремумы функции и их тип.
-
Определить
 и их тип. *
и их тип. * -
Определить экстремумы функции
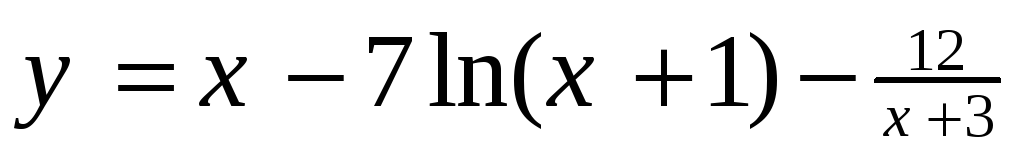 и их тип. *
и их тип. * -
Определить экстремумы функции
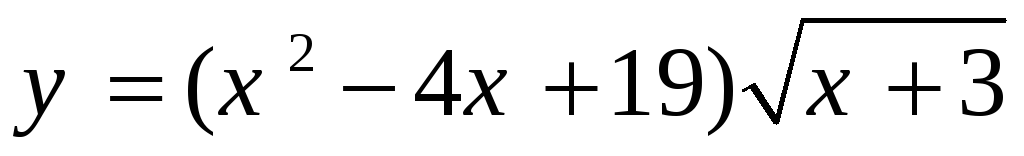 и их тип. *
и их тип. * -
Определить экстремумы функции
 и их тип. **
и их тип. ** -
Определить экстремумы функции
 и их тип. *
и их тип. * -
Определить экстремумы функции
 и их тип. *
и их тип. * -
Определить экстремумы функции
 и их тип. *
и их тип. * -
Определить экстремумы функции
 и их тип. *
и их тип. *
-
-
Определить экстремумы функции и промежутки выпуклости функции.
-
 .
вторая производная
.
вторая производная

-
 .
вторая производная
.
вторая производная

-
 .
вторая производная
.
вторая производная
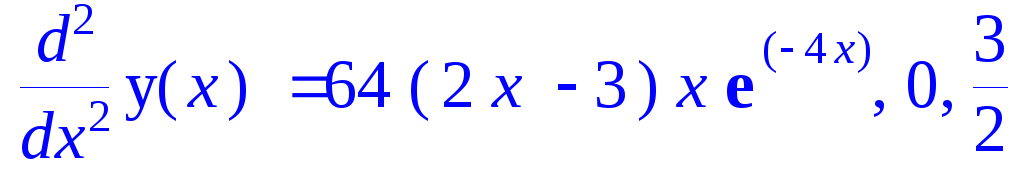
-
Найти асимптоты функции.
-
Найти асимптоты функции
 .
*
.
*
-
асимптота
![]()
-
Найти асимптоты функции
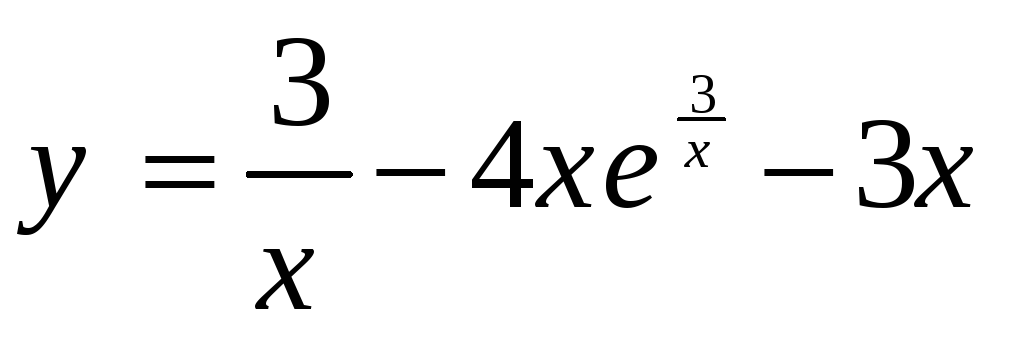 .
*
.
*
асимптота
![]()
-
Найти асимптоты функции
 .
*
.
*
асимптота
![]()
-
Найти асимптоты функции
 .
*
.
*
асимптота
![]()
-
Найти асимптоты функции
 .
*
.
*
асимптота
![]()
-
Найти асимптоты функции
 .
*
.
*
асимптота
![]()
-
Найти асимптоты функции
 .
*
.
*
асимптота
![]()
-
Вычислить приближенно с помощью дифференциала
 .
*
.
* -
Вычислить приближенно с помощью дифференциала
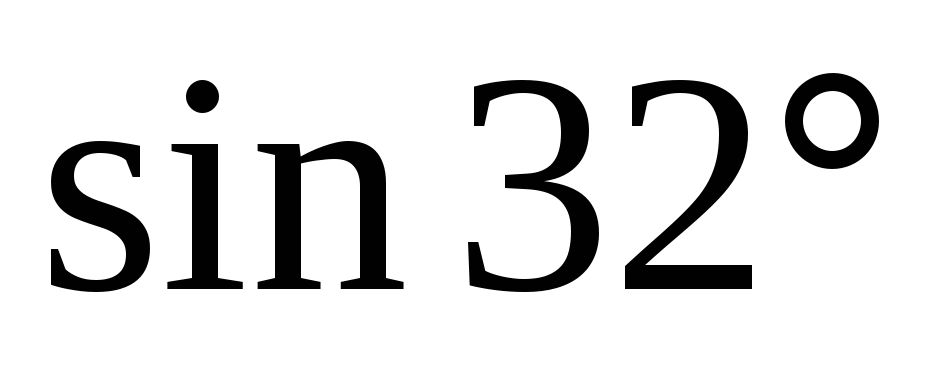 .
*
.
* -
Вычислить приближенно с помощью дифференциала
 .
*
.
* -
Вычислить приближенно с помощью дифференциала
 .
.
-
Аналитическая геометрия
-
Определить проекции на координатные оси перпендикуляра к прямой
 ,
опущенного из начала координат. (45, 60)
*
,
опущенного из начала координат. (45, 60)
* -
Определить проекции на координатные оси перпендикуляра к прямой
 ,
опущенного из начала координат. (70,
168) *
,
опущенного из начала координат. (70,
168) * -
Определить проекции на координатные оси перпендикуляра к прямой
 ,
опущенного из начала координат. (60, 45)
*
,
опущенного из начала координат. (60, 45)
* -
Определить проекции на координатные оси перпендикуляра к прямой
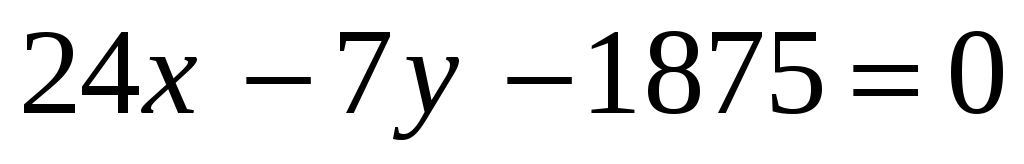 ,
опущенного из начала координат. (72, 21)
*
,
опущенного из начала координат. (72, 21)
* -
Определить проекции на координатные оси перпендикуляра к прямой
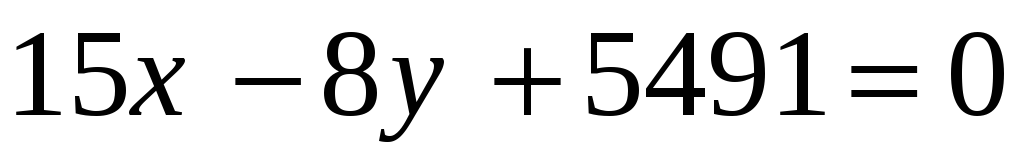 ,
опущенного из начала координат. (285,
152) *
,
опущенного из начала координат. (285,
152) *



