§1.4. Скорость

Следующая кинематическая характеристика движения – скорость – выражает быстроту изменения п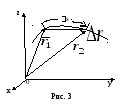оложения тела в пространстве. Изменение положения в пространстве материальной точки характеризуют вектором перемещения:

(1.4.1)

Путь s – это расстояние, пройденное телом по траектории, по определению положительная величина (рис.3). При движении по прямолинейной траектории в одном направлении модуль вектора веремещения и пройденный путь равны друг другу: = s. При движении по криволинейной траектории, а также при изменении направления движения по траектории любой формы< s. Вектор средней скорости за промежуток времени t = t₂ – t₁

<>= (1.4.2)

Направление вектора средней скорости совпадает с направдением вектора перемещения. Из рис.3 видно, что если рассматриваемый участок пути разделить на два одинаковых, то на каждом из них векторы средних скоростей будут различаться, так что <> - довольно грубая характеристика движения. Для получения более точной характеристики надо рассматривать маленькие участки траектории, которым соответствуют маленькие промежутки времени. Предел выражения (1.4.2) при стремлении промежутка времени t к нулю дает мгновенную скорость. В математике такую операцию называют нахождением производной, так что по определению вектор мгновенной скорости

(1.4.3)

Направлен по касательной к траектории, так что ему можно придать вид:

(1.4.4)

где υ– модуль скорости,- касательный орт, т.е. единичный вектор, направленный по касательной к траектории.

На практике зачастую интерес представляет только численное значение скорости. Его легко найти, зная закон движения в скалярной форме (1.3.3):

υ = (1.4.5)

При движении тела по траектории в положительном направлении скорость будет выражаться положительным числом, и, соответственно, отрицательным при движении в отрицательном направлении.

Когда закон движения задан в координатной форме (1.3.2), то проекции вектора скорости на координатные оси есть первые производные по времени от соответствующих координат:

υ_x=,υ _y=,υ _z=, (1.4.6)

соответственно, модуль вектора скорости:

υ= (1.4.7)

При вращении тела путь  равен угловому перемещению. Его измеряют разностью угловых координат в конечныйt₂ и начальный t₁ моменты времени: = ₂ - ₁. Малые угловые перемещения (2) можно считать векторами², будем их обозначать. Этот вектор направлен вдоль оси в соответствии с правилом правого винта, т.е. указывает направление вращения тела, и не имеет фиксированной точки закрепления. Подобные векторы называют аксиальным (осевым) в отличие от полярных векторов, например,или ∆. Быстроту вращения характеризуетугловая скорость. Средняя угловая скорость

<>= /t (1.4.8)

Мгновенная угловая скорость

,(1.4.9)