§2.5. Момент силы.

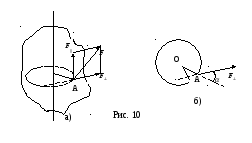Тело (рис.10) может вращаться вокруг неподвижной оси, изображенной вертикальной линией. В точке А к телу приложена сила. При его вращении точка А описывает окружность радиусомr. Разложим силу на две составляющие: одна параллельна оси вращения -F_||,^⁴а другая лежит в плоскости, перпендикулярной оси вращения -F_┴. Очевидно, чтоF_||не может вращать тело. СоставляющаяF_┴лежит в плоскости траектории, описываемой точкой А (рис. 10-б), и образует угол с направлением радиуса окружности. Понятно, что если=0, т.е. линия действияF_┴пересекает ось вращения, то такая сила не вызывает вращения тела. Итак, воздействие на вращающееся тело определяется не только силой, но и тем, где и как она приложена. Эта количественная характеристика воздействия называется моментом силы. По определению момент силы относительно оси вычисляют так:

M = F_d (2.5.1)

d– длина перпендикуляра, опущенного из оси вращения (точка О) на линию действия силыF_, называется плечом силы. На рис.10 б) этот перпендикуляр нарисован, но не обозначен, его длинаd=rsinα, гдеr –расстояние ОА. Единица измерения момента силы в СИ называется ньютон-метр и обозначается Н^.м. Вектор момента силы относительно осинаправлен вдоль оси вращения в соответствии с правилом правого винта, на рис. 10 а) вверх по оси.

§2.6. Уравнение динамики (основной закон динамики)

Общее понятие уравнения динамики мы рассмотрели в §2.1. Оно устанавливает связь между внешним воздействием на тело и изменением состояния тела. Иногда уравнение движения называют основным законом динамики. Обсудим конкретный вид уравнения динамики для двух моделей: м.т. и а.т.т.

Для материальной точкиилидля поступательно движущегося телауравнением движения является второй закон Ньютона:

(2.6.1)

Это дифференциальное уравнение второго порядка, так как . Если известны все действующие на тело силы, а также начальное состояние тела, а именно начальная скоростьи начальное положение, то решение уравнения (2.6.1) определяет состояние тела в любой момент времени:

Отметим, что эту задачу для равнопеременного движения, когда на тело действуют постоянные силы, мы уже решили в §1.6 (смотрите формулы 1.6.2 и 1.6.3)

Уравнению динамики можно придать другой вид, используя понятие импульса :

(2.6.2)

Здесь - равнодействующая всех сил (см. формулу 2.3.6). В частности, для прямолинейного движения под действием постоянной силы это уравнение дает формулу:

∆p=mυ₂-mυ₁=F∆t (2.6.3)

Напомним, что F∆t – называют импульсом силы.

При вращении твердого тела уравнение движениясвязывает между собой соответствующие характеристики вращательного движения:

(2.6.4)

или в другой форме:

(2.6.5)

Здесь - момент импульса тела,- равнодействующая моментов всех сил, действующих на тело.

§2.7. Итоги главы 2. Примеры

Проследим аналогию динамических характеристик и формул поступательного и вращательного движений.

Характеристика, формула	Вид движения
	Поступательное	Вращательное
Состояние	,или ,	φ,или φ,
Мера инертности	т – масса, кг	I - момент инерции, кг^.,м² При вращении вокруг оси симметрии момент инерции: а) обруч, тонкостенный цилиндр: I₀ = m R²- б) диск, сплошной цилиндр: в) шар:
Мера воздействия	- сила, Н F_тяж= mg - сила тяжести F_упр = - kx – сила упругости F=µN – сила трения	- момент силы, Н^.м M = F_d –момент силы относительно оси, F_- проекция силы на перпендикулярную оси вращения плоскость, d – ее плечо
Уравнение движения	или , где - импульс	или , где - момент импульса тела