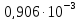3. Расчёт балки на прочность и жёсткость при плоском поперечном изгибе

Дано:

1. расчётная схема балки (РГР-1, задача 3);

2. эпюры поперечных сил и изгибающих моментов, построенные в РГР-1 задача 3;

3. допускаемые нормальные [σ] и касательные напряжения [τ] для материала балки [σ] = 160 МПа, [τ]=100 МПа;

4. модуль продольной упругости материала балки Е=2∙10⁵ МПа;

5. допускаемый прогиб балки и [у]=l_к:200=0,015 м – для консольной балки длиной l_к.

Требуется:

1. из условия прочности определить размеры прямоугольного поперечного сечения балки при h/b=2 (h и b – соответственно высота и ширина сечения);

2. подобрать по сортаменту прокатной стали номер двутавра, удовлетворяющий условию прочности;

3. сравнить по весу балки прямоугольного и двутаврового поперечных сечений и оценить экономию материала при изготовлении двутавровой балки;

4. для каждой из балок построить эпюры распределения нормальных напряжений σ по высоте опасного сечения, где М_х=|М_{х max}|;

5. для каждой из балок построить эпюры распределения касательные напряжений τ по высоте опасного сечения, в котором Q_x=|Q_{x max}|;

6. проверить прочность балок по касательным напряжениям;

7. построить эпюры углов поворота θ и прогибов y для двутавровой балки;

8. проверить двутавровую балку на жесткость;

9. если условие жесткости y ≤ [y], не выполняется, определить новый двутавр, для которого условие y ≤ [y ] будет выполнено.

Рис. 3. Расчетная схема балки с эпюрами поперечных сил, изгибающих моментов, углов поворота и прогибов.

Решение:

1. Определение размеров прямоугольного поперечного сечения балки. Из эпюры М_х определяется максимальное значение изгибающего момента M_{х max}. Из условия прочности при изгибе (3.1):

(3.1)

где σ – максимальное по абсолютной величине расчётное нормальное напряжение в опасном сечении; M_{х max} – максимальный по абсолютной величине изгибающий момент (рис. 3); W_н.о. – момент сопротивления поперечного сечения балки относительно нейтральной оси; [σ] – допускаемое нормальное напряжение материала балки.

Определяем требуемый момент сопротивления:

Так как для прямоугольника момент сопротивления определяется формулой (3.2):

(3.2)

то с учётом зависимости отношения h=2b, можно выразить значение требуемой ширины сечения балки:

После округления до стандартного значения, ширина равняется: b=60 мм, из соотношения h=2b определяем высоту сечения h=2∙60=120 мм, площадь сечения соответственно равна А_ст=b∙h=0,06∙0,12=0,0072 м².

По принятым значениям ширины и высоты сечения балки определяем уточнённое значение момента сопротивления:

Для двутавровой балки:

Выбор номера двутавра делается из сортамента и зависит от значения W_н.о.тр (требуется выбрать такой двутавр, который бы удовлетворял условию прочности).

Принимаем W_z=W_н.о.ст=184 см³, как самое близкое к значению W_н.о.тр и удовлетворяет условию прочности. Номер выбранного двутавра из сортамента прокатной стали 20.

Проверка условий прочности балки по касательным напряжениям

Данные из каталога для двутавра №20:

1. Размеры

h_ст= 200 мм; b_ст= 100 мм; s=5,2 мм; t=8,4 мм;

2. площадь сечения S_сеч=26,8 см²

3. справочные величины для оси Z

I_z=I_н.о.ст= 1840 см⁴- момент инерции поперечного сечения двутавра

W_z=184 см³- момент сопротивления материала двутавра

S_z=104 см³- статистический момент двутавра.

Для определения достоинства выбранной двутавровой балки по сравнению с балкой прямоугольного сечения сравним их по весу.

2. Для этого посчитаем коэффициент экономичности:

где S_сеч – площадь поперечного сечения двутавра (принимается из таблицы значений для двутавровых балок); S_пр=b∙h – площадь прямоугольного сечения балки.

По значению коэффициента Э видно, что в случае использования балки двутаврового сечения имеет место экономия, тем самым становится очевидным использование балки двутаврового сечения.

3. Построение эпюр распределения нормальных напряжений σ по высоте опасного сечения балки прямоугольного сечения и двутавровой балки. Распределение напряжений в опасном сечении при изгибе можно рассчитать по формуле (3.3):

(3.3)

где у – расстояние от рассматриваемой точки до нейтральной оси сечения; I_н.о. - момент инерции поперечного сечения балки относительно нейтральной оси.

Для балки прямоугольного сечения

Для двутавра:

4. Построение эпюр распределения касательных напряжений для прямоугольного и двутаврового сечений:

Балка прямоугольного сечения:

По эпюре сил Q_х определяется максимальное по абсолютной величине значение Q_{x max}

Распределение напряжений τ в прямоугольном сечении подчиняется закону (3.4):

(3.4)

Двутавровая балка:

Напряжения τ в отдельных слоях сечения определяются по правилу Журавского 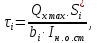(3.5):

(3.5)

где – ширина рассматриваемого слоя i;- статический момент относительно нейтральной оси части сечения, расположенной по одну сторону от рассматриваемого слояi.Всего рассматривается семь слоёв:

b₁= b₂= b₆= b₇= b_ст; b₃= b₄= b₅= S; S₁^*= S₇^*=0;

Для слоёв 2, 3, 5, 6 моменты определяются по формуле:

S₂^*= S₃^*= S₅^*= S₆^*=

S₄^*= S_z^*=0,104м³;

5. <100 МПа – условие жёсткости выполняется

6. Построение эпюры углов поворота ϴ и прогибов y для двутавровой балки.

Е=2МПа; двутавр №20

I_н.о.ст=1840 см⁴ =1840 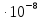м⁴;

Е∙I_н.о.ст=21840=3,68кН∙ м²;

По формуле (3.6) определяем углы поворота сечений:

(3.6)

где – моментный угол поворота крайнего справа сечения на (i-1) участке;- момент инерции поперечного сеченияi-ого участка балки относительно нейтральной оси; – изгибающий момент и поперечная сила в началеi-ого участка, по эпюрам M_x и Q_x; х_i – расстояние рассматриваемого сечения от левого конца i-ого участка; 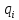- распределённая нагрузка наi-ом участке.

Определяем углы поворота сечений:

1. для первого грузового участка 0≤х₁≤2:

При х₁=0,

При х₁=0,5,

При х₁=1,

При х₁=2,

2. для второго грузового участка 0≤х₂≤1:

При х₂=0,

При х₁=0,5,

При х₂=1,

7. Определим прогибы y_{i M} по формуле (3.7):

(3.7)

где моментный прогиб крайнего справа сечения на i-1 участке. Для первого грузового участка равен 0.

1. первый грузовой участок 0≤х₁≤2:

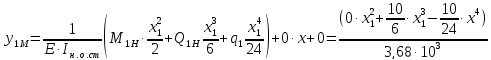
При х₁=0,

При х₁=0,5,

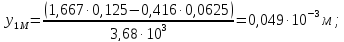
При х₁=1,

При х₁=2,

2. второй грузовой участок 0≤х₂≤1:

При х₂=0,

При х₁=0,5,

При х₂=1,

8. Расчёт начальных параметров для балки с жесткой заделкой на правом конце по формулам (3.8), (3.9):

(3.8) (3.9)

где – моментный угол поворота сечения в заделке;длина балки;– моментный прогиб сечения в опоре Б.

9. Находим полные перемещения сечений балки ϴ и у по формулам (3.10) и (3.11) соответственно:

; (3.10) , (3.11)

где х – расстояние от левого конца балки до рассматриваемого сечения; и– угол поворота и прогиб для рассматриваемого сечения х;– начальный параметр.

При х=0,5 ϴ=-= –5,603∙10^-3 рад;

у=м

При х=1 ϴ=-= –4,980∙10^-3 рад;

у=

При х=2 ϴ5,886= –4,076∙10^-3 рад;

у=

При х=2,5 ϴ5,886= –1,698∙10^-3 рад;

у=

При х=3 ϴ=-0 рад;

у=

Х, м	ϴм, рад	ϴ, рад	Ум, см	У, см
0	0		0	1,1773
0,5		–5,603∙10-3	0,0049	0,8939
1		-4,980∙10-3	0,0340	0,6227
2		-4,076∙10-3	0,1811	0,1812
2,5	4,188	–1,698∙10-3	0,3338	0,0396
3		0	0,5885	0