Аналитическа геометрия

3

3

C

2

2

X

2C

C

2

.

C

1

Если национальный доход третьей страны равен 200 денежным

единицам, т. е x

200 ,

то x

400 ,

а x

3

200 300 .

2

3

2

1

Решение задачи 2.

Две точки

A( 3;2) и B( 1;1)

лежат на прямой, следовательно вектор

2 ,

т.е.

2; 1 ,

лежит на прямой и является

a AB 1 3;1

a

направляющим вектором этой прямой. Используем уравнение (5)

x x0

y y0

,

l

m

M0 x0

, y0 -

где a l;m 2; 1 , а

точка лежащая на прямой. В качестве

такой точки можно взять, например, точку A( 3;2) . Тогда уравнение прямой

имеет вид

x 3

y 2

.

2

1

d

Ax1 By1 Cz1 D

1 ( 2) 2 ( 1) ( 2) ( 3) 4

2

2

.

3

3

A2 B2 C 2

12 22 ( 2)2

задачи, искомая

прямая

перпендикулярна

плоскости, следовательно,

нормальный вектор плоскости n параллелен прямой и его можно взять за

направляющий вектор a прямой. Итак,

a

n 5; 2;3 .

Используем

канонические

уравнения

прямой (18), подставив

координаты точки M0 3,1, 4 и координаты вектора a 5; 2;3 . Получим:

x 3

y 1

z 4

.

5

2

3

2

1

0

3

3

A

1

2

5

.

9

9

9

2

4

4

9

9

9

M2 2;3;2 и M3 3;3;1 .

4. Написать уравнение прямой, проходящей через точку M0 2; 5;6 и

параллельной прямой

x 1

y 3

z

.

4

3

1

Составим матрицу A E

и приведем еѐ к ступенчатому виду.

2

1

1

1

1

0

0

1

0

3

3

3

3

1

A E

1

2

1

5

1

7

5

7

~

1

5

~

9

9

9

9

9

9

2

4

4

1

2

4

5

2

4 5

9

9

9

9

9

9

(первую строку умножили на 3, вторую и третью – на 9)

1

1

0

1 1

0

1 1

0

1 1

1 0

1

1 0

0

0

6 5

~

0 6

5

~

~

1

7

1 5

0

6 5

0 6 5

0 0

0

1 1

1 0

0

2

4

2

5

5

5

C

6

6

5

5

X

C

C

.

6

6

C

1

Если национальный доход третьей страны равен 600 денежным

единицам, т. е

x 600

, то

x

5

600 500 и

x

x

500

денежных

3

2

6

1

2

d

Ax0 By0 C

4 6 3 ( 1) 31

24 3 31

10

10

2 .

5

5

A2 B2

42 32

25

x 1

y 2

z 1

x 1

y 2

z 1

2 1

3 2

2 1

1

1

3

3 1

3 2

1 1

2

1

2

3

1 3

1 1

(x 1)

1

( y 2)

(z 1)

(x 1) 4( y 2) (z 1)

1

2

2

2

2

1

x 1 4y 8 z 1 x 4y z 8.

Уравнение плоскости имеет вид: x 4y z 8 0 .

Решение задачи 4.

Будем искать уравнение прямой в виде (18). Поскольку искомая прямая

параллельна

данной,

то

их

направляющие

векторы совпадают т .е.

3; 4;1 . Искомая прямая проходит через точку M0 2; 5;6 . Подставляя эти

a

данные в уравнения (18), получаем уравнения искомой прямой:

x 2

y 5

z 6

.

4

3

1

1

1

1

4

2

4

A

1

1

3

.

8

4

8

5

1

3

8

4

8

2. Написать уравнение

прямой, проходящей через точку M0 3;10

перпендикулярно прямой

x 2

y 1

.

6

7

14

перпендикулярно прямой

x 1

y 4

z 1

.

1

2

3

4. Вычислить косинус угла между прямыми

x

2 t,

x 5

z 1

y

y 1 3t,

и

.

2

1

3

4 2t

z

Решение задачи 1.

Вектор-столбец национальных

доходов,

обеспечивающих бездефицитную

Составим матрицу A E

и приведем еѐ к ступенчатому виду.

1

1

1

1

3

1

1

3 2 1

4

2

4

4

2

4

A E

1

1

1

3

1

3

3

6 3

~

1

~

8

4

8

8

4

8

2 5

5

1

3

1

5

1

5

5

8

4

8

8

4

8

6

1

3

1 6

3

1

6

3

1

6

3

1

6

1 3

~

3 2

1

~

0

3 2

3

1

0

16

10

~

0

8

5

~

5 2

5

0 32

20

0 8

5

6

1 3

1

0

5

5

2

5

1

6

3

~

0

8

5

1

- 6

3

~

.

0

8

5

0

0

0

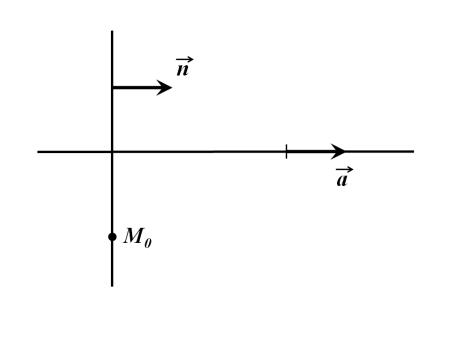
8x 5x 0 x

5

x .

2

3

2

8

3

Если

x C ,

то

x

5

C .

Первая

строка означает

уравнение

3

2

8

x 6x

3x 0

. Подставив x

C

и x

5

C , получим x

3

C .

1

2

3

3

2

8

1

4

Таким

образом,

вектор-столбец

национальных

доходов

стран,

обеспечивающий бездефицитную торговлю имеет вид

3

3

C

4

4

5

5

X

C

C

.

8

8

C

1

Если национальный доход третьей страны равен 80 денежным

единицам, т. е x

80

, то

x

5 80 50 , а

x

3

80 60

денежных единиц.

3

2

8

1

4

Решение задачи 2.

Будем искать уравнение прямой перпендикулярной данной в виде (3).

A; B - вектор перпендикулярный данной в условиях задачи прямой,

Т.к. n

которая

задана

каноническим

уравнением

вида (5),

то n a ,

где a -

6; 7 .

Прямая проходит через точку M0 3;10 .

Тогда

n

a

Подставляя

эти

данные в

уравнение (3), получим 6(x 3) 7( y 10) 0 .

нормальный вектор

параллелен направляющему вектору

прямой.

n

a

Можно взять n

a (см. рис. 4).

Рисунок 4. Чертеж к задаче 3 варианта № 3.

M0 3; 1;12 .

Итак,

n a 1;2;3 . Плоскость

проходит через точку

Подставляя эти данные в уравнение (9), получим

(x 3) 2( y 1) 3(z 12) 0 .

Упрощая, получаем: x 2y 3z 31 0 .

Решение задачи 4.

Направляющие векторы прямых, заданных в условии задачи, равны

a1

1;3;2 и a2 2;1;3 . Воспользуемся формулой (19):

l1l2 m1m2 n1n2

( 1)( 2) 3 1 2 3

11

cos

.

14

2

2

2

2

2

2

( 1)

2

3

2

2

2

( 2)

2

2

3

2

l1

m1

n1

l2

m2

n2

1

1

1

1

3

4

2

A

1

1

1

.

x 3

y

x 6 4t,

и

3t.

5 12

y 9

1

1

1

2

3

4

A

1

1

1

.

4

3

4

1

1

1

3

2

4

1

1

1

2

5

4

A

1

3

0

.

4

5

1

1

3