L04-EM

05.04.2012

21 Контур с током

• Силы f и f ' образуют пару, момент которой равен

Mfb iBab

•Учитывая, что ab равно площади контура S, а iS

дает величину магнитного момента pm, можно написать

•Момент М стремиться повернуть контур так, чтобы

его магнитрый момент pm установился по

направлению поля В. Такая ориентация контура показана на рис. 88.

22 Контур с током

• В этом случае f1 = f3 = iBa, f2 = f4 = iBb

11

05.04.2012

23 Контур с током

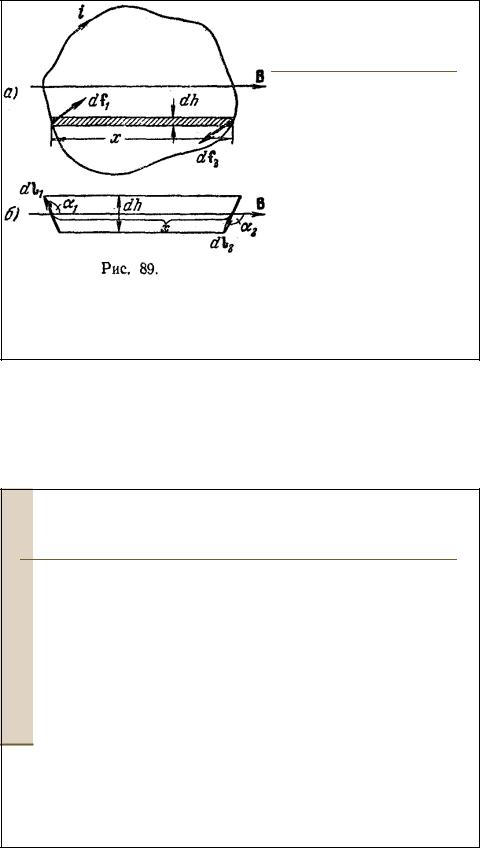
24 Контур с током

•Силы df1 и df2 одинаковы по величине и образуют пару, момент которой равен

dM iBdh b

•где b – длина полоски. Произведение bdh дает

площадь полоски dS. Таким образом,

dM iBdS

•Беря попарно силы, приложенные к противо-

лежащим элементам контура, и суммируя их моменты, получим результирующий момент,

действующий на контур:

M dM iB dS iSB pm B

12

05.04.2012

25Контур с током

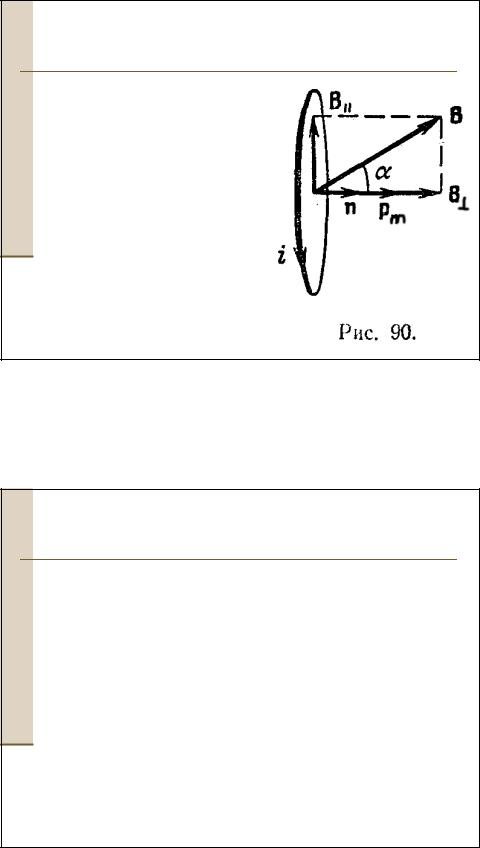
•Составляющая В будет

растягиват или сжимать

контур. Составляющая В║,

величина которой равна

Bsinα (α – угол между pm и B), приведет к возникновению вращательного

момента, который можно

вычислить по формуле:

26Контур с током

•Для того чтобы угол α между векторами pm и B

увеличить на dα, нужно совершить против сил, действующих на контур в поле, работу

•Работа (2.157) идет на увеличение энергии W, которой

обладает контур с током в магнитном поле

dW pm B sin d

W pm B cos const

13

05.04.2012

27Контур с током

•Рассмотрим плоский контур с током в неоднородном

магнитном поле. Предположим, что поле изменяется быстрее всего в направлении х (рис. 91, а)

28Контур с током

•С помощью выражения (2.158) для энергии контура можно найти выражение для f. Дифференцируя W по х и изменяя знак, получим проекцию силы на ось х.

•Если векторы pm и B совпадают по направлению, сила

положительна, т. е. направлена в сторону возрастания B. Если они антипараллельны, то сила отрицательна, т. е. направлена в сторону убывания B

14