
Глава 1. Расчётная часть
1.1 Материальный баланс
Для начала, сравнивая температуры кипения компонентов бинарной системы ацетон – метиловый спирт, определим, какой из компонентов является легколетучим, а какой труднолетучим. Температура кипения ацетона при 1 атм 56,4оС, температура кипения метилового спирта при 1 атм 64,8оС, следовательно, легколетучим компонентом в данной бинарной смеси является ацетон. [5, с. 3]
Обозначим
массовый расход исходной смеси
 ,
массовый расход дистиллята
,
массовый расход дистиллята
 ,
массовый расход кубового остатка
,
массовый расход кубового остатка ,
концентрацию легколетучего компонента
в исходной смеси в массовых долях
,
концентрацию легколетучего компонента
в исходной смеси в массовых долях ,
концентрацию легколетучего компонента
в дистилляте в массовых долях
,
концентрацию легколетучего компонента
в дистилляте в массовых долях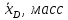 ,
концентрацию легколетучего компонента
в кубовом остатке в массовых долях
,
концентрацию легколетучего компонента
в кубовом остатке в массовых долях .
В задании по курсовому проектированию
массовый расход исходной смеси дан вт/час:
.
В задании по курсовому проектированию
массовый расход исходной смеси дан вт/час:
 .
Сделаем перевод в систему СИ:
.
Сделаем перевод в систему СИ:

Применим уравнения материального баланса [4, с. 11]:
а)
баланс по потокам:
 (1.1.1)
(1.1.1)
б) баланс по содержанию легколетучего компонента в потоке:
 (1.1.2)
(1.1.2)
Составив систему из уравнений материального баланса:

и
подставив в неё известные нам из задания
по курсовому проектированию данные ( ,
, ,
, ,
, ),
найдём массовые расходы дистиллята и
кубового остатка:
),
найдём массовые расходы дистиллята и
кубового остатка:




Для
дальнейших расчётов необходимо выразить
концентрации легколетучего компонента
в исходной смеси
 ,
дистилляте
,
дистилляте и в кубовом остатке
и в кубовом остатке в мольных долях [6, с. 283]:
в мольных долях [6, с. 283]:
 ,
(1.1.3)
,
(1.1.3)
где
 – молярная масса легколетучего компонента
смеси (в нашем случае ацетона,
– молярная масса легколетучего компонента
смеси (в нашем случае ацетона,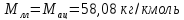 [5, с. 3]);
[5, с. 3]);
 –молярная
масса труднолетучего компонента смеси
(в нашем случае метилового спирта,
–молярная
масса труднолетучего компонента смеси
(в нашем случае метилового спирта,
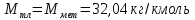 [5, с. 3]).
[5, с. 3]).



Определим
мольную долю ацетона (легколетучего
компонента) в паре
 ,
равновесном с жидкостью питания,
интерполируя значения из таблицы по
равновесию пар – жидкость в бинарной
смеси ацетон – метиловый спирт [2, с. 5]:
,
равновесном с жидкостью питания,
интерполируя значения из таблицы по
равновесию пар – жидкость в бинарной
смеси ацетон – метиловый спирт [2, с. 5]:

Найдём
минимальное число флегмы
 в ректификационной колонне непрерывного
действия [6, с. 321]:
в ректификационной колонне непрерывного
действия [6, с. 321]:
 (1.1.4)
(1.1.4)
Найдём рабочее число флегмы [6, с. 321]:
 (1.1.5)
(1.1.5)
Уравнение рабочей линии верхней части ректификационной колонны [6,с. 320]:
 (1.1.6)
(1.1.6)

Уравнение рабочей линии нижней части колонны [6, с. 320]:
 ,
(1.1.7)
,
(1.1.7)
где
 – относительный мольный расход питания,
определяемый по формуле [6, с. 320]:
– относительный мольный расход питания,
определяемый по формуле [6, с. 320]:
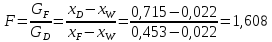 (1.1.8)
(1.1.8)


1.2 Тепловой баланс
Зная мольный состав исходной смеси (жидкости питания), дистиллята и кубового остатка, найдём их температуры кипения, используя данные таблицы равновесия пар – жидкость для бинарной смеси ацетон – метиловый спирт [2, с. 5]:



Найдём
расход теплоты, получаемой кипящей
жидкостью в кубе колонны при конденсации
греющего пара
 [4, с. 23, 25]:
[4, с. 23, 25]:
 (1.2.1)
(1.2.1)
где
 – расход теплоты, отдаваемой охлаждающей
воде в дефлегматоре,
– расход теплоты, отдаваемой охлаждающей
воде в дефлегматоре,
 –теплоёмкости
жидкостей состава
–теплоёмкости
жидкостей состава
 при температурах
при температурах соответственно, которые определяют по
формуле аддитивности [3, с. 4]:
соответственно, которые определяют по
формуле аддитивности [3, с. 4]:
 (1.2.2)
(1.2.2)
где
 и
и – теплоёмкости легколетучего и
труднолетучего компонентов смеси (в
нашем случае ацетона и метилового
спирта) при соответствующих температурах,
определяемые по номограмме [6, с. 562].
– теплоёмкости легколетучего и
труднолетучего компонентов смеси (в
нашем случае ацетона и метилового
спирта) при соответствующих температурах,
определяемые по номограмме [6, с. 562].



Расход теплоты, отдаваемой охлаждающей воде в дефлегматоре, определим по формуле [4, с. 24]:
 ,
(1.2.3)
,
(1.2.3)
где
 – массовый расход дистиллята,
– массовый расход дистиллята,
 –флегмовое
число,
–флегмовое
число,
 –удельная
теплота парообразования дистиллята,
которая рассчитывается по аддитивной
формуле [3, с. 6]:
–удельная
теплота парообразования дистиллята,
которая рассчитывается по аддитивной
формуле [3, с. 6]:
 ,
(1.2.4)
,
(1.2.4)
где
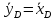 при использовании дефлегматора,
при использовании дефлегматора,
 и
и
 – удельные теплоты парообразования
легколетучего и труднолетучего
компонентов смеси (в нашем случае ацетона
и метилового спирта соответственно)
при температуре кипения дистиллята
– удельные теплоты парообразования
легколетучего и труднолетучего
компонентов смеси (в нашем случае ацетона
и метилового спирта соответственно)
при температуре кипения дистиллята ,
определяемые при интерполяции данных
таблицы удельных теплот парообразования
[5, с. 15]:
,
определяемые при интерполяции данных
таблицы удельных теплот парообразования
[5, с. 15]:
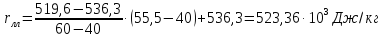


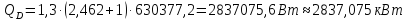
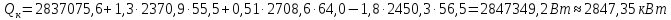
1.3 Расчёт средних физических величин смеси
Для дальнейшего расчёта нам необходимо знать значения некоторых физических величин смеси. Методика их расчёта приведена в литературе [3].
Расчёт ректификационной колонны начинают с определения средних значений температур, теплофизических свойств жидкости и пара, а также их расходов. Этот этап предшествует гидравлическому расчёту колонны. Жидкостные и паровые потоки являются смесями компонентов, свойства которых рассчитываются на основе свойств чистых веществ в зависимости от состава и температуры потока. Для простой полной колонны, обогреваемой горячей водой, средние составы и расходы по жидкости и пару, а также физические величины определяют отдельно для верхней и нижней частей колонны (индексы в и н). Индексу А соответствует легколетучий компонент (ацетон), индексу В труднолетучий компонент (метиловый спирт).
а) Для жидкой фазы в верхней и нижней частях колонны:
– мольные
составы
 и
и определяют как среднеарифметические:
определяют как среднеарифметические:
 ,
(1.3.1)
,
(1.3.1)
 ;
(1.3.2)
;
(1.3.2)
– мольные
массы смеси
 определяют по формуле:
определяют по формуле:
 ,
(1.3.3)
,
(1.3.3)
где
 – мольные массы исходных веществ,
– мольные массы исходных веществ, [5, с. 3];
[5, с. 3];


– массовые
составы
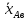 и
и определяют по уравнению
определяют по уравнению
 ,
(1.3.4)
,
(1.3.4)
где
 – мольная масса смеси;
– мольная масса смеси;


– средние
температуры
 определяют, интерполируя данные таблицы
равновесия пар – жидкость бинарной
системы ацетон – метиловый спирт [2, с.
5] при соответствующих значениях
определяют, интерполируя данные таблицы
равновесия пар – жидкость бинарной
системы ацетон – метиловый спирт [2, с.
5] при соответствующих значениях и
и :
:


– плотности
 определяют по уравнению:
определяют по уравнению:
 ,
(1.3.5)
,
(1.3.5)
где
 – плотности легколетучего и труднолетучего
компонентов при соответствующих
температурах,
– плотности легколетучего и труднолетучего
компонентов при соответствующих
температурах, ,
которые находим, интерполируя данные
таблицы плотности жидкостей в зависимости
от температуры [5, с. 4]:
,
которые находим, интерполируя данные
таблицы плотности жидкостей в зависимости
от температуры [5, с. 4]:






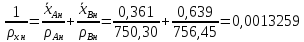
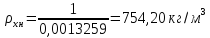
– динамические
коэффициенты вязкости
 рассчитывают по уравнению:
рассчитывают по уравнению:
 ,
(1.3.6)
,
(1.3.6)
где
 – динамические коэффициенты вязкости
легколетучего и труднолетучего
компонентов при соответствующих
температурах,
– динамические коэффициенты вязкости
легколетучего и труднолетучего
компонентов при соответствующих
температурах, ,
которые находим, интерполируя данные
таблицы зависимости динамического
коэффициента вязкости органических
жидкостей от температуры [5, с. 5]:
,
которые находим, интерполируя данные
таблицы зависимости динамического
коэффициента вязкости органических
жидкостей от температуры [5, с. 5]:



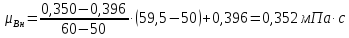

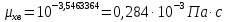


– коэффициент
диффузии бинарной смеси при
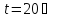
 ,
рассчитывают по приближенной формуле:
,
рассчитывают по приближенной формуле:
 ,
(1.3.7)
,
(1.3.7)
где
 –
динамический коэффициент вязкости
жидкости при
–
динамический коэффициент вязкости
жидкости при
 ;
;
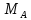 и
и
 – мольные массы исходных веществ,
– мольные массы исходных веществ, [5, с. 3];
[5, с. 3];
 –мольные
объёмы растворённого вещества и
растворителя,
–мольные
объёмы растворённого вещества и
растворителя,
 ;
;
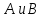 –коэффициенты,
зависящие от свойств растворённого
вещества и растворителя.
–коэффициенты,
зависящие от свойств растворённого
вещества и растворителя.
Динамический
коэффициент вязкости жидкости при

 рассчитываем по уравнению(1.3.6):
рассчитываем по уравнению(1.3.6):
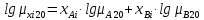 ,
,
где
 – динамические коэффициенты вязкости
легколетучего и труднолетучего
компонентов при
– динамические коэффициенты вязкости
легколетучего и труднолетучего
компонентов при ,
которые выбираем из таблицы зависимости
динамического коэффициента вязкости
органических жидкостей от температуры
[5, с. 5]:
,
которые выбираем из таблицы зависимости
динамического коэффициента вязкости
органических жидкостей от температуры
[5, с. 5]:





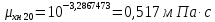
Мольные
объёмы
 находим по правилу аддитивности,
используя значения атомных объёмов [3,
с. 8]:
находим по правилу аддитивности,
используя значения атомных объёмов [3,
с. 8]:

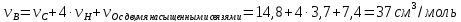
Значения
коэффициентов
 для смеси ацетон – метиловый спирт
находим из таблицы значений коэффициентов
для смеси ацетон – метиловый спирт
находим из таблицы значений коэффициентов для расчётов коэффициента диффузии в
бинарных смесях [3, с.9]:
для расчётов коэффициента диффузии в
бинарных смесях [3, с.9]:



– температурный
коэффициент
 для уравнения коэффициента диффузии
(см. ниже,(1.3.9))
определяют по эмпирической формуле:
для уравнения коэффициента диффузии
(см. ниже,(1.3.9))
определяют по эмпирической формуле:
 ,
(1.3.8)
,
(1.3.8)
где
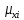 – динамический коэффициент вязкости
жидкости при
– динамический коэффициент вязкости
жидкости при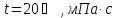 (см. выше);
(см. выше);
 –плотность
жидкости при
–плотность
жидкости при
 ,
которую определяют по уравнению(1.3.5):
,
которую определяют по уравнению(1.3.5):
 ,
,
где
 – плотности легколетучего и труднолетучего
компонентов при
– плотности легколетучего и труднолетучего
компонентов при ,
которые выбираем из таблицы плотностей
жидкостей в зависимости от температуры
[5, с. 4]:
,
которые выбираем из таблицы плотностей
жидкостей в зависимости от температуры
[5, с. 4]:








– коэффициенты
диффузии
 рассчитывают по приближенной формуле:
рассчитывают по приближенной формуле:
 (1.3.9)
(1.3.9)


– поверхностные
натяжения
 определяют по уравнению:
определяют по уравнению:
 ,
(1.3.10)
,
(1.3.10)
где
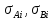 – поверхностные натяжения исходных
веществ при соответствующих температурах,
– поверхностные натяжения исходных
веществ при соответствующих температурах, ,
определяемые интерполированием данных
таблицы поверхностных натяжений
органических веществ и воды в зависимости
от температуры [3, с. 10]:
,
определяемые интерполированием данных
таблицы поверхностных натяжений
органических веществ и воды в зависимости
от температуры [3, с. 10]:
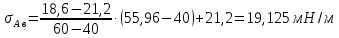







– удельные теплоёмкости питания, кубового остатка и дистиллята уже были определены по аддитивной формуле (1.2.2)
– массовые
расходы
 рассчитывают по уравнениям:
рассчитывают по уравнениям:
 ,
(1.3.11)
,
(1.3.11)
где
молярная масса дистиллята
 определяется по формуле(1.3.3):
определяется по формуле(1.3.3):
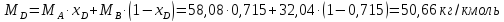

 ,
(1.3.12)
,
(1.3.12)
где
молярная масса исходной смеси
 определяется по формуле(1.3.3):
определяется по формуле(1.3.3):


– объёмные
расходы
 рассчитывают по соотношению:
рассчитывают по соотношению:
 (1.3.13)
(1.3.13)


б) Для паровой фазы в верхней и нижней частях колонны:
– мольные
составы
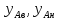 определяют по уравнениям рабочих линий
при подстановке в них соответственно
определяют по уравнениям рабочих линий
при подстановке в них соответственно
 :
:


– мольные
массы
 определяют
по уравнению (1.3.3)
при соответствующих значениях
определяют
по уравнению (1.3.3)
при соответствующих значениях
 :
:


– массовые
составы
 определяют по уравнению:
определяют по уравнению:
 (1.3.14)
(1.3.14)

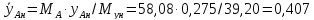
– средние
температуры
 определяют, используя данные таблицы
равновесия пар – жидкость бинарной
системы ацетон – метиловый спирт [2, с.
5] при соответствующих значениях
определяют, используя данные таблицы
равновесия пар – жидкость бинарной
системы ацетон – метиловый спирт [2, с.
5] при соответствующих значениях и
и :
:


– плотности
паров веществ

 ,
при средних температурах определяют
по уравнению Клапейрона (при
,
при средних температурах определяют
по уравнению Клапейрона (при
 ):
):
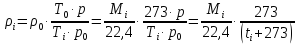 ,
(1.3.15)
,
(1.3.15)
где
 – плотность пара при нормальных условиях,
– плотность пара при нормальных условиях,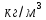 ;
;
 –средняя
температура пара,
–средняя
температура пара,
 ;
;
 –среднее
давление в колонне,
–среднее
давление в колонне,





плотности
 рассчитывают по уравнению:
рассчитывают по уравнению:
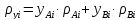 (1.3.16)
(1.3.16)
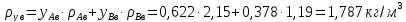

– динамические
коэффициенты вязкости
 рассчитывают по приближенной формуле:
рассчитывают по приближенной формуле:
 (1.3.17)
(1.3.17)
где
 – динамические коэффициенты вязкости
паров легколетучего и труднолетучего
компонентов при соответствующих
температурах,
– динамические коэффициенты вязкости
паров легколетучего и труднолетучего
компонентов при соответствующих
температурах, ,
которые находим, интерполируя данные
таблицы зависимости динамического
коэффициента вязкости пара от температуры
[5, с. 8]:
,
которые находим, интерполируя данные
таблицы зависимости динамического
коэффициента вязкости пара от температуры
[5, с. 8]:






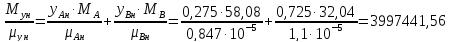

– коэффициенты
диффузии
 рассчитывают по приближенной формуле:
рассчитывают по приближенной формуле:
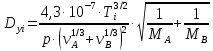 ,
(1.3.18)
,
(1.3.18)
где
 – средняя температура пара,
– средняя температура пара,
 ;
;
 –среднее
давление в колонне,
–среднее
давление в колонне,
 ;
остальные обозначения см. для уравнения(1.3.7).
;
остальные обозначения см. для уравнения(1.3.7).


– удельная теплота конденсации паров дистиллята была рассчитана выше (см. уравнение (1.2.4))
– массовые
расходы
 определяют по уравнению:
определяют по уравнению:
 (1.3.19)
(1.3.19)


– объёмные
расходы пара
 рассчитывают по соотношению:
рассчитывают по соотношению:
 (1.3.20)
(1.3.20)


