kr_6_10

Задание №1

Измените порядок интегрирования

Решение:

Данная область интегрирования определена такими неравенствами: 

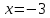
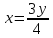
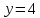
Найдем точку пересечения графика функции :

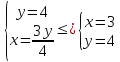
Найдем точку пересечения графика функци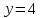и и :

Для изменения порядка интегрирования разобьем область интегрирования на три: D₁ , D₂ и D₃. 

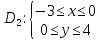
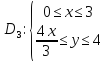
Задание №2

Вычислите двойной интеграл

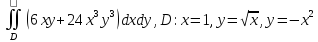
Решение:

Изобразим область интегрирования.

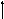
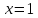
Из чертежа видим, что , а у изменяется от до .

Тогда:

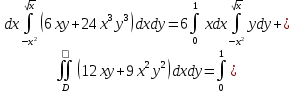
Задание №3

Вычислить площадь фигуры, ограниченной заданными линиями.

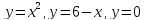
Решение:

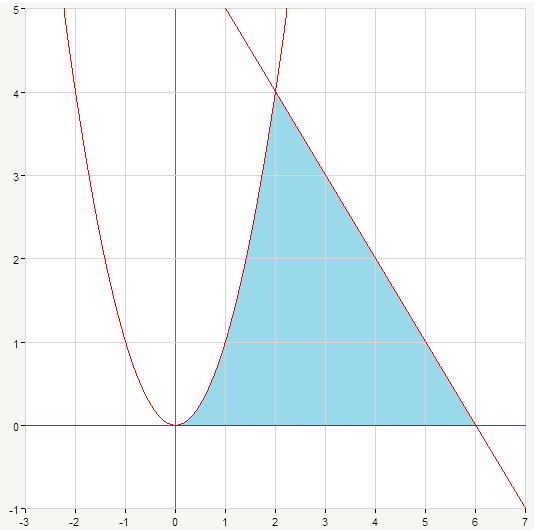
Начертим графики данных функций:

Из графика видно, что точка пересечения графика функции

(2; 4).

Также эти точки можно найти, решив систему уравнений:

Площадь искомой фигуры можно представить следующим образом:

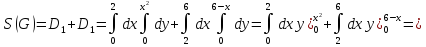
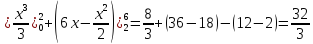
Задание №4

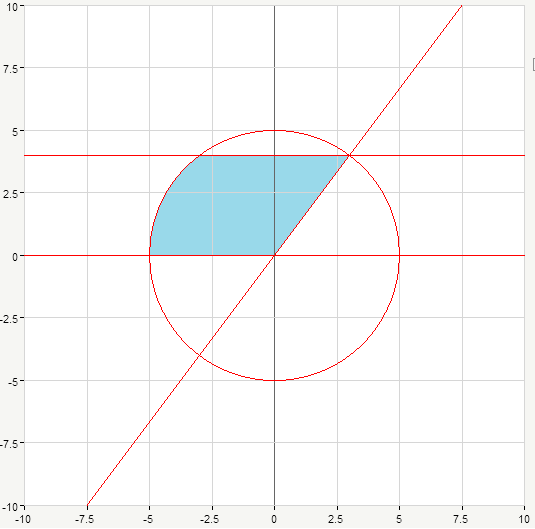
Вычислите объем тела, ограниченного данными поверхностями.

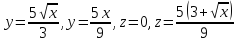
Решение:

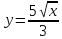– полупараболический цилиндр, – плоскость, параллельная оси Oy

z = 0 – плоскость xOy, .

Рис. 1. Проекция области G на плоскость xOy

Найдем точку пересечения графика функции :
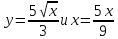