kr_7_10

Задание №1

Вычислите криволинейный интеграл первого рода по данной линии.

Решение:

Составим уравнения прямой, проходящей через точки A и B:

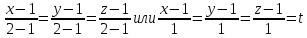
Таким образом, получаем параметрические уравнения прямой:

По формуле находим:

Задание №2

Вычислите работу силы при перемещении вдоль линии L от точки А до точки В.

Решение:

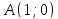
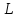
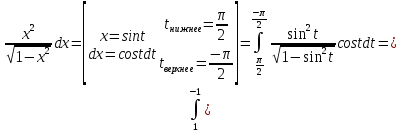
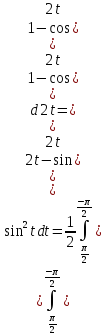
Задание №3

Вычислите поверхностный интеграл первого рода по поверхности S, где S часть плоскости , отсеченная координатными плоскостями.

Решение:

Запишем уравнение плоскости в виде

Найдем частные производные

Применяя формулу

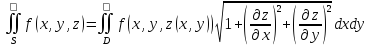
поверхностный интеграл можно выразить через двойной интеграл:

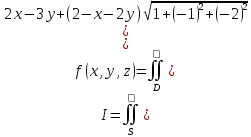
Область интегрирования D представляет собой треугольник, показанный ниже на рисунке:

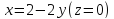
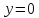
D

Вычисляем окончательно заданный интеграл:

Задание №4

Вычислите поверхностный интеграл второго рода по поверхности S, где S часть плоскости 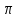, отсеченная координатными плоскостями, в направлении нормали, образующей острый угол с осью Oz.

Решение: