3.2.2 Решение задачи в общем виде. Симплексная таблица

Вернемся к решению задачи в общем виде из раздела 3.2, начиная с исходного опорного плана Х = (b₁, b₂, . . . b_m,). Обозначим z целевую функцию задачи. На исходном плане значение целевой функции, так как слагаемые, соответствующие небазисным переменным, обратятся в 0.

Для применения симплекс-метода к системе необходимо приписать еще одно ограничение - критериальное: z -= 0.

В решенном примере это было четвертое ограничение. Поскольку в этом примере базисные переменные исходного опорного плана (х_5-7) не входили в целевую функцию, то и в критериальное ограничение они не вошли. В общем случае это не так. Например, если бы задача имела вид:

max-5х₁+ 2х₃

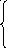-2,5х₁– 0,5х₂+ х₃+ 0,5х₅ = 1

1,5х₁+ 0,5х₂+ х₄ - 0,5х₅ + х₆= 4

-3х₁+ 5х₄ + х₇= 7

х_1-70

то в качестве базисных в исходном опорном плане следовало бы взять переменные х₃, х₆и х₇. Одна из них - х₃- входит в целевую функцию. Уравнение z -= 0 здесь приняло бы вид:z+ 5х₁- 2х₃= 0. Чтобы увеличитьz, здесь следовало бы увеличить х₃. Но переменная х₃и так является базисной, уже равна 1, и из ограничений следует, что увеличить ее до большего значения невозможно. Такое затруднение возникло из-за того, что после добавления критериального ограничения столбцы коэффициентов перестали быть единичными. Базисные переменные должны входить в него с нулевыми коэффициентами, а в последней задаче это не так.

Чтобы избежать этого, выразим базисную переменную х₃ из первого ограничения через небазисные (-2,5х₁– 0,5х₂+ х₃+ 0,5х₅= 1х₃= 1 + + 2,5х₁+ 0,5х₂- 0,5х₅) и подставим в целевую функцию: z = -5х₁+ 2х₃= -5х₁+ + 2*(1 + 2,5х₁+ 0,5х₂- 0,5х₅) = 2 + х₂- х₅. Теперь уравнение z -= 0 примет вид:z+ х₂- х₅= 2, т.е. вид уравнения (4`) из системы (16). Рекомендуется сравнить остальные ограничения последней задачи с уравнениями (16): они в точности совпадают; и целевая функция взята из того же примера.

Итак, в общем случае после введения критериального ограничения столбцы при базисных переменных могут перестать быть единичными. Чтобы избежать этого, выразим базисные переменные x_1-mиз ограничений через небазисные:

x₁ = b₁ - a_{1 m+1}x_m+1 - . . . -a_{1 n}x_n

…

x _i = b _i - a _{i m+ 1}x_{m+ 1} - . . . -a _{i n}x_n

…

x_m = b_m - a_{m m+1}x_m+1 - . . . -a_{m n}x_n

и подставим их в целевую функцию: z==c₁(b₁- -a_{1 m+1}x_m+1- . . . -a_{1 n}x_n) + . . . +c_m(b_m-a_{m m+1}x_m+1- . . . -a_{m n}x_n) +c_m+1x _m+1+ . . . + + c_nx_n.

После приведения подобных членов и переноса свободного члена в правую часть критериальное ограничение примет следующий вид: z+x_m+1(c₁a_{1 m+1}+ . . .+ c_ma_{m m+1} - c _m+1) + . . . + x_n(c₁a_{1 n}+ . . . + c_ma_{m n} - c_n) = c₁b₁ + + . . . +c_mb_m; илиx_m+1(-c_m+1) + … +x_n(-c_n) =.

Обозначим коэффициенты при переменных x_jв критериальном ограничении -_j = -c_j; а свободный член этого ограничения -d=.

Отметим, что коэффициенты при базисных переменных в критериальном ограничении будут нулевыми, что и требовалось получить. Но и эти нулевые коэффициенты также можно рассчитать по формулам (-c_j): поскольку базисные переменные входят лишь в одно ограничение, в этих формулах только одно слагаемое в сумме слева будет ненулевым. Для базисных переменных.

Таким образом, критериальное ограничение примет вид:

z+= d

Теперь исходные данные задачи линейного программирования можно записать в виде симплексной таблицы(таблица 7).

Каждая строка таблицы соответствует одному ограничению задачи линейного программирования ((m+1)-я строка - критериальному ограничению).

Левая часть таблицы (первые три столбца) является вспомогательной - в ней в первом столбце указывается номер строки, во втором (x_б) - базисная переменная, соответствующая каждой строке (та, которая входит в это ограничение с коэффициентом 1), в третьем (с_б) - коэффициент целевой функции при соответствующей базисной переменной.

В правой части таблицы в столбце В указаны свободные члены системы ограничений (в (m+1)-ой строке - значение целевой функции на опорном плане d), а все остальные столбцы соответствуют переменным задачи линейного программирования, и в них указаны коэффициенты при этих переменных в каждом ограничении.

Над обозначениями переменных в верхней части таблицы рекомендуется указывать соответствующие коэффициенты целевой функции.

Таблица 7 – Симплексная таблица

				c1	. . .	cj	. . .	cn
№	xб	cб	В	х1	. . .	хj	. . .	хn
1	. . .	. . .	b1	a 11	. . .	a 1j	. . .	a1n
. . .	. . .	. . .	. . .	. . .	. . .	. . .	. . .	. . .
i	. . .	. . .	bi	a i1	. . .	aij		ain
. . .	. . .	. . .	. . .	. . .	. . .	. . .	. . .	. . .
m	. . .	. . .	bm	a m1	. . .	a mj	. . .	amn
m+1			d	1	. . .	j	. . .	n

Идея дальнейшего решения заключается в том, чтобы в критериальном ограничении увеличивать первое слагаемое (z) за счет уменьшения суммы остальных (свободный член - постоянная величина). При этом в той сумме, которую необходимо уменьшить, отличные от нуля коэффициенты стоят только при небазисных переменных (так как базисным соответствуют единичные столбцы). Небазисные переменные равны нулю, их значения можно только увеличивать. При этом увеличиваться должны значения тех небазисных переменных, при которых стоят отрицательные коэффициенты _j(чтобы сумма уменьшалась)_. Однако увеличение этих переменных ограничивается другими уравнениями системы.

Лемма 1 (критерий оптимальностиплана). Если все_j0, то текущий опорный план - оптимальный.

Доказательство следует из того, что небазисные переменные равны нулю. Их можно только увеличивать, при этом, так как_j0, то целевая функция уменьшается, так как в уравненим (z+= d) значениеd- const.

Рассмотрим исходную симплексную таблицу для решенного выше примера (таблица 8). Поскольку для расчетов предполагается использовать средства электронной таблицы MicrosoftExcel, слева и сверху от таблицы 8 указаны номера строк и столбцов электронной таблицы.

В диапазон ячеек D1:К5 введены исходные данные примера. Исходя из них, заполнена вспомогательная часть таблицы в А2:С5. ВD6 введена формула =-D1, которая затем скопирована по строке до К6 (таким образом введены свободный член и коэффициенты критериального ограничения).

Таблица 8 – Исходная симплексная таблица

	A	B	C	D	E	F	G	H	I	J	K
1					-5	0	2	0	0	0	0
2	N	xб	cб	B	x1	x2	x3	x4	x5	x6	x7
3	1	x5	0	2	-5	-1	2	0	1	0	0
4	2	x6	0	5	-1	0	1	1	0	1	0
5	3	x7	0	7	-3	0	0	5	0	0	1
6	m+1			0	5	0	-2	0	0	0	0

Таким образом, в таблице 8 записана система (15).

Итак, если все _j0, то задача решена (это критерий оптимальности для задачи на максимум). Если это не так, необходимо перейти к другому опорному плану. Для этого выберем столбец таблицы, в котором нарушен критерий оптимальности, т.е. некоторыйk-й столбец, такой, что_k< 0. Этот столбец называют разрешающим (очевидно, он не базисный, так как иначе было бы_k= 0). Преобразуем симплексную таблицу таким образом, чтобы переменная х_квошла в базис (т.е. в набор базисных переменных), а некоторая другая переменная из него вышла.

В этом примере среди коэффициентов _jесть отрицательный:₃= -2 < 0 (k= 3). Поэтому при преобразовании системы (15) в систему (16) в базис входила переменная x₃. Далее в разделе 3.2.1 мы определяли, какую переменную следует вывести из базиса, и для этого подсчитывали отношения 2/2 и 5/1.

Для выбора переменной, которая должна выйти из базиса, для всех положительных элементов k-го столбца подсчитывают отношения b_i/a_iки выбирают из них наименьшее. Соответствующую строку (пусть это будет t-ая строка) также называют разрешающей, а коэффициент а_tk- разрешающим элементом.

В таблице 8 положительные a_iк= a_i3находятся в первой и второй строках. Наименьшее из отношений b_i/a_iксоответствует первой строке:min{b₁/a₁₃; b₂/a₂₃} = {2/2; 5/1} = {1; 5} = 1. Таким образом, разрешающая строка - первая, т.е. t = 1. Разрешающий элемент а_tk= а₁₃= 2. В таблице 8 он выделен заливкой. При преобразовании системы (15) в систему (16) из базиса выходила переменная x₅, которая соответствует первой строке.

Левая (вспомогательная) часть новой таблицы будет отличаться только содержанием t-й строки столбцов х_би с_б: вместо х_tи с_t там будет стоять соответственно х_ки с_к, так как переменная х_tиз базиса выйдет, а х_квойдет.

Правая часть таблицы подвергнется преобразованию методом Гаусса. Цель преобразования - получить единичный столбец при переменной х_к, причем единица должна будет стоять на месте разрешающего элемента, т.е. в t-ой строке. Общие формулы для таких преобразований выглядят следующим образом (со штрихом обозначены элементы новой таблицы):

а_tj`= а_tj/ а_tk;

b_t`= b_t / а_tk– вся разрешающая строка делится на разрешающий элемент, при этом на его месте получают 1;

а_ij`= а<sub>ij</sub> - а<sub>tj</sub>`* а_ik= а_ij - а_tj * а_ik/ а_tk;

b_i`= b<sub>i</sub> - b<sub>t</sub>`* а_ik= b_i - b_t * а_ik/ а_tk– из всех остальных строк вычитают преобразованную разрешающую строку, умноженную на элемент, стоящий в преобразуемой строке в разрешающем столбце (при этом на его месте получают 0, так как из него вычитают его же, умножив на 1);

_j`=<sub>j</sub> - а<sub>tj</sub>`*_k=_j- а_tj *_k/ а_tk ;

d`= d - b<sub>t</sub>`*_k= d - b_t *_k/ а_tk– то же самое делают с критериальной строкой.

Докажем, что при применении этих формул мы действительно сможем построить новый план по тому же правилу (приравняв базисные переменные к свободным членам). Для этого нужно, чтобы новые свободные члены оказались неотрицательными, иначе такой план не будет допустимым.

Лемма 2 (окритерии допустимоститаблицы).При преобразовании таблицы она сохраняет допустимость, т.е. b_i`0,i.

Доказательство.

Свободные члены вычисляются по формуле b_i`= b_i - b_t * а_ik/ а_tk.

Здесь b_i, b_t0 (т.к. предыдущая таблица – допустимая); а_tk> 0 (по способу выбора разрешающего элемента).

Если а_ik 0 , то b_i`0 (к неотрицательному числу прибавляют неотрицательное).

Если а_ik> 0, то разделим обе части неравенства b_i - b_t * а_ik/ а_tk0 на а_ik. Получим: b_i - b_t * а_ik/ а_tk0b_i / а_ik- b_t/ а_tk  0 b_i / а_ikb_t/ а_tk

Последнее неравенство истинно по способу выбора разрешающего элемента. Следовательно, будет истинно и первое из этих трех неравенств, т.е. b_i`0.

Лемма доказана.

Таким образом, при правильном выборе разрешающего элемента преобразованной системе уравнений по-прежнему можно поставить в соответствие опорный план так же, как это делалось для исходной таблицы.

Лемма 3 (об изменении значения целевой функции).При переходе к следующему опорному плану значение целевой функции не убывает: d`d.

Доказательство. Новое значение целевой функции вычисляется по формуле d`= d - b_t *_k/ а_tk. Здесь а_tk> 0,_k< 0, b_t0.

Если b_t > 0, то d`> d.

Есди b_t = 0, то d`= d.

Лемма доказана.

Лемма 4 (о неограниченности целевой функции). Если в разрешающем столбце нет возможности выбрать разрешающий элемент (нет положительных элементов, все а_ik0), то целевая функция задачи линейного программирования не ограничена.

Доказательство.Пусть_k< 0, все а_ik0.

Х^о= (b₁, . . .,b_m, 0, . . ., 0) - исходный опорный план;k-я переменная - небазисная.

Рассмотрим семейство планов:

Х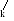^()= (b₁-a_1k,b₂-a_2k,. . .,b_m-a_mk, 0, . . ., 0,, 0, . . .,0),0.

Эти планы допустимые. В самом деле, так как все а_ik0, все переменные здесь неотрицательные. В выполнении остальных ограничений легко убедиться, подставив эти планы в систему ограничений задачи (14). В самом деле, в каждом ограничении при этом будет получено:

b_i–a_ik*+a_ik*=b_i

Последнее ограничение будет иметь вид: z + = d. Подставим в него план Х^(). При этом все слагаемые при небазисных переменных, кроме –го, обратятся в ноль (при небазисных тоже, потому что при этих переменных коэффициенты в критериальном ограничении равны нулю).

z + _k*= d; z = d -_k*. Так как_k<0,+z+(при стремлении к бесконечности значение целевой функции тоже будет стремиться к плюс бесконечности). Таким образом, на допустимых планах целевая функция может принимать неограниченно большие значения.

Лемма доказана.

Теорема о сходимости симплекс-метода. Если после каждого этапа симплекс-метода значение целевой функции возрастает, то алгоритм дает решение задачи линейного программирования в конечное число шагов.

Доказательство. На каждом этапе мы получаем текущий опорный план (вершину ОДП). Число опорных планов конечно (не больше, чем число способов выбора m переменных из n -^*). Так как по предположению целевая функция возрастает, то мы второй раз не получим пройденный план, а значит, в конечное число этапов получим решение.

Целевая функция не убывает по лемме 3. Если ее значение не изменяется, то возможно зацикливание (хотя оно встречается довольно редко). В систему может быть вставлен специальный блок для проверки на зацикливание. По той же лемме 3 значение целевой функции может не измениться только если b_t = 0, т.е. в очередном опорном плане базис был вырожденным.

Из формулы для пересчета целевой функции (d`= d - b_t *_k/ а_tk) следует, что при выборе разрешающего столбца можно заранее определить, на сколько изменится ее значение: на_k* b_t / а_tk. Следовательно,если критерий оптимальности нарушен не в одном, а в нескольких столбцах таблицы, то выбрать в качестве разрешающего лучше тот из них, для которого это изменение будет больше. Тогда решение задачи может быть получено быстрее, за меньшее число этапов.

Вторая симплексная таблица для решенного примера примет вид таблицы 9.

Для того, чтобы получить ее в MicrosoftExcel, следует скопировать диапазон ячеек А1:К6 на диапазон А7:К11. Затем отредактируем вспомогательную часть таблицы: в В8 вместо x₅введем x₃, а в С8 вместо 0 введем 2.

Затем отредактируем диапазон D8:К11. Для этого в D8 введем формулу =D3/$G3^*. Она вводится для того, чтобы обе части третьего ограничения разделить на G3, т.е. на 2.

В D9 введем формулу =D4-D$8*$G4. Скопируем последнюю формулу на диапазон ячеек D10:D11. В результате в D10 появится формула =D5-D$8*$G5, а в D11 формула =D6-D$8*$G6. Это делается для того, чтобы из всех остальных строк, кроме разрешающей, вычесть преобразованную разрешающую (она в 8-й строке электронной таблицы), умноженную соответственно на 1 (в G4), 0 (в G5) и -2 (в G6).

Выделим формулы в диапазоне D8:D11 и скопируем их на диапазон ячеек Е8:К11. В результате столбец коэффициентов при x₃станет единичным.

Таблица 9 – Вторая симплексная таблица

	A	B	C	D	E	F	G	H	I	J	K
7	N	xб	cб	B	x1	x2	x3	x4	x5	x6	x7
8	1	х3	2	1	-2,5	-0,5	1	0	0,5	0	0
9	2	x6	0	4	1,5	0,5	0	1	-0,5	1	0
10	3	x7	0	7	-3	0	0	5	0	0	1
11	m+1			2	0	-1	0	0	1	0	0

Таким образом, в таблице 9 записана система (16).

Отметим, что для пересчета критериального ограничения можно использовать два способа:

а) описанный выше метод Гаусса (поскольку это такое же линейное ограничение, как и остальные mограничений);

б) можно заново перестроить его по выведенным ранее формулам _j = - c_j; d =(по своей сути это означает выражение базисных переменных из ограничений через небазисные и подстановку их в критериальное ограничение).

При использовании для расчетов электронной таблицы способ (а) предпочтительнее.

Тем не менее, если ввести в D11 другую формулу =СУММПРОИЗВ($C8:$C10;D8:D10)-D1, и именно ее скопировать по строке до К11, то результат вычислений получится тем же самым, что приведен в таблице 9. В самом деле, d= 2*1 + 0*4 + 0*7 – 0 = 2 (здесь, в отличие от других столбцов, вычитать 0 не обязательно, но ячейка D1 все равно нулевая);₁= 2*(-2,5) + 0*1,5 + 0*(-3) – (-5) = 0;₂ = 2*(-0,5) + 0*0,5 + 0*0 – - 0 = -1; коэффициент при базисной переменной₃== 2*1 + 0*0 + 0*0 – 2 = 0 и т.д.

Если в исходной симплексной таблице базисные переменные входят в целевую функцию, то в ней построить критериальную строку можно только способом (б).

В таблице 9 критерий оптимальности нарушен в столбце коэффициентов при x₂. Положительный коэффициент в этом столбце только один – 0,5. Это разрешающий элемент, в таблице 9 он выделен. Следовательно, x₂войдет в базис вместо x₆. В результате преобразований будет получена таблица 10.

Для того, чтобы получить эту таблицу, диапазон ячеек А7:К11 скопируем на диапазон А12:К16. В В14 вместо x₆введем x₂. Затем отредактируем диапазонD13:К16. Для этого в D14 введем формулу =E9/$F9. Она вводится для того, чтобы обе части второго (разрешающего) ограничения разделить на F9, т.е. на 0,5. В D13 введем формулу =D8-D$14*$F8. Скопируем последнюю формулу на диапазон ячеек D15:D16. Это делается для того, чтобы из всех остальных строк, вычесть преобразованную разрешающую, умноженную соответственно на -0,5, 0 и -1.

Выделим формулы в диапазоне D13:D16 и скопируем их на диапазон ячеек Е13:К16. В результате столбец коэффициентов при x₂станет единичным.

Тот же результат был бы получен, если бы в D16 вместо формулы =D11-D$14*$F11 стояла формула =СУММПРОИЗВ($C13:$C15;D13:D15)-D1, и именно она была бы скопирована на диапазон Е16:К16.

Таблица 10 – Оптимальная симплексная таблица

	A	B	C	D	E	F	G	H	I	J	K
12	N	xб	cб	B	x1	x2	x3	x4	x5	x6	x7
13	1	х3	2	5	-1	0	1	1	0	1	0
14	2	x2	0	8	3	1	0	2	-1	2	0
15	3	x7	0	7	-3	0	0	5	0	0	1
16	m+1			10	3	0	0	2	0	2	0

Таким образом, в таблице 10 записана система (17).

В критериальном ограничении последней симплексной таблицы нет отрицательных коэффициентов. Следовательно, оптимальный план найден. А именно, небазисные переменные x₁= x₄= x₅= x₆= 0, а базисные (их список находится в столбцеx_б) равны свободным членам (в столбце В): x₃= 5, x₂= 8, x₇= 7. Оптимум равен 10.

Итак, Х^(*)= Х⁽²⁾= (0; 8; 5; 0; 0; 0; 7),z^(*)=z⁽²⁾= 10.

Алгоритм симплекс-метода можно представить в виде блок-схемы, приведенной на рисунке 26.

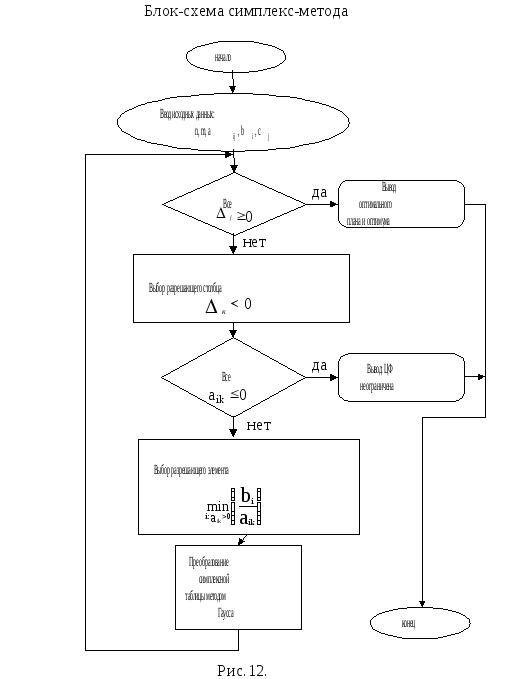
Рисунок 26 – Блок-схема симплекс-метода

Решение задачи на минимум отличается только критерием оптимальности - все коэффициенты критериального ограничения должны быть неположительны (соответственно, разрешающий столбец выбирается по положительному элементу).

При решении задач целесообразно соблюдать следующие рекомендации:

а) Если среди ограничений задачи линейного программирования имеются неравенства, или не все переменные являются неотрицательными, начните решение с приведения задачи к канонической форме. Проверьте, все ли свободные члены неотрицательны, и имеется ли базис. Если нет, проверьте, нельзя ли этого добиться простыми преобразованиями.

б) Чтобы избежать ошибки, разрешающий элемент в таблице следует выделять.

в) На каждой итерации симплекс-метода целесообразно проверять, соблюдены ли в таблице следующие элементарные правила:

1) Не должен нарушаться критерий допустимости. Отрицательный элемент в столбце В - признак ошибки в расчетах, причем скорее всего она была допущена при выборе разрешающей строки.

2) Должен присутствовать полный набор единичных столбцов при базисных переменных, причем единица должна стоять в той строке, которой эта переменная соответствует, а в остальных - нули.

3) Одно из средств контроля правильности вычислений - подсчет критериальной строки двумя способами: методом Гаусса и через сумму произведений (результаты должны совпадать).

4) При переходе к следующей симплексной таблице значение целевой функции должно, по крайней мере, не убывать (если задача на максимум) или не возрастать (если она на минимум).

Несоблюдение этих правил лишает смысла все остальные действия.

г) Из заключительной симплексной таблицы необходимо извлечь решение задачи линейного программирования или указать, почему она неразрешима.