5.6 Пример решения сопряженных задач

5.6.1 Задача, двойственная задаче о диете

Проиллюстрируем выполнение теорем двойственности на примере задачи о диете (см. раздел 1.3.1).

Построим задачу, двойственную к задаче о составлении рациона, решение которой было найдено в разделе 4.2 (в которой минимальное содержание белка в рационе должно составлять 44 г, а не 110 г).

Для этого вначале необходимо добиться, чтобы во всех неравенствах прямой задачи стоял знак (так как задача на минимум), т.е. умножить обе части второго и четвертого ограничения на -1:

min 4х₁+ 15х₂ + 40х₃

3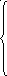80х₁ + х₂+ 2х₃4

-380х₁ - х₂- 2х₃-6

90х₂+ 50х₃44

-20х₂- 80х₃-25

х₁+ х₂ + х₃ = 0,5

х_1-3 0

Построим задачу, двойственную к данной^*:

max4y₁– 6y₂+ 44y₃– 25y₄+ 0,5у₅

3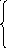80y₁– 380y₂+ у₅4

y₁–y₂+ 90y₃– 20y₄+ у₅ 15

2y₁– 2y₂+ 50y₃– 80y₄+ у₅ 40

у_1-4 0

Чтобы решить ее симплекс-методом, приведем ее к канонической форме. Для этого нужно ввести три дополнительных переменных. Кроме того, поскольку переменная у₅не ограничена по знаку (т.к. она соответствует уравнению прямой задачи), следует заменить ее на разность двух неотрицательных переменных (у₅= у₅`- у₅``):

max4y₁– 6y₂+ 44y₃– 25y₄+ 0,5у₅` – 0,5у₅``

380y₁– 380y₂+ у₅` – у₅``+y₆= 4

y₁–y₂+ 90y₃– 20y₄+ у₅` – у₅``+y₇= 15

2y₁– 2y₂+ 50y₃– 80y₄+ у₅` – у₅``+y₈= 40

у_{1-4, 6-8,} у₅`, у₅``0

В этой задаче имеется готовый базис, и можно сразу же решить ее симплекс-методом, не используя метод искусственного базиса^*. Решение приведено в таблице 20.

Таблица 20 – Решение двойственной задачи

				4	-6	44	-25	0,5	-0,5	0	0	0
N	xб	cб	B	у1	у2	у3	у4	у5`	у5``	у6	у7	у8
1	у6	0	4	380	-380	0	0	1	-1	1	0	0
2	у7	0	15	1	-1	90	-20	1	-1	0	1	0
3	у8	0	40	2	-2	50	-80	1	-1	0	0	1
m+1			0	-4	6	-44	25	-0,5	0,5	0	0	0
N	xб	cб	B	у1	у2	у3	у4	у5`	у5``	у6	у7	у8
1	у6	0	4	380	-380	0	0	1	-1	1	0	0
2	у3	44	0,167	0,011	-0,011	1	-0,222	0,011	-0,011	0	0,011	0
3	у8	0	31,67	1,444	-1,444	0	-68,89	0,444	-0,444	0	-0,556	1
m+1			7,333	-3,511	5,511	0	15,222	-0,011	0,011	0	0,489	0
N	xб	cб	B	у1	у2	у3	у4	у5`	у5``	у6	у7	у8
1	у5`	0	4	380	-380	0	0	1	-1	1	0	0
2	у3	44	0,122	-4,211	4,211	1	-0,222	0	0	-0,011	0,011	0
3	у8	0	29,889	-167,44	167,44	0	-68,89	0	0	-0,444	-0,556	1
m+1			7,378	0,711	1,289	0	15,222	0	0	0,011	0,489	0