1.4.4 Примеры приведения задачи линейного программирования к канонической и стандартной формам и ее записи в матричной форме

Рассмотрим задачу на max, содержащую три ограничения на три переменных:

max х₁+ 2х₂+ х₃

3х₁+ х₂- х₃8

х₁- 2х₂+ 4х₃= 5

2х₁+ 2х₂+ х₃10

х_1,2 0

Приведем эту задачу к канонической форме. Отметим, что на знак переменной х₃ никаких ограничений не накладывается. Поэтому заменим неограниченную по знаку переменную на разность двух неотрицательных (х₃ = х₃` - х<sub>3</sub>``; х<sub>3</sub>`, х₃``0). Кроме того, в задаче присутствуют два неравенства, поэтому введем две дополнительные переменные х₄ и х₅. С их помощью преобразуем первое и последнее ограничения по формулам соответственно (4) и (5). Задача в канонической форме примет вид:

max х₁+ 2х₂+ х₃` - х₃``

3х₁+ х₂- х₃` + х₃``+ х₄ = 8

х₁- 2х₂+ 4х₃` - 4х₃``= 5

2х₁+ 2х₂+ х₃` - х₃``- х₅ = 10

х_1,2, х₃`, х₃``0

Запишем эту задачу в канонической форме в матричной форме. Отметим, что в задаче теперь шесть переменных. Следовательно, вектора С и Х будут включать по шесть компонент, а в матрице А будет шесть столбцов. В первых двух столбцах будут стоять коэффициенты при переменных х₁и х₂, в третьем и четвертом – при х₃` и х₃``, а в двух последних – при дополнительных переменных. Итак, введем следующие обозначения:

С = (1; 2; 1; -1; 0; 0); B = ; A =; X =.

Матричная форма записи примет вид: .

Приведем эту же задачу:

max х₁+ 2х₂+ х₃

3х₁+ х₂- х₃8

х₁- 2х₂+ 4х₃= 5

2х₁+ 2х₂+ х₃10

х_1,2 0

- к стандартной форме на минимум.

При этом потребуется точно такая же замена переменной (х₃ = х₃` - х<sub>3</sub>``; х<sub>3</sub>`, х₃``0). Целевую функцию необходимо минимизировать, поэтому умножим выражение в целевой функции на (-1) по аналогии с формулой (9). Чтобы все ограничения системы имели вид неравенств со знаком, необходимо обе части первого ограничения умножить на (-1) по аналогии с формулой (7). Второе ограничение (уравнение) заменим на два неравенства по аналогии с формулой (8). Задача в стандартной форме примет вид:

min -х₁- 2х₂- х₃` + х₃``

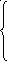-3х₁- х₂+ х₃` - х₃``-8

х₁- 2х₂+ 4х₃` - 4х₃``5

-х₁+ 2х₂- 4х₃` + 4х₃``-5

2х₁+ 2х₂+ х₃` - х₃``10

х_1-2, х₃`, х₃``0

Запишем эту задачу в стандартной форме в матричной форме:

С = (-1; -2; -1; 1); B = ; A =; X =.

Матричная форма записи примет вид:.

Модель производственного планирования, построенная в разделе 1.1, имеет стандартную форму.

Запишем ее в матричной форме:

С = (108; 112); B = ; A =; X =;.

В разделе 1.4.1 эта задача была приведена к канонической форме. Рассмотрим запись и такой задачи в матричной форме:

С = (108; 112; 0; 0; 0); B = ; A =; X =;.

1.5 Вопросы и упражнения

1. Как ставится задача линейного программирования в общем виде?

2. Что такое целевая функция, ограничения, план, допустимый план, ОДП, оптимальный план и оптимум задачи линейного програмирования?

3. Приведите пример экономической интерпретации задачи линейного программирования.

4. Что означает решить задачу линейного программирования?

5. Какие существуют формы записи задачи линейного программирования?

6. Как привести задачу линейного программирования к канонической форме?

7. Как привести задачу линейного программирования к стандартной форме?

8. Приведите задачу производственного планирования к канонической форме и объясните экономический смысл дополнительных переменных.

9. Постройте математическую модель следующей экономической ситуации:

Кожаные изделия проходят обработку на трех производственных участках. Информация о производстве приведена в таблице 1:

Таблица 1 – Исходные данные задачи

Тип изделия	Производственные участки (затраты времени на обработку единицы изделия, час)			Прибыль на единицу
	Дубильный	Раскройный	Завершающий	изделия, $
А	0,2	0,6	-	6
Б	0,3	0,5	0,8	7
Резервы времени по участкам, час	320	400	160

Составить план выпуска продукции, максимизирующий прибыль.

10. Приведите задачу из пункта 9 к канонической форме и запишите в матричной форме.

*Здесь и далее исходные данные примера носят чисто гипотетический характер и не соответствуют реальным технико-экономическим показателям деятельности какого-либо конкретного предприятии.

*За исключением задач, в которых переменные могут принимать только целые значения.

*Исходные данные примера носят чисто гипотетический характер и не соответствуют ни реальным ветеринарным нормам, ни технико-экономическим показателям деятельности какого-либо конкретного предприятии.

24