3.15. Электропроводность в магнитном поле.
Совокупность явлений, связанных с действием магнитного поля на электрические (гальванические) свойства твердотельных проводников, называется гальваномагнитными явлениями.
Гальваномагнитные явления принято подразделять на поперечные и продольные в зависимости от относительного направления электрического тока, пропускаемого через образец, и внешнего магнитного поля.
Наиболее ярко проявляют себя
поперечные гальваномагнитные явления,
т.е. такие, когда внешнее магнитное поле
перпендикулярно току
через образец. Прежде всего, к ним
относятся эффект Холла – возникновение
электрической разности потенциалов в
направлении, перпендикулярном векторам
и
,
и поперечный магниторезистивный
эффект – изменение электрического
сопротивления проводника
под действием внешнего магнитного поля
,
перпендикулярного направлению тока
.
Продольный магниторезистивный
эффект заключается в небольшом изменении
продольной компоненты электрического
сопротивления
во внешнем поле
,
приложенном в направлении электрического
тока
.
В тонких пленках и проволоках
гальваномагнитные эффекты зависят от
формы и размеров образца. Однако с ростом
магнитного поля
эта зависимость исчезает.
Основной причиной гальваномагнитных явлений является искривление траекторий носителей заряда в магнитном поле.
Остановимся более подробно на
явлении, получившем название эффект
Холла по фамилии ученого, открывшего
его (
,
1855 – 1938 гг.).
3.15.1.Классический эффект Холла (1879 г.).
Если металлическую пластинку, вдоль
которой (в направлении оси
)
течет постоянный ток
,
поместить в магнитное поле
,
перпендикулярное к пластинке, то на её
боковых гранях (параллельных плоскости,
в которой лежат векторы
и
)
возникает разность потенциалов
.
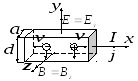В магнитном поле на заряженную
частицу действует
сила Лоренца, равная
.
(15.1)
Скорость (
частицы, магнитное поле (
)
и магнитную
составляющую
силы Лоренца можно записать через
их компоненты:
;
;
,
подчеркивая ортогональность векторных величин.
Действие силы Лоренца
в рассматриваемом случае эквивалентно
действию эффективного электростатического
поля
,
под действием которого носители тока
будут смещаться по оси
и накапливаться на нижней грани образца,
т.е. можно записать
В результате смещения зарядов в
сторону нижней грани и появления на
противоположной грани образца
нескомпенсированного электрического
заряда противоположного знака возникает
электрическое поле
,
противоположное по направлению полю
.
Процесс накопления заряда прекратится
(установится стационарное состояние),
когда поперечное электрическое поле
«уравновесит» действие силы Лоренца,
иными словами
,
или
.
Знак
в этом выражении означает, что для тока
положительных частиц поле
направлено против
оси
.
Вектор плотности тока
направлен вдоль оси
,
поэтому можем записать
,
и
,
где
- постоянная, или коэффициент Холла.
Холловская разность потенциалов (э.д.с. Холла) равна
.
Возникновение поперечной разности потенциалов было экспериментально обнаружено Е.Х. Холлом
в 1879 г., а само явление получило название эффекта Холла.
Перейдя от плотности тока
к силе тока
,
пропускаемого через образец, можем
записать
.
Все четыре величины, стоящие в правой
части выражения, измеряются в эксперименте,
что дает возможность определить из
опыта постоянную Холла и, следовательно,
концентрацию и знак носителей тока
(по знаку э.д.с. Холла). Измеряя одновременно
с постоянной Холла электропроводность
образца
,
можно найти также подвижность
носителей
,
т.е. получить важные сведения о проводящей
среде.
Все это позволяет понять значение измерения эффекта Холла как одного из основных методов исследования электрических свойств проводников и полупроводников.
Все сказанное выше справедливо для твердотельных сред, в которых проводимость осуществляется носителями одного типа (знака). Картина эффекта Холла значительно усложняется, когда в переносе электричества участвуют и электроны и дырки. Заряды разного знака будут дрейфовать в противоположные стороны, но смещаться в одном и том же направлении, т.е. накапливаться на одной и той же грани. При этом электроны и дырки могут иметь разные концентрации и характеризоваться различными значениями подвижности. В том случае, когда и подвижности и концентрации электронов и дырок одинаковы, их заряды будут полностью компенсировать друг друга и холловское поле будет равно нулю. В этом случае влияние магнитного поля проявится лишь в том, что на одной боковой грани образца концентрация носителей, а как следствие этого и локальная электропроводность повысятся, а на другой – понизятся. Впервые на существование этого эффекта указал А.Ф. Иоффе, а затем эффект наблюдался на опыте другими исследователями.
Рассматривая поведение электронов проводимости в магнитном поле, мы получили выражение
,
(*)
умолчав при этом, что в выражение для
силы Лоренца входит полная скорость
движения электрона, т.е., наряду со
скоростью дрейфа, еще и скорость его
беспорядочного теплового движения.
Учет скорости хаотического движения
не приводит к каким-либо серьезным
отклонениям от полученных нами результатов
(
),
хотя и дает несколько другое значение
постоянной Холла:
,
где
,
зависящая от механизма рассеяния
электронов и принимающая значения в
пределах от 1 до 2.