4.7 Векторный и скалярный потенциалы электромагнитного поля.

Записав систему уравнений Максвелла, теперь следует найти способ их решения. Для стационарных полей эта задача существенно облегчается введением вспомогательных величин – потенциалов и. Оказывается, что, видоизменив надлежащим образом определение скалярного и векторного потенциалов, можно воспользоваться ими и для решения уравнений Максвелла в общем случае, когда векторы электромагнитного поля зависят от времени.

Будем считать, что диэлектрическая и магнитнаяпроницаемости одинаковы на всем протяжении поля и поверхностных зарядов и токов в поле нет. При этих условиях векторыии их первые производные всюду остаются непрерывными, что существенно упрощает решение поставленной задачи.

Далее полученные результаты могут быть достаточно легко обобщены на случай наличия скачкообразного изменения ина отдельных поверхностях раздела различных сред, в то время как задача решения уравнений Максвелла при произвольной зависимостииот координат точки чрезвычайно усложняется.

В электростатике

, гдескалярный потенциал и,

т.е. поле вектора потенциально.

Изменяющееся во времени магнитное поле создает вихревое электрическое поле

,

т.е. полное электрическое поле приобретает непотенциальную составляющую.

Поскольку магнитных зарядов пока нет, то

и, как и раньше,,

где векторный потенциал.

Теперь, в общем случае, поля изависят от времени. Поэтому и потенциалыибудут зависеть от координат и от времени.

Выразим вихревое электрическое поле через векторный потенциал, воспользовавшись уравнениями

и:

, или,

откуда следует, что вектор -потенциальный, поэтому именно этот вектор может быть представлен в виде градиента скалярного потенциала:

. (7.1)

Итак, в общем случае вектор электрического поля выражается через векторный и скалярный потенциалы:

, (7.2)

где - поле электромагнитной индукции;- поле электрических зарядов.

Магнитное поле, по-прежнему описывается выражением

. (7.3)

Неоднозначность определения потенциалов. Калибровочное преобразование.

Как и в случае стационарных полей скалярный и векторныйпотенциалы определены неоднозначно, т.е. одно и то же электромагнитное поле может быть представлено различными значениями потенциалов.

Это связано с тем, что скалярный и векторный потенциалы поля являются лишь вспомогательными функциями, а непосредственный физический смысл имеют только напряженность электрического и индукциямагнитного полей. Именно эти характеристики поля однозначно определяют энергию поля, силы, действующие со стороны поля на заряженные частицы, плотность токов и т.д. Поэтому любые два поля, описываемые одними и теми же значениямии, но разными значениями потенциалови, физически тождественны.

Каков же произвол в определении потенциалов ипри заданных значениях векторови?

Пусть потенциалы электромагнитного поля связаны с силовыми характеристиками иуравнениями

,

.

Так как ротор градиента тождественно равен нулю, то если мы прибавим к вектору градиент произвольной скалярной функции

, (7.4)

то новому значению векторного потенциала будет соответствовать прежнее значение магнитной индукции

. (7.5)

Если не зависит от времени, то и значение напряженности электрического поляне изменится при заменена. Если же, т.е. является функцией времени, то значение векторасохранится неизменным, если одновременно с заменойбудет выполнена замена, причем

. (7.6)

Действительно,

. (7.7)

Т.о., напряженность и индукция электромагнитного поля остаются неизменными при одновременном прибавлении к векторному потенциалу градиента произвольной скалярной функции и вычитании из скалярного потенциала умноженной на коэффициент производной по времени от той же скалярной функции.

Преобразования

и(7.8)

носят название калибровочных преобразований.

Инвариантность поля по отношению к этому классу преобразований потенциалов называется калибровочной илиградиентнойинвариантностью.

Требование калибровочной инвариантности уравнений теоретической физики, т.е. требование, чтобы физическое содержание этих уравнений зависело только от напряженности и индукции электромагнитного поля и оставалось неизменным при всех преобразованиях потенциалов поля, играет важную роль в физических теориях. Решение отдельных конкретных задач часто облегчается специальной, целесообразной для данной задачи, калибровкой потенциалов.

Дифференциальные уравнения для потенциалов электромагнитного поля.

Пусть ,ина всем протяжении поля.

, (7.9)

. (7.10)

Подставим выражения ив уравнение (7.10):

; (7.11)

из векторной алгебры известно

. (7.12)

Тогда

, (7.13)

или

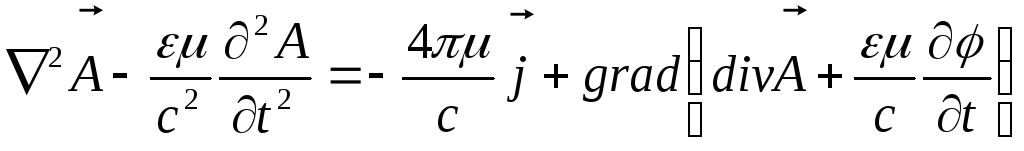. (7.14)

Воспользовавшись неоднозначностью определения потенциалов и, можем наложить некоторое условие, определяющее их взаимосвязь, в частности, так называемое, условие Лоренца:

. (7.15)

Тогда уравнение (7.14) для векторного потенциала в калибровке Лоренца приобретает вид:

. (7.16)

Вводя условие Лоренца, которое должно сохраняться при калибровочных преобразованиях, мы, т.о., накладываем ограничения на вид скалярной функции :

, (7.17)

т.е. условие Лоренца оказывается инвариантным лишь при калибровочных преобразованиях с функцией , удовлетворяющей уравнению:

. (7.18)

Воспользовавшись уравнением Максвелла

,

найдем теперь дифференциальное уравнение для скалярного потенциала , имея в виду уравнение (7.2)

,,

или

. (7.19)

Из условия Лоренца (7.15)

, (7.20)

поэтому

,

или

. (7.21)

Т.о., мы получили дифференциальные уравнения (7.16) и (7.21) для векторного и скалярного потенциалов, соответственно. Эти уравнения носят название уравнений Даламбера. Вместе сусловием Лоренцаони позволяют определить значения потенциалов электромагнитного поля по заданному распределению зарядов и токов проводимости.

Зная и, можно с помощью уравнений

и

найти векторы и.

Отметим, что хотя скалярный потенциал , как и в случае стационарных полей, зависит лишь от распределения зарядов, а векторный– от распределения токов проводимости, напряженность же электрического поля зависит не только от градиента скалярного потенциала, но и от производной по времени векторного потенциала. В этом обстоятельстве проявляется закон электромагнитной индукции.

Для стационарных полей все производные по времени обращаются в нуль, и все уравнения, как и следовало ожидать, сводятся к полученным ранее уравнениям, описывающим стационарные поля.

Пока остается открытым вопрос о физическом смысле коэффициента . Ответ на него мы получим чуть позже.