3.11. Диамагнетизм.

3.11.1. Ларморовская прецессия.

Как уже отмечалось, диамагнетизм присущ всем без исключения веществам, но наблюдается лишь у тех веществ, атомы которых в отсутствие внешнего поля не обладают магнитным моментом.

Чтобы представить, как в веществе возникает намагниченность навстречу действующему на него полю, рассмотрим с позиций классической физики орбитальное движение электрона в магнитном поле .

Известно, что частица массой , движущаяся по круговой орбите радиусомсо скоростью, обладает механическим моментом количества движения

.

В то же время вращение электрона вокруг ядра создает круговой электрический ток и, следовательно,

орбитальное движение электрона, как заряженной частицы, можно охарактеризовать также магнитным моментом

,

который направлен в сторону, противоположную моменту импульса (из-за).

Если плоскость орбиты электрона наклонена к вектору под

углом, то со стороны магнитного поляна электрон действует

отличный от нуля момент силы

,

который, как мы установили, рассматривая поведение витка с

током в магнитном поле, стремится развернуть орбитальный

магнитный момент электрона в направлении поля .

Под действием момента силы (сила Лоренца) момент

импульса будет изменяться.

Найдем изменение момента импульса электрона .

Механический момент количества движения электрона связан с

моментом сил, действующим на электрон в магнитном поле,

уравнением моментов:

.

Следовательно,

и.

Т.к. вектор перпендикулярен плоскости, или, то итакже перпендикулярен этой плоскости.

Поэтому изменение момента импульса орбитального движения электрона можно связать с углом поворота плоскости, иливокруг направления магнитного поля.

Угол называется углом прецессии.

Модуль вектора приращения момента количества движения равен

.

Тогда угол прецессии

,

а угловая скорость прецессии

,

т.к. гиромагнитное отношение для орбитального движения электрона.

Т.е. орбита электрона прецессирует с постоянной угловой скоростью (частотой)

частота ларморовской прецессии.

Т.о., появляется дополнительное вращение как целого системы одинаково заряженных частиц, возникающее при наложении на систему однородного постоянного магнитного поля, направление которого служит осью вращения.

Частота одинакова для всех электронов и не зависит от радиуса орбиты и наклона орбиты к вектору.

Ларморовская частота много меньше частотыорбитального движения электронадаже в очень сильных магнитных полях (,порядковый номер элемента;главное квантовое число).

Теорема Лармора(1857-1942г.г.).

При наличии внешнего постоянного магнитного поля внутреннее движение электронов атома не изменяется, но атом в целом получает дополнительное вращение с угловой скоростью .

Понятно, что угловая скорость ларморовского вращения электронов совпадает по направлению с вектором магнитной индукциии не зависит от направления скорости движения электрона по орбите. Т.о., все орбиты электронов в атоме испытывают одинаковую прецессию.

Ларморовская прецессия, как и любое направленное движение заряженных частиц, связана с переносом электрического заряда и может быть охарактеризована слой эквивалентного кругового тока :

.

Магнитный момент, обусловленный прецессией электронных орбит, может быть представлен как

,

и, поскольку электрон несет отрицательный заряд (),направлен против поля.

Здесь мы ввели средний квадрат радиуса проекции орбиты на плоскость, перпендикулярную направлению магнитного поля.

Т.о., в результате прецессии электронных орбит среда намагничивается, причем характеризующий намагниченность вектор направлен против вызывающего её магнитного поля. Это явление называютдиамагнетизмом.

С ларморовским вращением связана дополнительная кинетическая энергия атома. В то же время магнитные силы не могут сообщить атому ларморовское вращение, т.к. они перпендикулярны скорости электрона и поэтому работы не производят. Поэтому магнитные силы способны только поддерживать, но не создавать ларморовское вращение. Это движение возникает во время включения магнитного поля и является одним из проявлений электромагнитной индукции(см. Приложение 3).

3.11.2. Диамагнитная восприимчивость и проницаемость.

Рассчитаем диамагнитные восприимчивость и проницаемость вещества. Момент импульса электрона, обусловленный прецессией, , тогда соответствующий ему магнитный момент можно получить, используя гиромагнитное отношение:

.

Чтобы найти наведенный магнитный момент атома, надо просуммировать вклад всех его электронов.

Средний квадрат радиуса проекции орбиты электрона на плоскость, перпендикулярную полю , определяющий магнитный момент ларморовской прецессии, равен.

Расстояние электрона до ядра атома (радиус орбиты) определяется выражением . Полагая, что электроны в атоме распределены сферически симметрично, можем записать

.

Если в атоме электронов, то его средний магнитный момент, обусловленный ларморовской прецессией в магнитном поле

,

где .

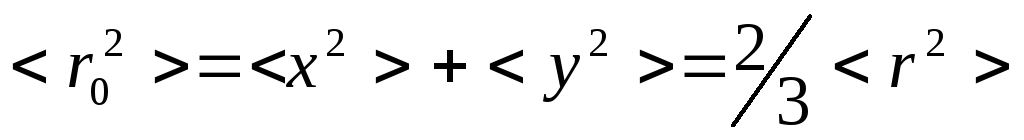Замена напроизведена в связи с тем, что для диамагнетиков разница между этими величинами пренебрежимо мала.

Тогда, если число атомов в единице объема вещества, то вектор намагничивания равен:

.

Из выражения находим магнитную восприимчивость

(в СИ:)

и магнитная проницаемость материала:

Т.е. имеем ;.

Энергия теплового движения слишком мала, чтобы изменить внутреннее движение в атоме. Поэтому восприимчивость и проницаемость диамагнетиков не должны зависеть от температуры. Этот вывод находится в согласии с опытом.

В заключение параграфа еще раз подчеркнем, что диамагнетизм есть универсальное явление, присущее всем средам. Однако в тех случаях, когда атомы обладают собственными магнитными моментами, диамагнитный эффект перекрывается значительно более сильным парамагнитным эффектом.