8

Электромагнетизм

Глава 3. Электрический ток.

1. Уравнение непрерывности. Время релаксации.

1. Ток и плотность тока. Опытные законы.

Под электрическим током понимают перенос заряда через некоторую поверхность , например, поперечное сечение проводника. Количественно перенос заряда характеризуют силой тока , которую определяют как заряд, проходящий через поверхность в единицу времени: .

Единица силы тока в СИ – ампер соответствует переносу заряда в один кулон за одну секунду, что эквивалентно 6,2 ^. 10¹⁸ электронов/сек.

Ампер равен силе неизменяющегося тока, который при прохождении по двум параллельным, прямолинейным проводникам бесконечной длины и ничтожно малого сечения, расположенным в вакууме на расстоянии 1 м один от другого, вызвал бы на участке проводника, длиной 1 м, силу взаимодействия, равную 2^.10^-7 Н.

Следует четко понимать, что, когда мы говорим об электрическом токе, то всегда имеем в виду перенос полного заряда с учетом знаков носителей. Например, движение нейтрального тела связано с переносом заряда впечатляющей величины – около 10⁵ кулонов на грамм вещества. Однако электрического тока мы при этом, естественно, не наблюдаем, т.к. перемещается в точности одинаковое число положительных и отрицательных элементарных частиц (носителей электрического заряда) с совершенно одинаковой средней скоростью.

В этой главе мы ограничимся рассмотрением тока проводимости в проводящих средах. Отметим, что в металлах и полупроводниках носителями тока являются электроны, в электролитах и ионизованных газах – положительные и отрицательные ионы и электроны.

Опыт Толмена и Стюарта.

Предположение о том, что в металлах носителями тока являются свободные, т.е. сравнительно слабо связанные с ионами кристаллической решетки электроны, было проверено экспериментально.

Рике в течение года пропускал электрический ток через поставленные друг на друга медный, алюминиевый и снова медный цилиндры для определения носителей электрического заряда. Если бы в переносе электрического заряда в металлах участвовали ионы, то электрический ток сопровождался бы электролизом и связанным с ним переносом вещества. Общий заряд, прошедший через эту систему составил 3,5 миллиона кулонов, однако никакого проникновения металлов друг в друга обнаружено не было, и вес цилиндров сохранился с точностью до 0,03 мг. Это позволяет утверждать, что ионы в металлах не участвуют в переносе электричества.

Еще более определенное заключение о природе носителей тока в металлах дают возможность сделать опыты с возбуждением электрического тока силами инерции. В опытах Толмена и Стюарта (1916 г.) катушки из металлической (медной, алюминиевой и серебряной) проволок, длиной до 500 м, приводились в быстрое вращение (линейная скорость достигала 300 м/с) вокруг своей оси. Концы проволочной обмотки были соединены с очень чувствительным баллистическим гальванометром длинными гибкими проводами, скручивающимися во время вращения катушки. Магнитное поле Земли при помощи специальных неподвижных катушек, по которым пропускался электрический ток, было настолько тщательно скомпенсировано, что во вращающейся с постоянной угловой скоростью катушке гальванометр не обнаруживал никаких индукционных токов. Убедившись в этом, экспериментаторы быстро затормаживали вращение катушки, тогда гальванометр тотчас же отклонялся.

Интерпретировался полученный результат с помощью следующей модели. Поскольку свободные электроны слабо связаны с решеткой, то при ускорении вращения, они будут отставать, а при замедлении – опережать ионы кристаллической решетки. Т.о. возникнет движение электронов относительно кристаллической решетки, т.е. электрический ток. Для количественного описания наблюдаемого явления можно выбрать систему отсчета, вращающуюся вместе с катушкой. В этой системе отсчета появляется сила инерции, действующая на каждый свободный электрон. Отношение этой силы к заряду электрона и определяет электрическое поле, возбуждающее электрический ток.

Опуская математические выкладки (Сивухин, т.III, стр.435-436), сразу запишем, что количество электричества, протекшего через гальванометр, описывается уравнением

, (1.1)

если - длина проволоки в катушке; - линейная скорость вращения; - общее сопротивление цепи.

Измерив с помощью гальванометра величину , из уравнения (1.1) можно определить удельный заряд носителя электричества , что и было сделано. В пределах ошибок измерений он оказался таким же, как и у электронов в опытах с катодными лучами. Направление отклонения гальванометра показало, что носителями тока в металлах являются отрицательные заряды.

Плотность электрического тока.

В отсутствие электрического поля носители тока совершают хаотическое движение, и через любую воображаемую поверхность проходит в обе стороны в среднем одинаковое число носителей того и другого знака, так что ток через поверхность равен нулю. При включении электрического поля на хаотическое движение носителей накладывается упорядоченное движение с некоторой средней скоростью и через поверхность появляется ток. Скорость называют дрейфовой скоростью, или скоростью дрейфа носителей тока.

Рассмотрим сначала простейший случай, когда все носители тока одинаковы, например, электроны в металлах.

Выделим мысленно в среде, по которой течет ток, произвольный физически бесконечно малый объем (объем, содержащий большое число атомов, но имеющий размеры во много раз меньше, чем те расстояния, на которых свойства среды заметно меняются). Пусть вектор - скорость дрейфа носителей в рассматриваемом объеме. Обозначим через концентрацию носителей тока, т.е. их число в единице объема. Проведем теперь бесконечно малую площадку , перпендикулярную скорости , и построим на ней бесконечно короткий прямой цилиндр высотой .

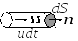
Частицы, заключенные внутри этого цилиндра, за время пройдут через площадку , перенеся через нее в направлении вектора заряд

,

где - заряд отдельной частицы (в металле – электрона). Тогда через единицу площади поверхности в единицу времени протекает электрический заряд

, или . (1.2)

Вектор называется плотностью электрического тока. По величине плотность тока есть заряд, переносимый в единицу времени через единичную площадку, перпендикулярную току. Направление вектора совпадает с направлением упорядоченного течения положительного электричества.

Ток в длинном проводнике, например в проволоке, равен, разумеется, интегралу от плотности тока по поперечному сечению проволоки. Действительно, ток , протекающий через некоторую поверхность , равен поверхностному интегралу

. (1.3)

Т.о. есть поток вектора . Заметим, что используемая терминология в данном случае весьма удачна (физична).

Обобщение проведенных рассуждений на случай нескольких типов зарядов, создающих ток, не представляет труда.

, (1.4)

где суммирование ведется по всем типам носителей тока.

Вообще, количество переносимого электричества можно записать в виде

.

Последняя формула остается верной и в том случае, когда площадка не перпендикулярна вектору .

Положительное направление нормали к площадке устанавливается

произвольно. Если положительные частицы движутся в направлении нормали , то

переносимый заряд будет положительным. При движении тех же частиц в

противоположном направлении переносимый заряд отрицателен. Для отрицательных

частиц это картина будет обратной.

Основные законы электрического тока. Закон Ома и закон Джоуля-Ленца.

1. Закон Ома для участка цепи.

Создание и поддержание в веществе электрического поля является одним из основных способов возбуждения электрического тока. Как показывает опыт, для многих тел в широких пределах справедливо соотношение

, или. (1.5)

Последнее выражение можно переписать в дифференциальном виде

,

.

. (1.6)

Полученное выражение носит название закон Ома в дифференциальной форме,

где - удельная проводимость или электропроводность, зависящая от физического состояния тела (температуры, давления и т.д.);

величина, обратная электропроводности, называется удельным сопротивлением материала.

2. Закон Джоуля-Ленца.

Энергия, выделяемая при прохождении электрического тока на участке цепи, равна

. (1.7)

В дифференциальной форме

,

. (1.8)

Уравнения (1.7) и (1.8) выражают закон Джоуля-Ленца, соответственно, в интегральной и дифференциальной формах.

2. Закон сохранения электрического заряда.

Одним из фундаментальных законов электричества является закон сохранения электрического заряда, установленный в результате обобщения опытных фактов. Придадим ему математическое выражение, связав с такими макроскопическими величинами, как плотность заряда и плотность электрического тока .

Возьмем в проводящей среде произвольную замкнутую поверхность , ограничивающую некоторый объем . Количество электричества, ежесекундно вытекающее из объема через поверхность ,

выражается интегралом . С другой стороны, убыль заряда в объеме можно

представить в виде , где - заряд, содержащийся в объеме . Если закон

сохранения заряда выполняется, приравнивая эти выражения, получаем

. (1.9)

Представив заряд, находящийся в рассматриваемом объеме как

и воспользовавшись теоремой Гаусса-Остроградского

,

получаем

. (1.10)

Поскольку это уравнение записано для произвольного объема, то равенство справедливо также и для подынтегральных выражений:

. (1.11)

Это и есть уравнение непрерывности, или уравнение неразрывности, выражающее закон сохранения электрического заряда.

Если вектор плотности тока с течением времени повсюду остается постоянным, то говорят, что мы имеем дело с системой стационарных токов. Стационарные токи удовлетворяют закону сохранения заряда.

, то или . (1.12)

Заметим, что знак частной производной используется в связи с тем, что , вообще говоря, зависит как от времени, так и от пространственных координат.

3. Максвелловское время релаксации.

Если в проводящей среде по какой-либо причине нарушено равновесие электрических зарядов, то возникает электрический ток, характеризуемый плотностью и направленный таким образом, чтобы восстановить равновесное распределение зарядов в проводнике. Величиной, характеризующей время прохода системы к равновесию, служит время релаксации (максвелловское).

; ;

; ; ;

- время релаксации. В проводящих средах эта величина составляет .