2. Расчет дальности связи по методике eurocost

Европейское Объединение для Научных и Технических Исследований (EURОCOST) сформировало рабочий комитет COST-231, установивший Европейский стандарт расчета дальности радиосвязи на частотах до 2 ГГц.

Основой методики расчета является модель Хата. В основе этой модели лежат зависимости среднего ослабления напряженности поля в городских условиях относительно напряженности поля в свободном пространстве в зависимости от рабочей частоты при расстоянии между радиостанциями как параметре. Согласно этой модели производится расчет дальности радиосвязи в свободном пространстве, а затем вычисляется поправочный коэффициент L для 5.1, отражающий параметры реальной радиолинии. Наиболее эффективно применение модели Хата для расчета УКВ радиолиний в городских условиях в диапазоне частот от 150 до 1500 МГц.

Величина потерь распространения в реальной радиолинии определяется по формуле:

5.4

Коэффициент определяется из следующих уравнений:

• Для маленьких городов

5.5.a

• Для больших городов на частотах менее 300 мГц:

5.5.b

• Для больших городов на частотах более 300 мГц:

5.5.c

Для расчета потерь в пригородной зоне основная формула модифицируется следующим образом:

5.5.d

Для расчетов потерь за городом (практически открытое пространство) основная формула модифицируется следующим образом:

5.5.e

Расчеты по формулам 5.4, 5.5 справедливы при следующих ограничениях:

Частота ________________________________________

Высота передающей антенны ______________________

Высота приемной антенны ________________________

Расстояние между приемником и передатчиком ­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­______

После предварительного расчета дальности радиосвязи по классической формуле для свободного пространства 5.1 вычисленная дальность корректируется в соответствии с расчетами по 5.4, 5.5.

Расчет дальности, в основе которого лежат рекомендации EUROCOST, рекомендован для использования в стандарте транкинговой связи TETRA. Этот стандарт рекомендует несколько вариантов реализации модели Хата в зависимости от конкретных условий местности и типа застройки.

3. Расчет теневых зон радиосвязи

Три основных механизма составляют основу классической теории распространения радиоволн: отражение, рассеяние, дифракция.

Все эти три эффекта в усредненном, вероятностном представлении учитываются в эмпирических коэффициентах расчетных формул 5.1 ... 5.5. Дальность радиосвязи, рассчитанная согласно этим формулам, имеет усредненный, вероятностный характер.

Для уточненного расчета зон радиотени от больших протяженных объектов используются известные в теории дифракции формулы зон Френеля. Явление дифракции объясняется на основании эффекта Гюйгенса, согласно которому любая точка фронта распространения волны может рассматриваться как источник вторичных радиоволн, которые, в свою очередь, распространяются во всех возможным направлениях. Дифракция позволяет УКВ радиосигналам распространяться за горизонт и определяет структуру поля за препятствием.

Дифракционные эффекты позволяет, с некоторой вероятностью, осуществлять связь на УКВ частотах за горизонтом, вне прямой видимости передатчика и приемника. Однако реального, практического значения это не имеет. Современные методики построения сетей связи направлены, прежде всего, на обеспечение уверенной радиосвязи в любой точке зоны покрытия. Это предполагает получение избыточно высокого уровня передаваемой мощности всюду в зоне покрытия и, поэтому, возможность неустойчивой загоризонтной связи просто игнорируется.

Совсем иное дело расчет поля за препятствием. При чисто геометрическом рассмотрении электромагнитное поле за большим препятствием отсутствует, если препятствие много больше длины волны. Однако реально напряженность поля за препятствием есть и вполне достаточная для нормального приема радиосигналов. Точный расчет напряженности поля за большими препятствиями всегда проводится при выборе и оптимизации расположения базовых передатчиков в многозоновой сети связи.

В самом простом случае напряженность поля за препятствием определяется в модели Найфа:

5.6

Коэффициент ослабления поля определяется кривой Knife (рис.5.2), рассчитанной как суммарная напряженность поля от всех зон Френеля, и аналитически записывается в следующем виде:

5.7

G, дБ

0

-5

-10

-15

-20

-2 -1 0 1 2

Рис.5.2. Дифракционная зависимость ослабления поля в модели Knife

Параметр v определяется по формуле 5.8, смысл геометрических параметров, входящих в эту формулу, ясен из рисунка 5.3.

5.8

Передатчик

Приемник

d₁ d₂

Рис.5.3. К расчету дифракционного поля за препятствием

4. Распространение радиоволн внутри здания

Все предыдущие формулы для расчета поля в пространстве существенно относятся к открытым объемам. Во всяком случае, бесконечно большим по сравнению с длиной волны. Однако в последние годы активно развиваются персональные системы связи (PCS – Personal Communication Systems). Основное место применения этих систем - внутренние помещения зданий. Соответственно. возникает необходимость в анализе и расчете распространения поля в специфических условиях помещений.

Распространение радиоволн внутри зданий имеет специфические черты, связанные со средой распространения. В отличии от свободного пространства, невозможно для объема внутри здания определить диэлектрическую или магнитную проницаемость среды. Параметры среды распространения меняются очень сильно на очень небольших расстояниях, как, например, при междуэтажном распространении. Применение некоторых «усредненных» параметров в настоящее время не находит теоретического обоснования.

В результате, распространение радиоволн в зданиях очень сильно зависит от таких специфических характеристик, как тип конструкционного материала здания, наличие в стенах здания металла, количества этажей в здании, плотность размещения оборудования в здании и т.п.

Механизмы, определяющие распространение радиоволн в здании в приближении «больших расстояний» те же самые, что и пространственного распространения – дифракция, отражение, рассеяние. Следует ясно понимать, что, не смотря на небольшие расстояния дальности персональной радиосвязи в здании, применение моделей «распространения радиоволн» принципиально означает расчет поля на расстояниях, много больших длины волны и игнорирование явлений интерференции переотраженных волн.

В настоящее время экспериментальные данные по измерениям дальности радиосвязи внутри здания являются основным источником информации при проектировании систем связи. Многие фирмы, выпускающие оборудование персональной радиосвязи, проводят и публикуют результаты измерений затухания напряженности поля в радиоканале по сравнению с расчетным значением поля в свободном пространстве. При этом различие в публикуемых данных очень велико. Например, «результаты измерения затухания радиоволн в большом универсаме» по разным источникам могут отличаться на 10 дБ. Потому, что универсамы разные.

Разумеется, ценность таких измерений как основание для общих выводов очень невелика. Однако реально это единственный надежный источник информации для хотя бы примерной оценки необходимой мощности передатчиков в системе связи.

Одним из типичных вариантов полуэмпирической формулы для расчета затухания радиоволн в здании является следующая зависимость:

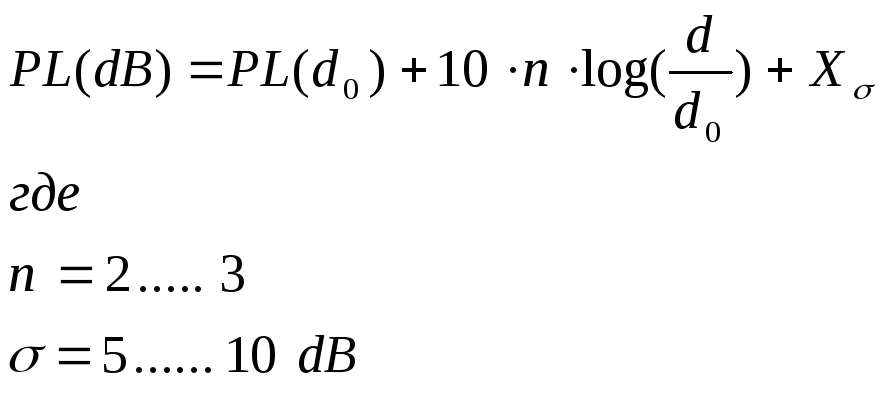5.9

Дисперсия ошибки при расчете по формуле 5.9 достигает 13 дБ. Некоторые измерения показывают, что точность расчетов по 5.9 увеличивается (дисперсия ошибки менее 5 дБ), если в формулу добавить еще один член, экспоненциально увеличивающийся с расстоянием:

5.10

Фирма Эрикссон в своих расчетах использует графическое представление для определения величины затухания поля в зависимости от расстояния (рис.5.4).

Напряженность поля внутри здания от внешнего передатчика имеет важное значение для систем связи. Как и в случае измерений междуэтажного затухания, трудно определить точную модель наведенного внешним источником поля. Количество опубликованных экспериментальных данных невелико и их трудно сравнивать. Однако некоторые обобщения все-таки можно сделать.

дБ

30

50

70

90

110

1 3 10 20 40 100 м

Рис.5.4 Графическая модель Эрикссона для затухания поля внутри здания

1. Напряженность наведенного поля внутри здания повышается с высотой, на нижних этажах наблюдается большее затухание поля. Уменьшение потерь поля происходит со скоростью примерно 1.9 дБ/на этаж от первого до четырнадцатого этажа. На более высоких этажах потери проникновения поля вновь увеличиваются. Номер этажа, начиная с которого происходит увеличение потерь, зависит от близости окружающих зданий. Чем ближе другое здание, тем на более низком этаже (зафиксирован девятый этаж) потери начинают увеличиваться.

2. Напряженность наведенного поля увеличивается с ростом частоты. Измерения, проведенные на первом этаже здания, показали следующие результаты:

Потери (дБ)	Частота (МГц)
-16.4	440
-11.6	890
-7.6	1400

В то же время измерения напряженности поля около открытого окна не показали существенного изменения поля с частотой: разница в принимаемом сигнале 1.5 дБ при изменении частоты от 900 до 2300 МГц при среднем ослаблении –6 дБ.

3. Расчет распределения поля в модели «малого расстояния»

Основное, самое характерное отличие распространения сигналов в городских условиях от распространения сигналов в свободном пространстве или при наличии отдельных отражающих поверхностей заключается в эффекте многолучевого распространения при нестационарных граничных условиях.

Плотная городская застройка с точки зрения электродинамики характеризуется как огромное количество отражающих поверхностей, так что сигнал передатчика достигает приемника несколькими различными путями. Очень частот прямая видимость между передатчиком и приемников вообще отсутствует и на антенне приемника действует одновременно несколько копий сигнала с примерно равными амплитудами.

Различают три наиболее существенных эффекта, к которым приводит многолучевое распространение в радиоканале, а именно:

• Быстрые изменения напряженности поля на небольшом расстоянии или в течении короткого времени (фединг)

• Случайная угловая модуляция несущей вследствие изменения доплеровского сдвига для различных копий сигнала

• Временная дисперсия (эхо), вызванное различным временем распространения копий сигнал от передатчика к антенне.

Среди различных эффектов многолучевого распространения фединг в наибольшей степени влияет на возможность приема сигнала и качество принимаемой информации. Постоянное изменение расстояния между приемником и передатчиком, а также изменение положения препятствий (движение транспорта) приводит к постоянным изменениям амплитуды копий сигнала, приходящих в точку приема. Измерения в городских условиях показывают, что разница между максимальным и минимальным значением интерференционного поля достигает 30 дБ, а изменение напряженности поля в 15 дБ на расстоянии менее 1м не редкость.

Кроме амплитудный флуктуаций, постоянное изменение расстояния между абонентами приводит к изменению времени распространения копий, т.е. к постоянному изменению фазы принимаемого сигнала. Возникающая паразитная фазовая модуляция зависит как от параметров распространения, так и частоты сигнала.

Движение абонента с переменной скоростью и под произвольными углами по отношению к базовой радиостанции приводит возникновению случайного доплеровского сдвига частоты несущей, т.е. к возникновению паразитной частотной модуляции.

Таким образом, излучаемый передатчиком сигнал с постоянной амплитудой и фазой приходит на приемник как сигнал с паразитной амплитудной и угловой модуляцией.

Рассматриваемые ниже модели «малого расстояния» и позволяют определить основные характеристики электромагнитного поля в условиях нестационарных многократных отражений. Основой моделей «малого расстояния» является представление канала распространения в виде некоторого паразитного узкополосного модулятора. Этот модулятор, очевидно, описывается комплексной огибающей, характеризующей возникающую в процессе многолучевого распространения амплитудную, фазовую и частотную модуляции. Нестационарность процесса модуляции в канале распространения отражается зависимостью параметров комплексной огибающей канала от времени.

1. Представление принимаемого сигнала в многолучевом канале

Высокочастотный модулированный сигнал , излучаемый передатчиком в эфир, очевидно представляется через свою комплексную огибающую :

5.11

Многолучевой канал распространения, рассматриваемый как паразитный модулятор, вносит дополнительную амплитудную и фазовую модуляции в передаваемый сигнал. Следовательно, принимаемый сигнал на входе приемника может быть представлен в виде:

5.12

Комплексная огибающая в общем случае приема N копий сигнала может быть записана в следующем виде:

5.13

Амплитуда комплексной огибающей отражает переменную амплитуду принимаемой к-ой копии высокочастотного сигнала вследствие изменения со временем потерь распространения в канале.

Фаза комплексной огибающей отражает изменение со временем фазы несущей частоты для к-ой копии сигнала вследствие изменения времени распространения к-ой копии сигнала от передатчика к приемнику.

Задержка комплексной огибающей отражает различное время распространения копий высокочастотного сигнала от передатчика к приемнику.

Для описания параметров многолучевого канала удобно использовать временной элемент разрешения (дискретизации) и все возможные задержки прихода копий сигнала обозначать через , где расстояние между двумя любыми соседними и равно , а обозначает максимально возможную задержку прихода копии сигнала. Время распространения первой копии от передатчика до приемника не учитывается и начальное значение . Несколько возможных копий внутри одного временного интервала рассматриваются как одна копия.

2. Энергия принимаемого сигнала в многолучевом радиоканале

Очевидно, что суммарный baseband сигнал на входе приемника в многолучевом канале имеет вид:

5.14

Предполагается, входной сигнал квазистационарный, т.е. в интервале времени от 0 до параметры канала распространения неизменны, амплитуды и фазы приходящих копий не изменяются. В каждый момент времени имеет место приход на вход приемника очередной копии основного сигнала. Очевидно, что не все копии в каждый данный момент присутствуют, т.е. вполне возможно для некоторых .

Рассмотрим выражение 5.14 для двух крайних случаев: передача сигнала с амплитудно импульсной модуляцией РАМ при малой длительности импульсов, так что , и РАМ сигнал с импульсами очень большой длительности, так что . В обоих случаях период повторения импульсов значительно больше, чем максимально возможная задержка копий в многолучевом сигнале, т.е. .

Определим суммарную энергию принятого сигнала с учетом всех возможных копий.

Как было определено ранее, энергия принимаемого сигнала равна интегралу от квадрата модуля baseband сигнала по времени длительности сигнала. В 5.15 использована -функция для обозначения короткого времени существования амплитуды принимаемого сигнала в начале каждого временного интервала . Таким образом, возведение в квадрат суммы N слагаемых сводится к возведению в квадрат каждого отдельного слагаемого, (различные копии принимаемого сигнала не существуют в одно и то же время). Интегрирование, вследствие наличия -функции сводится к умножению подинтегрального выражения в момент времени на общий интервал интегрирования.

5.15

Главный вывод из формулы 5.15 – при распространении модулированного сигнала с длительностью импульсов, меньших минимального времени прихода копии сигнала (меньших времени разрешения приемником отдельных копий), суммарная энергия принятого сигнала равна сумме энергий каждой копии сигнала.

Обратная величина от длительности импульса модулированного сигнала характеризует полосу частот, занимаемую модулированным сигналом. Обратная величина от минимального времени задержки прихода копии сигнала характеризует полосу частот канала. Следовательно, в узкополосном канале (узкополосном по сравнению с полосой модулированного сигнала) все копии принимаются независимо друг от друга.

При воздействии сигнала с длительностью больше выражение для энергии принимаемого сигнала имеет следующий вид:

5.16

Амплитуда передаваемого сигнала постоянна за все время прихода копий и вынесена из под интеграла.

Как следует из 5.16, при приеме модулированного сигнала с длинными (по отношению ко времени задержки прихода копий) импульсами суммарная энергия принимаемого сигнала зависит не только от амплитуд копий, но и от их взаимной фазировки. Иначе можно сказать. что в широкополосном канале суммарная энергия принимаемого сигнала определяется и амплитудами, и фазами приходящих копий сигнала.

Очевидно, что при взаимном движении приемника, передатчика или отражающих объектов амплитуды копий сигналов меняются не очень существенно. Величина затухания сигнала при перемещении приемника, например, на 8 см практически не изменится. Следовательно, амплитуда принимаемого широкополосного сигнала изменяется медленно и плавно при перемещении абонента.

И наоборот, изменение фазы приходящей копии сигнала очень существенно даже при небольших перемещениях. Например, для частоты 900 МГц изменение фазы на расстоянии 8 см равно 90 градусов. Следовательно, мощность принимаемого узкополосного сигнала испытывает быстрые и глубокие изменения при движении абонента.