ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 16

Коэффициент бокового давления грунта и методы его определения. Зависимость Герсеванова между коэффициентом Пуассона и коэффициентом бокового давления.

ε_x= ε_y=0(поперечные, боковые деформации невозможны). В этом случае отношение сжимающих поперечных напряжений σ_x= σ_y к действующему напряжению σ_z называют коэффициентом бокового давления ξ, т.е ξ= σ_х/ σ_z= σ_y/ σ_z. Долгие годы методы определения коэффициента ξ базировались на использовании компрессионного прибора, позднее стали применять приборы трехосного сжатия- стабилометры. Первым ‘’компрессионным’’ методом был предложен ‘’метод ленты’’(К. Терцаги). В этом методе помещенная в компрессионный прибор тонкая стальная лента вытягивается усилием Т, которое замеряется. Для определения ξ выполняют два опыта: в одном опыте лента размещается в грунте горизонтально и усилие вытягивания составит Тг=2 σ_zАf, в другом опыте- вертикально и усилие Тв=2 σ_z ξ Аf, где А, f-площадь ленты и коэффициент трения грунта по ленте. По результатам замера усилий Тв, Тг получаем ξ=Тв/Тг. Позднее ξ стали определять, замеряя давление (σ_x, σ_y) на внутреннюю поверхность кольца компрессионного прибора, устанавливая в кольце чувствительный датчик давления. Существенным недостатком этого метода является невозможность выполнения условия ε_x= ε_y=0 для грунта, контактирующего с мембраной датчика, ибо оценка давления основана на замере прогиба мембраны, который не может быть в этом случае нулевым. Применением “жесткой” мембраны с высокоточным методом измерения ее малых прогибов удается весьма точно определять значение ξ. Коэффициент Пуассона ν= lε_xl/ ε_z= lε_yl/ ε_z(отношение поперечных и продольных деформаций в условиях одноосного растяжения или сжатия без ограничения боковых деформаций). В этих условиях экспериментально определяют ν для многих конструкционных материалов(металла, бетона и пр.), а также для скальных грунтов, глинистых грунтов твердой консистенции и др. Для малосвязных и несвязных грунта такое определение невозможно и поэтому обычно используется связь между ν и ξ. Связь между ν и ξ для грунта можно установить, принимая для него модель ЛДС с использованием физ-х урав-й обобщенного закона Гука для ε_x и ε_y в условиях компрессионного опыта. В результате получаем (Н.М.Герсеванов) ν= ξ / (ξ+1) или ξ = ν /(1- ν). Т. О по экспериментально найденному ξ мы можем найти коэф. Пуассона.

Определение осадок при учете боковых деформаций. Определение осадки по теории упругости (формула Шлейхера). Полевые методы определения модуля деформации грунта основания.

В этом способе зависимость для ε_z принимается как в виде (ε_z=1/Е(σ_z- ν (σ_х +σ_y)), так и в другой, эквивалентной форме. В частности при добавлении и вычитании в правой части величины νσ_z/Е, получаем для ξ_z выражение (ε_z=1/Е(σ_z (1 + ν)- νθ), где θ= σ_x+ σ_y+ σ_z). В свою очередь можно записать в виде: (ε_z=(1+ ν )/Е(σ_z -θ /3)+( (1 - 2ν) /Е)θ. Учитывая выражение для объемной деформации ε _ν=(1-2 ν)θ/Е и зависимость ε _ν=(е₁-е₂) /(1+е₁), в результате:( (ε_z= (((1+ ν )/ (1 - 2ν)) *(σ_z/ θ -1 /3)+1/3) (( е₁-е₂) /(1+е₁)). Любым из выражений можно пользоваться при определении осадок r,s,s+d с учетом боковых деформаций грунта.

Это определение базируется на непосредственном использовании формул (решений) линейной теории упругости(ЛТУ) для вертикальных перемещений “точек” (элементарных объемов) на поверхности и внутри основания. В практических расчетах обычно приходится определять вертикальное перемещение(осадку) точек вертикали, проходящей через центр площади загружения, т.е величину W(0,0,z)=W(z). Формулы для W от различных распределенных нагрузок принято записывать единым выражением в виде W(z)=(qb(1- ν²)/E)K(z), где b-ширина площади загружения, K(z)-функция положения точки z , определяемая из решения соответствующей задачи теории упругости. Для определения осадки используют выражение s= W(0)-W(z=Ha)= (qb(1- ν²)/E)(K(0)- K(Ha))= (qb(1- ν²)/E)K.объединяя эту зависимость для различных вариантов площади загружения и жесткости фундамента(штампа), передающего давление на основание, в практике расчетов используют формулу Шлейхера:(s=((1- ν²)/E)pbw) в ней: p-среднее давление под фундаментом, b-ширина фундаента, w- коэф. Учитывающий форму площади загружения и жесткость фундамента.

В полевых условиях: модуль деформации определяют испытанием грунта статической нагрузкой, передаваемой на штамп. Испытания проводят в шурфах жестким круглым штампом площадью 5000 см² , а ниже уровня грунтовых вод и на больших глубинах- в скважинах штампом площадью 600 см² ..При испытании грунтов необходимо, чтобы толщина слоя однородного грунта под штампом была не менее двух диаметров штампа. Модули деформации изотропных грунтов можно определять в скважинах с помощью прессиометра. В результате испытаний получают график зависимости приращения радиуса скважины от давления на ее стенки .Модуль деформации вычисляют по формуле Е= kr₀Δp/ Δr, к определяют путем сопоставления данных прессиометрии с результатами параллельно проводимых испытаний того же грунта штампом.

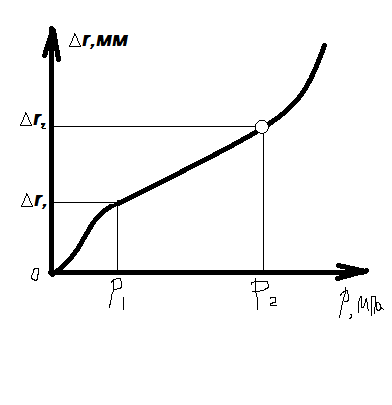
Зависимости осадки

основания s от нагрузки q по решению

теории упругости (1), по упругопластическому решению и

согласно результатам штамповых испытаний (2).

Зависимость деф. Стенок от давления

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 15

Сжимаемость грунтов при статических нагрузках. Компрессионный прибор и напряженно-деформированное состояние образца грунта в нем. Кривые уплотнения, разбухания и их характеристики.

При действии нормальных сжимающих напряжений дисперсные грунты получают деформацию уплотнения, которая характеризует одно из основных свойств грунта – его сжимаемость.

В лабораторных условиях деформируемость (сжимаемость) дисперсных грунтов обычно исследуют в условиях невозможности бокового расширения грунта (ε_х=ε_у=0), проводя испытания в приборах, называемых компрессионными (рис.2.1,а). Образец грунта 1 помещают в жесткое кольцо (обойму) 2 и к нему через жесткий штамп 3 прикладывают вертикальное сжимающее напряжение σ = Р/А (А – площадь горизонтального сечения образца, обычно А = 40 см² при d = 7,07 см). Для уменьшения сил трения грунта о стенки кольца диаметр образца d в 3…4 раза больше его высоты (h ≈ 2,0 см). В процессе сжатия водонасыщенного грунта из его пор выдавливается вода, поэтому в основании прибора и в штампе устраивают фильтры 4 в виде перфорированных пластинок для отвода воды. Через отверстия в штампе может осуществляться, при необходимости, транзитная нисходящая или восходящая фильтрация воды через образец грунта.

Уравнение спрямленного участка ветви компрессии имеет вид: е = - аσ + b, где а и b - параметры прямой. Как следует из рис.2.2,а параметр b - отрезок, отсекаемый прямой на оси е, а величина параметра а, называемого коэффициентом уплотнения (сжимаемости), определяется как а = (е₁-е₂)/(σ’’-σ ‘), и имеет размерность, обратную напряжению 1/Мпа,см²/кгс.

При уменьшении сжимающих напряжений σ, т.е. разгрузке грунта, наблюдается увеличение коэффициента пористости и объема грунта, т.е. имеет место разбухание (разуплотнение) грунта; получаемый при этом график 2 (рис.2.2,б) называют кривой декомпрессии (кривой или ветвью разуплотнения). Коэффициент разбухания определяется как а_р = (е₂-е₁)/(σ’-σ ‘’)

При увеличении напряжений от σ^// (рис.2.2,б) получаем ветвь вторичного нагружения – кривую рекомпрессии 3, которая с кривой разбухания 2 образует петлю гистерезиса, при этом при восстановлении напряжения σ^/ коэффициент пористости е₂ ^/ получается меньше е₂. Характерно, что при дальнейшем увеличении напряжений (σ > σ^/) кривая нагружения грунта получает больший уклон и выходит на ветвь первичного уплотнения, иногда называемую главной или основной ветвью уплотнения (компрессии).

Рис. 2.1. Схема компрессионного прибора (а) и зависимость относительного сжатия грунта от вертикального напряжения (б): 1- грунт, 2 - кольцо, 3 –поршень-штамп, 4 - фильтр, 5,6 - опытные зависимости при нагружении и разгрузке.

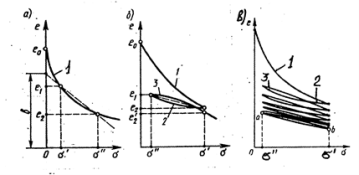
Рис. 2.2. Зависимости коэффициента пористости от напряжения в компрессионном испытании при нагружении, разгрузке, повторном нагружении (кривые 1, 2,3) и при циклической нагрузке и разгрузке

Определение напряжений по подошве сооружений конечной жесткости (допущения, дифуравнение изгиба полосы и используемые модели основания). Области применения методов коэффициента постели и теории упругости.

В основу большинства контактных задач для сооружений конечной жесткости принимают два существенных допущения, упрощающих решение задач:

1. При деформациях основания и полосы (сооружения) не образуется щели между ними, т.е. Wп(x) = W₀(x) = W(x),где Wп(x),W₀(x) – прогиб полосы и осадка основания. 2. Для изгибаемой полосы допустима гипотеза плоских сечений и соот-ветственно дифференциальное уравнение изогнутой оси, применяемое в курсе сопротивления материалов в виде DW’’(x) = M(x) или, учитывая, что M’’= Q’ = q(x) = f(x) – φ(x) (рис. 4.1,а), получаем DW^IV(x) = f(x) – φ(x)(4.15),где D — цилиндрическая жесткость полосы, D = Е_пI_п/(1 – ν²_п), Е_п, ν_п — модуль упругости и коэффициент Пуассона материала полосы; I_п — момент инерции поперечного сечения b_п·h_п = 1·h_п полосы, I_п = (1*h³_п)/12 ; f(x) — интенсивность внешней распределенной нагрузки; φ(x) — интенсивность реакции основания.

Модель коэффициента постели предполагает между W(x) и φ(x) зависимость φ(x) = b*k *W(x). В рез-те получаем дифференциальное уравнение изогнутой оси полосы в виде DW^IV+ b*k *W = f(x) или W^IV+4α⁴W = F(x),

где α=((b*k)/(4D) )^(1/4) и F(x) =f(x)/D .

Модель линейно-деформируемого основания предполагает между φ(x) и W(x) зависимоcть в форме( 4.4). Подставляя (4.4) в дифференциальное уравнение (4.15) получаем уравнение относительно φ(x) в виде:

Основным допущением, определяющим область применения той или иной модели, является принятый характер деформирования основания. По модели коэффициента постели осадка возникает только на участке приложения нагрузки и ее величина зависит от величины нагрузки р и не зависит от площади загружения (рис. 4.9,а). По решению теории упругости осадку получают точки поверхности основания далеко за пределами нагрузки при наибольшей величине осадки в середине площади загружения. При этом величина осадки зависит не только от величины нагрузки р, но и от размеров площади (полосы) загружения (рис. 4.9,б). применение модели коэффициента постели является наиболее обоснованным в случае оснований, представленных грунтами с малыми значениями , с («слабыми» грунтами), а также в случаях сооружений с малой глубиной заложения, малой шириной подошвы и большой нагрузкой на основание, отвечающих развитию значительных пластических областей в основании.

Рис. 4.9. Характер осадки основания по модели

коэффициента постели (а) и теории упругости (б).

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 14

Газообразная фаза в грунтах – свободный и защемленный газ. Влияние защемленного газа на поведение грунта.

В самых верхних слоях грунта газообразная составляющая представлена атмосферным воздухом, в глубоких слоях — азотом, метаном, сероводородом и другими газами и при обязательном наличии в обоих случаях некоторого количества водяного пара. Газ в грунте обычно присутствует в свободном состоянии и частично растворен в воде. Свободный газ подразделяют на не защемленный, сообщающийся с атмосферой, и защемленный, не связанный непосредственно с атмосферой. Не защемленный газ присутствует лишь в пределах глубины 1 — 2 м от поверхности грунта. Ниже весь газ практически защемлен даже выше горизонта грунтовых вод. Даже в водонасыщенном грунте в поровой воде грунта всегда имеется и растворенный газ и защемленный газ в виде пузырьков.

Защемленный газ оказывает наиболее существенное влияние на свойства грунтов и на протекающие в грунтах процессы. Объем пузырь-ков, давление и температура газа в них связаны известным уравнением Клапейрона, в соответствии с которым при уменьшении давления в воде, окружающей пузырек, а также при повышении температуры объем пузырька газа увеличивается. В частном случае постоянной температуры грунта (изотермический режим) связь между объемом пузырька и давлением окружающей воды определяется законом Бойля-Мариотта. Давление внутри пузырька складывается из давления в окружающей воде и давления от поверхностного натяжения воды на контакте с пузырьком. Реально увеличение объема происходит не только вследствие расширения газа в самом пузырьке, но и вследствие выделения в него газа из воды. С повышением давления и понижением температуры поровой воды объем растворенного газа в воде увеличивается. Количественно этот процесс описывается законом Генри V_г = μ_г*V_в, по которому объем растворенного в воде газа V_г пропорционален объему воды V_в и не зависит от величины давления. Коэффициент μг называется коэффициентом растворимости газа. Для воздуха при температуре 0°С μ_г равен 0,0245.