X1, x2,…, xk – экономические переменные.

Фиктивные переменные широко используются для оценки сезонных различий в потреблении. Подробный учет сезонного фактора при построении динамических моделей рассмотрен в главе 8.

Фиктивные переменные могут вводиться не только в линейные, но и в нелинейные модели, приводимые путем преобразований к линейному виду. Так, модель с фиктивными переменными может иметь вид:

,

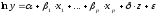где: z – фиктивная переменная.

Целесообразность такого вида модели диктуется характером связи между экономическими переменными:

.

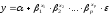Фиктивная переменная вводится в эту модель как очередной сомножитель C^z:

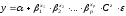
Логарифмируя данное выражение, получим модель:

,

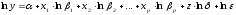которая равносильна приведенной ранее 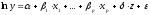, где параметры и случайная составляющая представлены в логарифмах.

До сих пор мы рассматривали фиктивные переменные как факторы, которые используются в регрессионной модели наряду с экономическими переменными. Вместе с тем, возможна регрессия только на фиктивных переменных. Например, изучается дифференциация заработной платы рабочих высокой квалификации по регионам страны. Модель заработной платы может иметь вид:

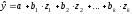
где: y - средняя заработная плата рабочих высокой квалификации по отдельным предприятиям;

;

;

………………………………………………………………………………..

.

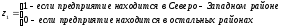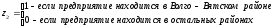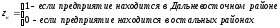Поскольку последний район, указанный в модели, обозначен z_k, то в исследование включено к+1 район.

В виду того, что факторы данной регрессионной модели выражены дихотомическими признаками, параметры модели имеют свою специфику по сравнению с традиционной их интерпретацией. Параметр a представляет собой среднее значение результативного признака для базовой группы 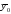. Параметр b характеризует разность средних уровней результативного признака для группы 1 и базовой 0 группы. Соответственно, параметр b_i представляет собой разность между 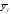и 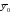. Иными словами, коэффициенты при z отражают величину эффекта соответствующей группы фактора z. Рассмотрим применение данной модели на следующем условном примере.

Таблица 3.5.

Распространенность ручного труда на предприятиях одной отрасли в зависимости от уровня автоматизации производства.

Уровень автоматизации производства	Число заводов	Процент рабочих ручного труда в общей численности рабочих
		на каждом заводе данной группы	в среднем по группе
Высокий	8	31,37,38,39,35,32,34,34	35,0
Средний	12	40,45,47,48,46,48,50,52,39,43,44,56	46,5
Низкий	10	47,54,59,55,57,56,65,57,55,61	56,6
Итого:	30		46,8

По данным этой таблицы рассматривается следующая регрессионная модель:

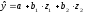
где: y - процент рабочих ручного труда в общей численности рабочих;

z - уровень автоматизации производства,

;

;

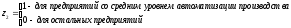В качестве базовой группы, с которой ведется сравнение уровня занятости ручным трудом, выступают предприятия с низким уровнем автоматизации производства.

Модель регрессии, исходя из средних уровней, приведенных в последней графе таблицы 3.5., составит:

.

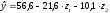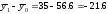Она показывает, что в предприятиях с низким уровнем автоматизации производства средний процент рабочих ручного труда равен 56,6. На предприятиях с высоким уровнем автоматизации производства распространенность ручного труда ниже на 21,6 процентных пункта (), а на предприятиях со средним уровнем автоматизации производства - ниже на 10,1 процентных пункта (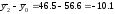) по сравнению с предприятиями третьей группы.

В справедливости данного уравнения регрессии можно убедиться, обратившись к методу наименьших квадратов. Применяя МНК, система нормальных уравнений составит:

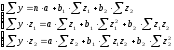
В виду того, что переменные z принимают лишь два значения: 1 или 0, в данной системе имеем следующие равенства:

; ; .

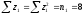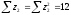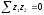Соответственно, система нормальных уравнений составит:

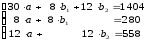
Решая систему, получим: a = 56,6; b₁ = -21.6; b₂ = -10.1. Уравнение регрессии, как было показано ранее, примет вид:

.

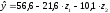Индекс детерминации для данной модели составит:

,

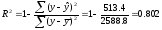что статистически значимо: F-критерий = 54,6; при α = 0,05 и при степенях свободы 2 и 27, F _{табличное} = 3,35.

Поскольку коэффициенты при фиктивных переменных в модели, не содержащей других экономических факторов, характеризуют величину эффектов i-го уровня фактора z, то регрессионная модель по своему содержанию тождественна дисперсионной модели. В основе нашего примера лежит дисперсионная модель вида:

,

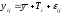где: y_ij – j - ое наблюдение результативного признака на i - ом уровне исследуемого фактора (в примере i =1,2,3; j=1,…,30);

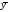- среднее значение результативного признака в целом по совокупности (в примере 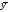= 46,8);

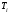- эффект, обусловленный i-ым уровнем фактора;

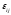- случайная ошибка в j-ом наблюдении на i-ом уровне изучаемого фактора; величина, на которую фактический уровень результативного признака y_ij отличается от его среднего значения для i-го уровня фактора, т.е. 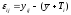или .

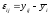В регрессионной модели обычно 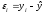, но так как фиктивная переменная принимает только два значения, то .

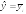Так, подставляя в наше уравнение z₁ = 1, z₂ = 0, получим 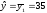для каждого завода первой группы по уровню автоматизации производства, что является для данной группы средней величиной (см.табл.3.9.5.). Соответственно, подставляя в уравнение регрессии z₁ = 0, z₂ = 1, получим: .

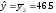В виду того, что теоретическое значение результативного признака в рассматриваемой модели представляют собой групповые средние (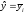), общая сумма квадратов отклонений 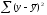раскладывается на одни и те же составляющие, как в регрессионном, так и в дисперсионном анализе по результатам группировки. Так, для дисперсионного анализа имеем:

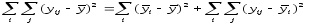
Общая сумма квадратов

Факторная сумма квадратов

Остаточная сумма квадратов

Для регрессионной модели данное балансовое равенство примет следующий вид:

.

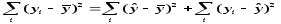Общая сумма квадратов

Факторная сумма квадратов

Остаточная сумма квадратов

Но так как 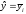, то факторная и остаточная суммы квадратов, найденные по регрессионной модели и по модели дисперсионного анализа совпадают (см.табл.3.6.).

Таблица 3.6.