
- •Коэффициент эластичности
- •Обобщенный метод наименьших квадратов.
- •Регрессионные модели с переменной структурой
- •X1, x2,…, xk – экономические переменные.
- •Распространенность ручного труда на предприятиях одной отрасли в зависимости от уровня автоматизации производства.
- •Результаты однофакторного дисперсионного анализа (двухфакторной регрессионной модели с фиктивными переменными).
- •Зависимость расходов на антиквариат от доходов условных денежных единиц
- •77 См. Например, г. Аптон. Анализ таблиц сопряженности. Перевод с англ. М.: Статистика, 1982.
Регрессионные модели с переменной структурой
До сих пор в качестве факторов рассматривались экономические переменные, принимающие количественные значения в некотором интервале. Вместе с тем, может оказаться необходимым включить в модель фактор, имеющий два или более качественных уровня. Это могут быть разного рода атрибутивные признаки, такие, например, как профессия, пол, образование, климатические условия, отдельные регионы. Чтобы ввести такие переменные в регрессионную модель, они должны быть упорядочены и им присвоены те или иные значения, т.е. качественные переменные преобразованы в количественные. Такого вида сконструированные переменные принято в эконометрике называть фиктивными переменными. В отечественной литературе за ними закрепился термин структурные переменные.
Качественные признаки могут приводить к неоднородности исследуемой совокупности, что может быть учтено при моделировании двумя путями:
- регрессия строится для каждой качественно отличной группы единиц совокупности, т.е. для каждой группы в отдельности, чтобы преодолеть неоднородность единиц общей совокупности;
- построение общей регрессионной модели для совокупности в целом, учитывающей неоднородность данных. В этом случае в регрессионную модель вводятся фиктивные переменные, т.е. строится регрессионная модель с переменной структурой, отражающей неоднородность данных.
Рассмотрим применение фиктивных переменных для функции спроса. Предположим, что по группе лиц мужского и женского пола изучается линейная зависимость потребления кофе от цены. В общем виде для совокупности обследуемых уравнение регрессии имеет вид:
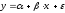 ,
,
где: y - количество потребляемого кофе,
x - цена.
Аналогичные
уравнения могут быть найдены отдельно
для лиц мужского
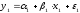 и женского пола:
и женского пола:
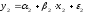 .
.
Различия в
потреблении кофе проявятся в различии
средних
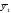 и
и 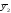 .
Вместе с тем, сила влияния x
на y
может быть одинаковой, т.е.
.
Вместе с тем, сила влияния x
на y
может быть одинаковой, т.е.
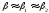 .
В этом случае возможно построение общего
уравнения регрессии с включением в него
фактора «пол» в виде фиктивной переменной.
Объединяя уравнения y1
и y2
и вводя фиктивные переменные, можно
придти к следующему соотношению:
.
В этом случае возможно построение общего
уравнения регрессии с включением в него
фактора «пол» в виде фиктивной переменной.
Объединяя уравнения y1
и y2
и вводя фиктивные переменные, можно
придти к следующему соотношению:
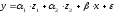 ,
,
где: z1 и z2 фиктивные переменные, принимающие значения:
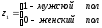 ;
;
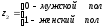 .
.
В общем уравнении регрессии зависимая переменная y рассматривается как функция не только цены x, но и пола (z1 , z2). Переменная z рассматривается как дихотомическая переменная, принимающая всего два значения: 1 и 0. При этом, когда z1 = 1, то z2 =0 и, наоборот, при z1 = 0 переменная z2 = 1.
Для лиц мужского
пола, когда z1 = 1 и z2
= 0, объединенное уравнение регрессии
составит:
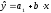 ,
а для лиц женского пола, когда z1
= 0 и z2 = 1,
,
а для лиц женского пола, когда z1
= 0 и z2 = 1,
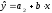 .
Иными словами, различия в потреблении
для лиц мужского и женского пола вызваны
различиями свободных членов уравнения
регрессии:
.
Иными словами, различия в потреблении
для лиц мужского и женского пола вызваны
различиями свободных членов уравнения
регрессии:
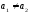 .
Параметр b является общим для всей
совокупности лиц, как для мужчин, так и
для женщин.
.
Параметр b является общим для всей
совокупности лиц, как для мужчин, так и
для женщин.
Вместе с тем, при
практическом введении фиктивных
переменных z1
и z2
в модель
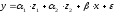 применение МНК для оценивания параметров
α1
и α2,
приведет к вырожденной матрице исходных
данных, а, следовательно, и к невозможности
получения их оценок. Объясняется это
тем, что при использовании МНК для
данного уравнения появляется свободный
член, т.е. уравнение примет вид:
применение МНК для оценивания параметров
α1
и α2,
приведет к вырожденной матрице исходных
данных, а, следовательно, и к невозможности
получения их оценок. Объясняется это
тем, что при использовании МНК для
данного уравнения появляется свободный
член, т.е. уравнение примет вид:
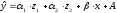 .
.
Предполагая при параметре A независимую переменную 1, имеем матрицу исходных факторов:
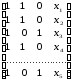 .
.
В рассматриваемой матрице существует линейная зависимость между первым, вторым и третьим столбцами: первый равен сумме второго и третьего. Поэтому матрица исходных факторов вырождена. Выходом из создавшегося затруднения может явиться переход к уравнениям вида:
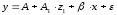 или
или
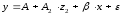 ,
,
каждое из которых включает только одну фиктивную переменную: z1 или z2.
Предположим, что
определено уравнение
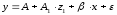 ,
,
где: z1 - принимает значения 1 для мужчин и 0 для женщин. Теоретические значения размера потребления кофе для мужчин окажутся равными:
 .
.
Для женщин соответствующие значения получим из выражения:
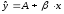 .
.
Сопоставляя эти результаты, видим, что различия в уровне потребления мужчин и женщин состоят в различии свободных членов данных уравнений: A - для женщин и A + A1 для мужчин.
Примером использования фиктивных переменных может служить зависимость урожайности пшеницы y от вида вспашки z и количества внесенного органического удобрения x. По 25 наблюдениям парное уравнение регрессии (без учета вида вспашки) составило:
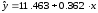 ;
;
F = 8,7; tА = 11,9; tβ = 2,95; ryx = 0,5246.
При его расчете использовалась следующая система нормальных уравнений:
 .
.
Уравнение регрессии статистически значимо: F, tb, ryx превышают табличные значения (при 5 %-ом уровне существенности и числе степеней свободы 23: F = 4,28; tb = 2,069; ryx = 0,398; при 1%-ой вероятности ошибки: F = 7,88; tb = 2,807; ryx = 0,507;).
По виду вспашки
поля характеризовались двумя категориями:
зяблевая и весенняя. Вид вспашки не
влияет на количество внесенных удобрений,
но обусловливает различия в урожайности.
Чтобы убедиться в этом введем в уравнение
регрессии фиктивную переменную z
для отражения эффекта вида вспашки, а
именно: z =
1 для зяблевой вспашки и z
= 0 для весенней
вспашки. Уравнение регрессии примет
вид:
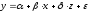 .
Применяя метод наименьших квадратов
для оценки параметров данного уравнения,
получим следующую систему нормальных
уравнений:
.
Применяя метод наименьших квадратов
для оценки параметров данного уравнения,
получим следующую систему нормальных
уравнений:
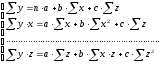
В виду того, что z
принимает лишь два значения (1 и 0),
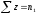 (число полей с зяблевой вспашкой),
(число полей с зяблевой вспашкой),
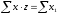 (количество внесенных удобрений на
полях с зяблевой вспашкой),
(количество внесенных удобрений на
полях с зяблевой вспашкой),
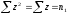 ,
,
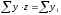 (сумма y
по полям зяблевой вспашки).
(сумма y
по полям зяблевой вспашки).
В рассматриваемом примере вся совокупность из 25 единиц подразделена на две подгруппы: с зяблевой вспашкой - 13 полей и с весенней - 12 полей, т.е. n1 = 13 и n2 = 12. Соответственно этим двум группам имеем:
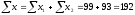 ;
;
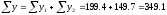 .
.
Тогда система нормальных уравнений примет вид:

Решая ее, получим уравнение регрессии:
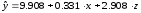
Уравнение регрессии
статистически значимо: F
= 15,6; R
= 0,766;
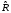 =
0,741; ta
= 11,8;
tb
= 3,9; tc
= 4,1. Как
видим, добавление в регрессию фиктивной
переменной существенно улучшило
результат модели: доля объясненной
вариации выросла с 27,5% (
=
0,741; ta
= 11,8;
tb
= 3,9; tc
= 4,1. Как
видим, добавление в регрессию фиктивной
переменной существенно улучшило
результат модели: доля объясненной
вариации выросла с 27,5% (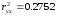 )
до 58,7% (
)
до 58,7% (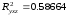 ).
При этом, сила влияния количества
внесенных органических удобрений на
урожайность осталась практически
неизменной: коэффициенты регрессии по
существу одинаковы (0,326 в парном уравнении
и 0,330 во множественном). Корреляция между
видом вспашки и количеством внесенного
удобрения на 1 га практически отсутствует:
).
При этом, сила влияния количества
внесенных органических удобрений на
урожайность осталась практически
неизменной: коэффициенты регрессии по
существу одинаковы (0,326 в парном уравнении
и 0,330 во множественном). Корреляция между
видом вспашки и количеством внесенного
удобрения на 1 га практически отсутствует: 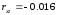 .
Вместе с тем, применение зяблевой вспашки
способствует росту урожайности в среднем
на 2,9 ц с 1 га при одном и том же количестве
внесенного удобрения на 1 га, что в целом
соответствует и различию средней
урожайности по видам вспашки (15,3 ц с 1
га для зяблевой вспашки и 12,5 ц с 1 га для
весенней вспашки). Частный F-критерий
для фактора z составил 16,58, что выше
табличного значения при числе степеней
свободы 1 и 22 (4,30 при α
= 0,05 и 7,94 при α
= 0,01). Это подтверждает целесообразность
включения фиктивной переменной в
уравнение регрессии.
.
Вместе с тем, применение зяблевой вспашки
способствует росту урожайности в среднем
на 2,9 ц с 1 га при одном и том же количестве
внесенного удобрения на 1 га, что в целом
соответствует и различию средней
урожайности по видам вспашки (15,3 ц с 1
га для зяблевой вспашки и 12,5 ц с 1 га для
весенней вспашки). Частный F-критерий
для фактора z составил 16,58, что выше
табличного значения при числе степеней
свободы 1 и 22 (4,30 при α
= 0,05 и 7,94 при α
= 0,01). Это подтверждает целесообразность
включения фиктивной переменной в
уравнение регрессии.
Парные уравнения регрессии по отдельным видам вспашки показывают, практически одинаковую меру влияния количества внесенного удобрения на урожайность:
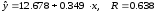 - при зяблевой
вспашке и
- при зяблевой
вспашке и
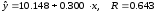 - при весенней
вспашке.
- при весенней
вспашке.
Поэтому вполне
реально предположить единую меру влияния
данного фактора не зависимо от вида
вспашки, что и имеет место в уравнении
регрессии с фиктивной переменной.
Включив фиктивную переменную, удалось
измерить ее влияние на изменение
урожайности: частный коэффициент
корреляции
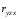 ,
оценивающий в чистом виде влияние
данного фактора, составил 0,6555, что
несколько выше, чем аналогичный показатель
для фактора x:
,
оценивающий в чистом виде влияние
данного фактора, составил 0,6555, что
несколько выше, чем аналогичный показатель
для фактора x:
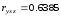 .
.
Частные уравнения регрессии по отдельным видам вспашки составили:
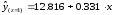 - для зяблевой
вспашки
- для зяблевой
вспашки
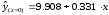 - для весенней
вспашки.
- для весенней
вспашки.
Как видим, функция урожайности для первой группы (при z = 1) параллельно сдвинута вверх.
В рассмотренном примере качественный фактор имел только два состояния, которым и соответствовали обозначения 1 и 0. Если же число градаций качественного признака-фактора превышает два, то в модель вводится несколько фиктивных переменных, число которых должно быть меньше числа качественных градаций. Только при соблюдении этого положения матрица исходных фиктивных переменных не будет линейно зависима и возможна оценка параметров модели.
Например, при изучении зависимости цены двухкомнатной квартиры от ее полезной площади в модель могут быть введены фиктивные переменные, отражающие тип дома: «хрущевка», панельный, кирпичный. При использовании трех категорий домов вводятся две фиктивные переменные: z1 и z2. Пусть переменная z1 принимает значение 1 для панельного типа дома, и 0 для всех остальных типов домов; переменная z2 принимает значение 1 для кирпичных домов, и 0 для остальных; тогда переменные z1 и z2 принимают нулевые значения для «хрущевки».
Предположим, что уравнение регрессии с фиктивными переменными составило:
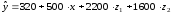 .
.
Частные уравнения регрессии для отдельных типов домов будут иметь вид:
-
«хрущевки» -
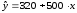 ;
; -
панельные -
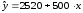 ;
; -
кирпичные -
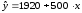 ;
;
демонстрируя наиболее высокие цены для квартир в панельных домах.
Параметры при фиктивных переменных z1 и z2 представляют собой разность между средним уровнем результативного признака для соответствующей группы и базовой группы. В рассматриваемом примере за базу сравнения цены взяты дома «хрущевки», для которых z1 = z2 = 0. Параметр при z1 = 2200 означает, что при одной и той же полезной площади квартиры цена ее в панельных домах в среднем на 2200 долларов США выше, чем в «хрущевках». Соответственно, параметр при z2 показывает, что в кирпичных домах цена выше в среднем на 1600 долларов при неизменной величине полезной площади по сравнению с указанным типом домов.
Рассмотренная трактовка параметров регрессии при фиктивных переменных справедлива, если сила влияния на «у» фактора «х» действительно не меняется в разных структурных частях совокупности. Иными словами, отсутствует взаимодействие факторов х; и фиктивных переменных z, т.е. для каждого значения z влияние х на у одинаково, что соответствует графику:
у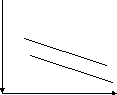
(при z = 1)
4 (при z = 0)
2
5 10 х
Целесообразность построения модели:
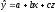
При наличии взаимодействия факторов (х и z) модель с фиктивной переменной принимает вид:
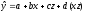 ,
что соответствует графическому
изображению:
,
что соответствует графическому
изображению:
у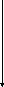
(при
z
= 1)

4 (при z = 0)
2
5 10 х
Наличие взаимодействия
факторов обусловливает модель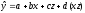 .
.
Предположим рассматриваются две группы наблюдений, для каждой из которых имеет место функциональная зависимость у от х:
уI
= 20 + 5x;
τух
= 1;
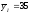 ;
;
уII
= 70 –
3х;
τух
= 1;
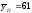 .
.
Поскольку на лицо четкое взаимодействие факторов, то попытка построить общую регрессионную модель вида у = а + вх + сz приведет к ухудшению результатов аппроксимации модели:
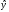 =
58 + 1х – 26zR2
= 0,842
=
58 + 1х – 26zR2
= 0,842
Верной в ней будет
лишь трактовка коэффициента регрессии
при фиктивной переменной z.
Поскольку в модели z
= 1 для I
группы наблюдений, когда
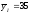 ,
а z
= 0 для П-ой
группы наблюдений, когда
,
а z
= 0 для П-ой
группы наблюдений, когда
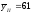 ,
то параметр при z,
равный: - 26, означает, что
,
то параметр при z,
равный: - 26, означает, что
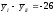 .
.
Модель с учетом взаимодействия факторов составит:
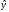 = 70 – 3х – 50z
+ 8(zx)
R2
= 1,
= 70 – 3х – 50z
+ 8(zx)
R2
= 1,
т.е. функциональная зависимость, заложенная в информацию для каждой группы, продолжает действовать. При z = 0 мы получим уравнение связи для второй группы, т.е. уII = 70 – 3х. Параметр с при z показывает различие в параметрах а для двух сравниваемых групп: с = аI – аII = -50. Параметр d при совмещенной переменной (zx) фиксирует различие в силе связи у и х в группах:
d = bI – bII = 5 – (-3) = 8
В отдельных случаях может оказаться необходимым введение двух и более групп фиктивных переменных, т.е. двух и более качественных факторов, каждый из которых может иметь несколько градаций. Например, при изучении потребления некоторого товара, наряду с факторами, имеющими количественное выражение (цена, доход на одного члена семьи, цена на взаимозаменяемые товары и др.), учитываются и качественные факторы. С их помощью оцениваются различия в потреблении отдельных социальных групп населения, дифференциация в потреблении по полу, национальному составу и др. При построении такой модели из каждой группы фиктивных переменных следует исключить по одной переменной. Так, если модель будет включать три социальные группы, три возрастные категории и ряд экономических переменных, то она примет вид:
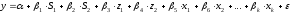
где: y - потребление,
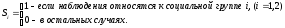 ;
;
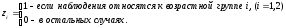 ;
;
