Налоговая_база / Налоговая база региона (теория) / Билет 17

Билет 17

КРИВАЯ ГОМПЕРЦА

Это часто используемая кривая роста. Названа она в честь Бенджамина Гомперца (1799—1865), английского статистика и математика, который первым предложил эту кривую как закон поведения уровней смертности. Было установлено, что она описывает также и распределение дохода.

Уравнением кривой Гомперца будет

Как и кривая Перла, кривая Гомперца простирается от нуля при t, равном минус бесконечности, до верхнего предела L при t, равном плюс бесконечности. Кривая, однако, несимметрична. Точка перегиба приходится на

На рис. показана кривая Гомперца, у которой L, b и k равны единице. При подгонке кривой Гомперца к совокупности данных мы сталкиваемся с той же проблемой, что и в случае с кривой Перла. Если мы попытаемся минимизировать сумму квадратов разностей между значениями ординат кривой Гомперца и нашими данными, то получим трансцендентное уравнение, которое в замкнутой форме неразрешимо. Поэтому используем в основном такой же подход, как в предыдущем разделе. Преобразуем уравнение (4-2) следующим образом:

Заметим, что L/y всегда больше единицы, следовательно, ln (L/y} всегда положителен, и операция с левой частью уравнения (4-6) всегда легко осуществима.

После того как верхний предел определен и данные преобразованы так, как показано в левой части уравнения (4-6), примем

и найдем k и b, минимизируя

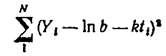
для нахождения регрессии для Y на t. Свободным членом уравнения регрессии является ln b, а коэффициентом регрессии — k (заметим, что k — положительное число, а коэффициент регрессии здесь всегда будет иметь отрицательный знак, поэтому он равен k со знаком минус).

Как и в случае с кривой Перла, согласно этому методу минимизируется квадрат функции отношений между ординатами выравнивающей кривой и исходными данными, а не квадратов разностей между значениями ординат выравнивающей кривой и данными. Тем не менее, этот метод легок в обращении, удобен на практике и, следовательно, удовлетворяет как инструмент прогнозирования.

Некоторые вычислительные центры имеют также программы, которые используют итеративные методы для выравнивания по кривой Гомперца. Если имеется одна из таких программ, проще использовать ее, а не метод, описанный выше