Кристаллография / kristalka

Тригонтритетраэдр

Тетрагонтритетраэдр

Пентагонтритетраэдр

Гесатетраэдр

Октааэдр

Тригонтриоктаэдр

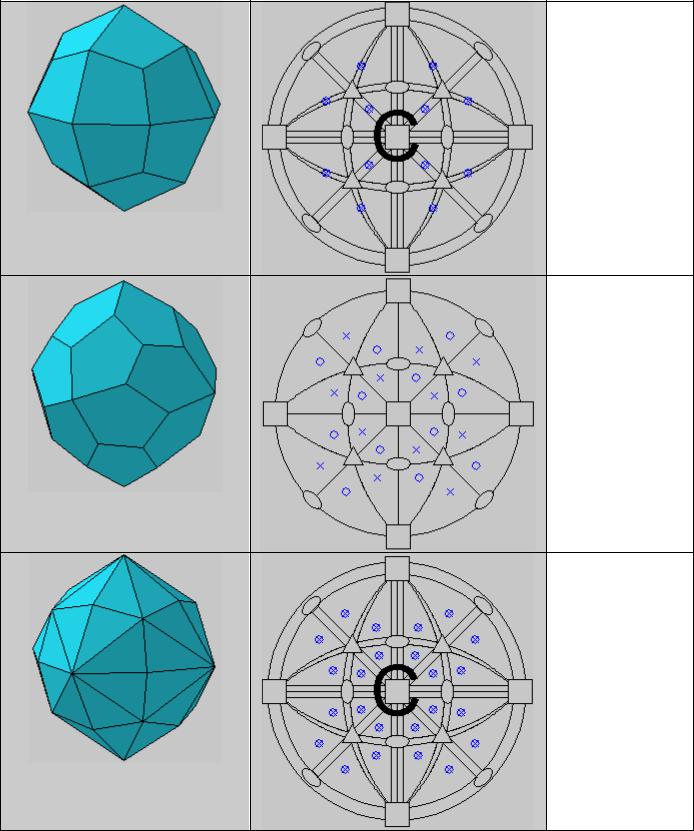
Тетрагонтриоктаэдр

Пентагонтриоктаэдр

Гесоктаэдр

Куб (гексаэдр)

Тетрагексаэдр

Ромбо-додекаэдр

Пентагон-додекаэдр

Дидодекаэдр

Огранка реального кристалла является более сложной, поскольку скорость роста тех или иных граней определяется, кроме их физических свойств, внешними условиями. При этом эквивалентные грани могут оказаться различными по геометрическим размерам, а в кристалле одновременно проявляются грани, входящие в различные правильные системы. Возможны также ситуации, когда несвязанные элементами симметрии грани имеют одинаковые свойства роста.

Категории

Разбиение кристаллов по категориям основано на возможности выделения единичных направлений. Единичным

направлением называется такое направление, которое преобразуется само в себя при действии всех элементов симметрии данного класса. Чем меньше единичных направлений в кристалле, тем более он симметричен. Возможны следующие случаи

•В кристаллах, в которых возможно выделение нескольких единичных направлений, относят к низшей категории. Такие кристаллы обладают наиболее ярко выраженной анизотропией свойств.

•В кристаллах, в которых существует единственное единичное направление, относят к средней категории. В таких кристаллах свойства вдоль единичного направления обычно сильно отличаются от свойств во всех других направлениях.

•И, наконец, кристаллы, в которых нет единичных направлений, относят к высшей категории. Свойства таких кристаллов близки к изотропным.

Для того, чтобы элемент симметрии – поворотная или инверсионная ось - не действовал на некоторое направление, необходимо, чтобы этот элемент симметрии был либо совпадал с этим направлением, либо являлся перпендикулярной к направлению осью симметрии второго порядка (возможно, инверсионной). Этот принцип позволяет легко разделить классы симметрии по категориям

Вкристаллах, не содержащих элементов симметрии или содержащих только центр симметрии, любое направление является единичным. Такие кристаллы принадлежат к низшей категории

Вкристаллах, обладающих только одной осью второго порядка (возможно, инверсионной), единичными направлениями являются направления вдоль оси и перпендикулярно к ней. Эти кристаллы принадлежат к низшей категории.

Вкристаллах, обладающих только тремя осями второго порядка (возможно, инверсионными), направления вдоль взаимно перпендикулярных осей симметрии переходят сами в себя. Таким образом, в этих кристаллах находится три единичных направления, и они также принадлежат к низшей категории.

Вкристаллах, обладающих одной осью симметрии третьего, четвертого или шестого порядка, только направление вдоль оси является единичным. Таким образом, эти кристаллы относятся к средней категории.

Во всех остальных кристаллах есть несколько осей порядка выше второго, действие которых не позволяет появиться единичному направлению. Такие кристаллы будут относиться к высшей категории.

Кристаллические системы

Распределение кристаллов по кристаллическим системам основано на выделении общих, одинаковых по типу и расположению, элементов симметрии. Эти элементы симметрии называют определяющими элементами симметрии. Всего возможно семь кристаллических систем

1. В кристаллах триклинной системы может не быть ни одного элемента симметрии (ось первого порядка) или быть только центр симметрии (инверсионная ось первого порядка).

2.В кристаллах моноклинной системы может быть только одна ось второго порядка, возможно, инверсионная (плоскость симметрии).

3.В ромбических кристаллах должны быть три оси второго порядка, возможно, инверсионных.

4.В тригональных кристаллах должна быть одна ось третьего порядка, возможно, инверсионная.

5.В тетрагональных кристаллах должна быть одна ось четвертого порядка, возможно, инверсионная.

6.В гексагональных кристаллах должна быть одна ось шестого порядка, возможно, инверсионная.

7.В кубических кристаллах должно быть четыре оси третьего порядка.

Всоответствии с приведенным выше анализом возможных элементов симметрии в кристаллах различных категорий, можно сделать вывод о том, что

книзшей категории принадлежат кристаллы триклинной, моноклинной и ромбической системы;

ксредней – кристаллы тригональной, тетрагональной и гексагональной системы;

квысшей – кристаллы кубической системы.

Правила установки

Существенно, что в кристаллографии направление координатных осей по возможности связывается с элементами симметрии. Правила, по которым выбираются координатные оси, называются правилами установки.

Втриклинной системе координатные оси невозможно связать с элементами симметрии, поэтому оси выбирают параллельно ребрам или перпендикулярно граням кристалла.

Вмоноклинной системе есть единственный элемент симметрии – ось второго порядка (возможно, инверсионная), параллельно ей направляют ось Y. Оси X и Z направляют вдоль ребер или перпендикулярно граням кристалла в плоскости, перпендикулярной оси Y.

Вромбической системе обязательно присутствуют три оси второго порядка (возможно, инверсионные), параллельно им направляют оси X, Y, Z.

Вкристаллах средней категории ось Z направляют вдоль выделенной оси (третьего, четвертого или шестого

порядка), а оси X и Y перпендикулярно оси Z так, что в тригональной и гексагональной системе угол между ними равен 120о, а в тетрагональной - 90 о. Очевидно, оси X и Y эквивалентны друг другу. Направление осей X и Y выбирают вдоль осей симметрии второго порядка, при их отсутствии – перпендикулярно плоскостям симметрии, при их отсутствии – параллельно ребрам и перпендикулярно граням кристалла.

Вкристаллах кубической системы обязательно существуют четыре оси третьего порядка, оси X,Y и Z направляют равнонаклонно к ним. В этих направлениях в кубических кристаллах проходят оси второго или четвертого порядка.

Выбор координатных осей задает сингонию кристалла. Так как в тригональной и гексагональной системах выбор координатных осей одинаков, они входят в одну – гексагональную – сингонию.

Главные направления

Из-за того, что направления координатных осей связаны с элементами симметрии, элементы симметрии могут находиться только в строго определенных кристаллографических направлениях. Для каждой кристаллической системы определены от одного до трех главных направления, называемых главными направлениями, в которых могут располагаться элементы симметрии.

Главные трансляционные направления в кристаллах различной симметрии.

Правила записи символов Германа-Могена класса симметрии

Главные направления используют при записи классов симметрии в символике Германа-Могена. Выделяют три позиции записи, в каждой из которых последовательно записывают ось симметрии, идущую вдоль каждого главного направления. Если перпендикулярно к этому направлению проходит плоскость симметрии. то элемент симметрии записывают в виде дроби: в числителе – ось, в знаменателе – плоскость симметрии.